1.3. Inflation and perturbations

A complete description of the Universe should include a description of deviations from homogeneity, at least in a statistical way. Indeed, some of the most powerful probes of the parameters described above come from studying the evolution of perturbations, so their study is naturally intertwined in the determination of cosmological parameters.

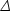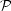There are many different notations used to describe the perturbations, both in terms of the quantity used to describe the perturbations and the definition of the statistical measure. We use the dimensionless power spectrum ² as defined in Olive and Peacock (also denoted in some of the literature). If the perturbations obey Gaussian statistics, the power spectrum provides a complete description of their properties.

From a theoretical perspective, a useful quantity to describe the perturbations is the curvature perturbation , which measures the spatial curvature of a comoving slicing of the space-time. A case of particular interest is the Harrison-Zel'dovich spectrum, which corresponds to a constant spectrum 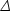². More generally, one can approximate the spectrum by a power-law, writing

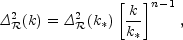
(1.3)

where n is known as the spectral index, always defined so that n = 1 for the Harrison-Zel'dovich spectrum, and k_* is an arbitrarily chosen scale. The initial spectrum, defined at some early epoch of the Universe's history, is usually taken to have a simple form such as this power-law, and we will see that observations require n close to one, which corresponds to the perturbations in the curvature being independent of scale. Subsequent evolution will modify the spectrum from its initial form.

The simplest viable mechanism for generating the observed perturbations is the inflationary cosmology, which posits a period of accelerated expansion in the Universe's early stages [4]. It is a useful working hypothesis that this is the sole mechanism for generating perturbations. Commonly, it is further assumed to be the simplest class of inflationary model, where the dynamics are equivalent to that of a single scalar field slowly rolling on a potential V(). One aim of cosmology is to verify that this simple picture can match observations, and to determine the properties of V() from the observational data.

Inflation generates perturbations through the amplification of quantum fluctuations, which are stretched to astrophysical scales by the rapid expansion. The simplest models generate two types, density perturbations which come from fluctuations in the scalar field and its corresponding scalar metric perturbation, and gravitational waves which are tensor metric fluctuations. The former experience gravitational instability and lead to structure formation, while the latter can influence the cosmic microwave background anisotropies. Defining slow-roll parameters, with primes indicating derivatives with respect to the scalar field, as

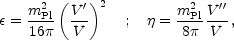
(1.4)

which should satisfy , || << 1, the spectra can be computed using the slow-roll approximation as

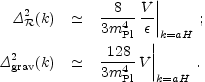
(1.5)

In each case, the expressions on the right-hand side are to be evaluated when the scale k is equal to the Hubble radius during inflation. The symbol `' indicates use of the slow-roll approximation, which is expected to be accurate to a few percent or better.

From these expressions, we can compute the spectral indices

(1.6)

Another useful quantity is the ratio of the two spectra, defined by

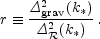
(1.7)

The literature contains a number of definitions of r; this convention matches that of recent versions of CMBFAST [5] and of WMAP [6], while definitions based on the relative effect on the microwave background anisotropies typically differ by tens of percent. We have

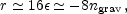
(1.8)

which is known as the consistency equation.

In general one could consider corrections to the power-law approximation, and indeed WMAP found some low-significance evidence that this might be needed, which we discuss later. However for now we make the working assumption that the spectra can be approximated by power laws. The consistency equation shows that r and n_grav are not independent parameters, and so the simplest inflation models give initial conditions described by three parameters, usually taken as 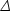², n, and r, all to be evaluated at some scale k_*, usually the `statistical centre' of the range explored by the data. Alternatively, one could use the parametrization V, , and , all evaluated at a point on the putative inflationary potential.

After the perturbations are created in the early Universe, they undergo a complex evolution up until the time they are observed in the present Universe. While the perturbations are small, this can be accurately followed using a linear theory numerical code such as CMBFAST [5]. This works right up to the present for the cosmic microwave background, but for density perturbations on small scales non-linear evolution is important and can be addressed by a variety of semi-analytical and numerical techniques. However the analysis is made, the outcome of the evolution is in principle determined by the cosmological model, and by the parameters describing the initial perturbations, and hence can be used to determine them.

Of particular interest are cosmic microwave background anisotropies. Both the total intensity and two independent polarization modes are predicted to have anisotropies. These can be described by the radiation angular power spectra C as defined in the article of Scott and Smoot in this volume, and again provide a complete description if the density perturbations are Gaussian.