1.2. Neutrinos

The standard neutrino sector has three flavors. For neutrinos of mass in the range 5 × 10^-4 eV to 1 MeV, the density parameter in neutrinos is predicted to be

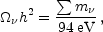
(1.2)

where the sum is over all families with mass in that range (higher masses need a more sophisticated calculation). We use units with c = 1 throughout. Recent results on atmospheric and solar neutrino oscillations [2] imply non-zero mass-squared differences between the three neutrino flavors. These oscillation experiments cannot tell us the absolute neutrino masses, but within the simple assumption of a mass hierarchy suggest a lower limit of 0.001 on the neutrino mass density parameter.

For a total mass as small as 0.1 eV, this could have a potentially observable effect on the formation of structure, as neutrino free-streaming damps the growth of perturbations. Present cosmological observations have shown no convincing evidence of any effects from either neutrino masses or an otherwise non-standard neutrino sector, and impose quite stringent limits, which we summarize in Section 3.4. Consequently, the standard assumption at present is that the masses are too small to have a significant cosmological impact, but this may change in the near future.

The cosmological effect of neutrinos can also be modified if the neutrinos have decay channels, or if there is a large asymmetry in the lepton sector manifested as a different number density of neutrinos versus anti-neutrinos. This latter effect would need to be of order unity to be significant, rather than the 10^-9 seen in the baryon sector, which may be in conflict with nucleosynthesis [3].