3.2. Supernovae as cosmological probes
The relation between observed flux and the intrinsic luminosity of an object depends on the luminosity distance dL, which in turn depends on cosmological parameters. More specifically
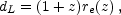
| (1.10) |
where re(z) is the coordinate distance. For example, in a flat Universe
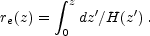
| (1.11) |
For a general dark energy equation of state
w(z) = pQ(z) /
Q(z),
the Hubble parameter is, still considering only the flat case,
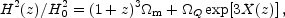
| (1.12) |
where
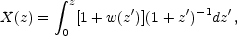
| (1.13) |
and 
m and
Q are the
present density parameters of matter and dark energy components.
If a general equation of state is allowed, then
one has to solve for w(z) (parameterized, for example, as
w(z) = w = constant, or
w(z) = w0 + w1z)
as well as for
Q.
Empirically, the peak luminosity of supernova of Type Ia (SNe Ia) can be used as an efficient distance indicator (e.g., Ref. [14]). The favorite theoretical explanation for SNe Ia is the thermonuclear disruption of carbon-oxygen white dwarfs. Although not perfect `standard candles', it has been demonstrated that by correcting for a relation between the light curve shape and the luminosity at maximum brightness, the dispersion of the measured luminosities can be greatly reduced. There are several possible systematic effects which may affect the accuracy of the SNe Ia as distance indicators, for example, evolution with redshift and interstellar extinction in the host galaxy and in the Milky Way, but there is no indication that any of these effects are significant for the cosmological constraints.
Two major studies, the `Supernova Cosmology Project' and the `High-z
Supernova Search Team', found evidence for an accelerating
Universe [15],
interpreted as
due to a cosmological constant, or to a more general `dark energy'
component. Recent results obtained by Tonry et al.
[16] are shown in
Figure 1 (see also Ref.
[17]).
The SNe Ia data alone can only constrain a combination of
m and
. When combined with the CMB data
(which indicates flatness, i.e.,
m +
1), the best-fit
values are
m
0.3 and
0.7.
Future experiments will aim to set constraints on the cosmic equation of
state w(z). However, given the integral relation between
the luminosity distance and w(z), it is not
straightforward to recover w(z)
(e.g., Ref. [18]).
 |
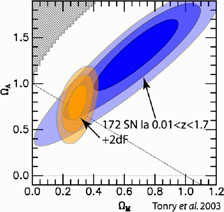Figure 1. This shows the preferred region in
the |