


3.3. Cosmic microwave background
The physics of the cosmic microwave background (CMB) is described in detail by Scott and Smoot in this volume. Before recombination, the baryons and photons are tightly coupled, and the perturbations oscillate in the potential wells generated primarily by the dark matter perturbations. After decoupling, the baryons are free to collapse into those potential wells. The CMB carries a record of conditions at the time of decoupling, often called primary anisotropies. In addition, it is affected by various processes as it propagates towards us, including the effect of a time-varying gravitational potential (the integrated Sachs-Wolfe effect), gravitational lensing, and scattering from ionized gas at low redshift.
The primary anisotropies, the integrated Sachs-Wolfe effect, and scattering from a homogeneous distribution of ionized gas, can all be calculated using linear perturbation theory, a widely-used implementation being the CMBFAST code of Seljak and Zaldarriaga [5]. Gravitational lensing is also calculated in this code. Secondary effects such as inhomogeneities in the re-ionization process, and scattering from gravitationally-collapsed gas (the Sunyaev-Zel'dovich effect), require more complicated, and more uncertain, calculations.
The upshot is that the detailed pattern of anisotropies, quantified, for
instance, by the angular power spectrum
C , depends on
all of the cosmological parameters. In a typical cosmology, the
anisotropy power spectrum [usually plotted as
, depends on
all of the cosmological parameters. In a typical cosmology, the
anisotropy power spectrum [usually plotted as
 (
( + 1)
C
+ 1)
C ] features a flat plateau at large angular scales (small
] features a flat plateau at large angular scales (small
 ), followed by a series of
oscillatory features at higher angular scales, the first and most prominent
being at around one degree (
), followed by a series of
oscillatory features at higher angular scales, the first and most prominent
being at around one degree (
 200). These features,
known as acoustic peaks, represent the oscillations of the photon-baryon
fluid around
the time of decoupling. Some features can be closely related to specific
parameters - for instance, the location of the first peak probes the
spatial geometry, while the relative heights of the peaks probes the baryon
density - but many other parameters combine to determine the overall shape.
200). These features,
known as acoustic peaks, represent the oscillations of the photon-baryon
fluid around
the time of decoupling. Some features can be closely related to specific
parameters - for instance, the location of the first peak probes the
spatial geometry, while the relative heights of the peaks probes the baryon
density - but many other parameters combine to determine the overall shape.
The WMAP experiment [1]
has provided the most accurate results to
date on the spectrum of CMB fluctuations
[19], with a precision
determination of the temperature power spectrum up to

 900, shown in
Figure 2,
and the first detailed measurement of the
correlation spectrum between temperature and polarization
[20] (the
correlation having first been detected by DASI
[21]). These
are consistent
with models based on the parameters we have described, and provide quite
accurate determinations of many of them
[7].
In this subsection,
we will refer to results from WMAP alone, with the following section
combining those with other observations. We note that as the parameter
fitting is done in a multi-parameter space,
one has to assume a `prior' range for each of the parameters
(e.g., Hubble constant 0.5 < h < 1), and there may be some
dependence on these assumed priors.
900, shown in
Figure 2,
and the first detailed measurement of the
correlation spectrum between temperature and polarization
[20] (the
correlation having first been detected by DASI
[21]). These
are consistent
with models based on the parameters we have described, and provide quite
accurate determinations of many of them
[7].
In this subsection,
we will refer to results from WMAP alone, with the following section
combining those with other observations. We note that as the parameter
fitting is done in a multi-parameter space,
one has to assume a `prior' range for each of the parameters
(e.g., Hubble constant 0.5 < h < 1), and there may be some
dependence on these assumed priors.
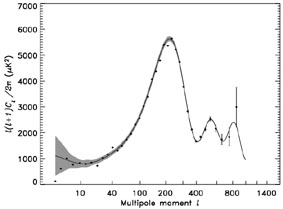 |
Figure 2. The angular power spectrum of the
cosmic microwave background as
measured by the WMAP satellite. The solid line shows the prediction from
the best-fitting
|
WMAP provides an exquisite measurement of the location of the first
acoustic peak, which directly probes the spatial geometry and yields a
total density
 tot
tot

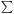
 i +
i +

 of
of
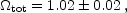
| (1.14) |
consistent with spatial flatness and completely excluding significantly
curved Universes (this result does however assume a fairly strong prior
on the Hubble parameter from other measurements; WMAP alone constrains
it only weakly, and
allows significantly closed Universes if h is small, e.g.
 tot = 1.3
for h = 0.3). It also gives a precision measurement of the age of
the Universe. It
gives a baryon density consistent with that coming from
nucleosynthesis, and affirms the need for both dark matter and dark
energy if the data are to be explained. For the spectral index of
density perturbations, WMAP alone is consistent with a power-law
spectrum, with spectral index n = 0.99 ± 0.04, and in
particular with a scale-invariant initial spectrum n = 1. It
shows no evidence for dynamics of the dark energy, being consistent with
a pure cosmological constant (w = - 1).
tot = 1.3
for h = 0.3). It also gives a precision measurement of the age of
the Universe. It
gives a baryon density consistent with that coming from
nucleosynthesis, and affirms the need for both dark matter and dark
energy if the data are to be explained. For the spectral index of
density perturbations, WMAP alone is consistent with a power-law
spectrum, with spectral index n = 0.99 ± 0.04, and in
particular with a scale-invariant initial spectrum n = 1. It
shows no evidence for dynamics of the dark energy, being consistent with
a pure cosmological constant (w = - 1).
One of the most interesting results, driven primarily by detection of
large-angle polarization-temperature correlations, is the discovery of a
high optical depth to re-ionization,
 ~ 0.17, which
roughly corresponds to a re-ionization redshift zion ~
17. This was higher than expected, though it appears it can be
accommodated in models for
development of the first structures which provide the ionizing flux.
~ 0.17, which
roughly corresponds to a re-ionization redshift zion ~
17. This was higher than expected, though it appears it can be
accommodated in models for
development of the first structures which provide the ionizing flux.
In addition to WMAP, useful information comes from measurements of the CMB on small angular scales by, amongst others, the ACBAR and CBI experiments. Further, in 2002 the DASI experiment made the first measurement of the polarization anisotropies [21], again consistent with the standard cosmology, though not with sufficient accuracy to provide detailed constraints.