3.4. Galaxy clustering

The power spectrum of density perturbations depends on the nature of the dark matter. Within the Cold Dark Matter model, the shape of the power spectrum depends primarily on the primordial power spectrum and on the combination _m h which determines the horizon scale at matter-radiation equality, with a subdominant dependence on the baryon density. The matter distribution is most easily probed by observing the galaxy distribution, but this must be done with care as the galaxies do not perfectly trace the dark matter distribution. Rather, they are a `biased' tracer of the dark matter. The need to allow for such bias is emphasized by the observation that different types of galaxies show bias with respect to each other. Further, the observed 3D galaxy distribution is in redshift space, i.e., the observed redshift is the sum of the Hubble expansion and the line-of-sight peculiar velocity, leading to linear and non-linear dynamical effects which also depend on the cosmological parameters. On the largest length scales, the galaxies are expected to trace the location of the dark matter, except for a constant multiplier b to the power spectrum, known as the linear bias parameter. On scales smaller than 20 h<sup>-1</sup> Mpc or so, the clustering pattern is `squashed' in the radial direction due to coherent infall, which depends on the parameter _m^0.6 / b (on these shorter scales, more complicated forms of biasing are not excluded by the data). On scales of a few h^-1 Mpc, there is an effect of elongation along the line of sight (colloquially known as the `finger of God' effect) which depends on the galaxy velocity dispersion _p.

3.4.1. The galaxy power spectrum

The 2-degree Field (2dF) Galaxy Redshift Survey is now complete and publicly available, with nearly 230,000 redshifts. ⁴ Analyses of a subset of the full data (containing 160,000 redshifts) measured the power spectrum for k > 0.02 h Mpc^-1 with ~ 10% accuracy, shown in Figure 3. The measured power spectrum is well fit by a CDM model with _m h = 0.18 ± 0.02, and a baryon fraction _b / _m = 0.17 ± 0.06 [22]. The pattern of the galaxy clustering in redshift space is fitted by = 0.49 ± 0.09 and velocity dispersion _p = 506 ± 52 km s^-1 [23]; note that the two are strongly correlated. Combination of the 2dF data with the CMB indicates b ~ 1, in agreement with a 2dF-alone analysis of higher-order clustering statistics. Results for these parameters also depend on the length scale over which a fit is done, and the selection of the objects by luminosity, spectral type, or color. In particular, on scales smaller than 10 h^-1 Mpc, different galaxy types are clustered differently. This `biasing' introduces a systematic effect on the determination of cosmological parameters from redshift surveys. Prior knowledge from simulations of galaxy formation could help, but is model-dependent. We note that the present-epoch power spectrum is not sensitive to dark energy, so it is mainly a probe of the matter density.

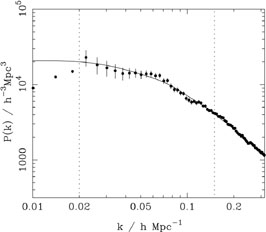Figure 3. The galaxy power spectrum from the 2dF galaxy redshift survey as derived in Ref. [22]. This plot shows P(k) 2(k) / k3, but with distances measured in redshift space and convolved with the survey geometry. The solid line shows a linear-theory CDM fit (also convolved with the survey geometry) with m h = 0.2, b / m = 0.15, h = 0.7 and n = 1. Only the range 0.02 h Mpc-1 < k < 0.15 h Mpc-1, where perturbations are in the linear regime, was used to obtain that best fit. The error bars are correlated, but with known covariances. [Figure provided by Will Percival; see also Ref. [22].

The Sloan Digital Sky Survey (SDSS) is a project to image a quarter of the sky, and to obtain spectra of galaxies and quasars selected from the imaging data. ⁵ A maximum likelihood analysis of early SDSS data by Szalay et al. [24] used the projected distribution of galaxies in a redshift bin around z = 0.33 to find _mh = 0.18 ± 0.04, assuming a flat CDM model with _m = 1 - = 0.3. The power spectrum of the latest version of SDSS redshift survey was published as this article was being finalized [25].

3.4.2. Limits on neutrino mass from 2dFGRS

Large-scale structure data can put an upper limit on the ratio / _m due to the neutrino `free streaming' effect [26]. By comparing the 2dF galaxy power spectrum with a four-component model (baryons, cold dark matter, a cosmological constant, and massive neutrinos), it was estimated that / _m < 0.13 (95% confidence limit), giving < 0.04 if a concordance prior of _m = 0.3 is imposed. The latter corresponds to an upper limit of about 2 eV on the total neutrino mass, assuming a prior of h 0.7 [27]. The above analysis assumes that the primordial power spectrum is adiabatic, scale-invariant and Gaussian. Potential systematic effects include biasing of the galaxy distribution and non-linearities of the power spectrum. Additional cosmological data sets bring down this upper limit by a factor of two [28]. The analysis of WMAP+2dFGRS [7] derived h² < 0.0067 (95% CL).

Laboratory limits on absolute neutrino masses from tritium beta decay and especially from neutrinoless double-beta decay should, within the next decade, push down towards (or perhaps even beyond) the 0.1 eV level that has cosmological significance.

⁴ See http://www.mso.anu.edu.au/2dFGRS. Back.

⁵ See http://www.sdss.org. Back.