


Most of the recent work on cosmological parameters has chosen a particular parameter set or sets, and investigated parameter constraints when faced with different observational datasets. However, the information criteria ask how well different models fit the same dataset. First we need to decide which models to consider.
A useful division of parameters is into those which are definitely
needed to give a reliable fit to the data, which I will call the base
parameter set, and those which have proved irrelevant, or of marginal
significance, in fits to the
present data. The base parameter set is actually extraordinarily small, and
given in Table 1. At present it seems that a
scale-invariant spectrum of adiabatic gaussian density perturbations,
requiring specification of just a single parameter (the amplitude), is
enough to give a good fit to the data. The
Universe can be taken as spatially-flat, with the dark matter, baryon, and
radiation densities requiring to be specified as independent
parameters. The base model includes a
cosmological constant/dark energy, whose density is fixed by the spatial
flatness condition. To complete the parameter set, we need the Hubble
constant. Accordingly, a minimal description of the Universe requires
just five fundamental parameters.
2
Further, the radiation density
 r
is directly measured at high accuracy from the cosmic microwave background
temperature and is not normally varied in fits to other data.
r
is directly measured at high accuracy from the cosmic microwave background
temperature and is not normally varied in fits to other data.
 m m |
matter density |
 b b |
baryon density |
 r r |
radiation density |
| h | hubble parameter |
| A | adiabatic density perturbation amplitude |
 |
reionization optical depth |
| b | bias parameter (or parameters) |
In addition to these fundamental parameters, comparisons with microwave
anisotropy and galaxy power spectrum data require knowledge of the
reionization optical depth  and the galaxy bias parameter b respectively. These are
not fundamental parameters, as they are in principle computable from the
above, but present understanding does not allow an accurate
first-principles derivation and instead typically they are taken as
additional phenomenological parameters to be fit from the data.
and the galaxy bias parameter b respectively. These are
not fundamental parameters, as they are in principle computable from the
above, but present understanding does not allow an accurate
first-principles derivation and instead typically they are taken as
additional phenomenological parameters to be fit from the data.
Complementary to this base parameter set is what I will call the list of candidate parameters. These are parameters which are not convincingly measured with present data, but some of which might be required by future data. Many of them are available in model prediction codes such as CMBFAST (Seljak & Zaldarriaga 1996). Cosmological observations seek to improve the measurement of the base parameters, and also to investigate whether better data requires the promotion of any parameters from the candidate set into the standard cosmological model. Table 2 shows a list of parameters which have already been discussed in the literature, and although already rather long is likely to be incomplete.
 k k |
spatial curvature |
N - 3.04 - 3.04 |
effective number of neutrino species (CMBFAST definition) |
m i i |
neutrino mass for species `i' |
| [or more complex neutrino properties] | |
| mdm | (warm) dark matter mass |
| w + 1 | dark energy equation of state |
| dw/dz | redshift dependence of w |
| [or more complex parametrization of dark energy evolution] | |
| cS2 - 1 | effects of dark energy sound speed |
| 1 / rtop | topological identification scale |
| [or more complex parametrization of non-trivial topology] | |
d / dz / dz |
redshift dependence of the fine structure constant |
| dG / dz | redshift dependence of the gravitational constant |
| n - 1 | scalar spectral index |
| dn / d ln k | running of the scalar spectral index |
| r | tensor-to-scalar ratio |
| r + 8nT | violation of the inflationary consistency equation |
| dnT / d ln k | running of the tensor spectral index |
| kcut | large-scale cut-off in the spectrum |
| Afeature | amplitude of spectral feature (peak, dip or step) ... |
| kfeature | ... and its scale |
| [or adiabatic power spectrum amplitude parametrized in N bins] | |
| fNL | quadratic contribution to primordial non-gaussianity |
| [or more complex parametrization of non-gaussianity] | |
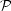 S S |
CDM isocurvature perturbation ... |
| nS | ... and its spectral index ... |
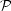 S S |
... and its correlation with adiabatic perturbations ... |
nS - nS - nS |
... and the spectral index of that correlation |
| [or more complicated multi-component isocurvature perturbation] | |
| Gµ | cosmic string component of perturbations |
The upper portion of Table 2 lists possible additional parameters associated with the background space-time, while the lower part contains those specifying the initial perturbations. The base cosmological model assumes these are all zero (as defined in the table), and indeed it is a perfectly plausible cosmological model that they are indeed all zero, with the sole exception of the neutrino masses, for which there is good non-cosmological evidence that they are non-zero. One should be fairly optimistic about learning something about neutrino masses from cosmology, which is why they are included as cosmological parameters. It is also possible that one day they might be pinned down accurately enough by other measurements that cosmologists no longer need to worry about varying them, and then neutrino masses will not be cosmological parameters any more than the electron or proton mass are.
It is of course highly unlikely that all the parameters on the candidate list will be relevant (if they were, observational data would have little chance of constraining anything), and on theoretical grounds some are thought much more likely than others. In most cases parameters can be added individually to the base model, but there are some dependences; for example, it doesn't make much sense to include spectral index running as a parameter unless the spectral index itself is included. Quite a lot of the parameters in Table 2 have now been added to a base parameter set (usually not the one I have adopted here, however) and compared to observational data. There is also the possibility that the simultaneous inclusion of two extra parameters, which are unrelated, might significantly improve the fit where neither parameter separately did. This is hard to fully test as there are so many possible combinations.
2 To be more precise, this base model
assumes all the parameters to be listed in
Table 2 are zero. Analyses may
use different parameter definitions equivalent to those given here, for
instance using the physical densities
 h2 in place of the density parameters.
Back.
h2 in place of the density parameters.
Back.