LMC Structure and Kinematics - R.P. van der Marel

4. ORBIT

To understand the tidal interactions in the Magellanic System it is important to know the orbit of the LMC around the Milky Way. This requires knowledge of all three of the velocity components of the LMC center of mass. The line-of-sight velocity can be accurately determined from the Doppler velocities of tracers (see Section 5). By contrast, determination of the velocity in the plane of the sky is much more difficult. For the LMC, proper motion determinations are available from the following sources: Kroupa et al. (1994), using stars from the PPM Catalogue; Jones, Klemola & Lin (1994), using photographic plates with a 14 year epoch span; Kroupa & Bastian (1997), using Hipparcos data; Drake et al. (2002), using data from the MACHO project; and Anguita, Loyola & Pedreros (2000) and Pedreros, Anguita & Maza (2002), using CCD frames with an 11 year epoch span. Some of the measurements pertain to fields in the outer parts in the LMC disk, and require corrections for the orientation and rotation of the LMC disk. The measurements are all more-or-less consistent with each other to within the error bars. The exception to this is the Anguita et al. result, which almost certainly suffers from an unidentified systematic error. When this latter result is ignored, the weighted average of the remaining measurements yields proper motions towards the West and North of (van der Marel et al. 2002)

(4.1)

Transformation of the proper motion to a space velocity in km s^-1 requires knowledge of the LMC distance D₀. Many techniques have been used over the years to estimate the LMC distance, but unfortunately, there continue to be systematic differences between the results from different techniques that far exceed the formal errors. It is beyond the scope of the present review to address this topic in detail. Instead, the reader is refered to the recent reviews by, e.g., Westerlund (1997), Gibson et al. (2000), Freedman et al. (2001) and Alves (2004b). Freedman et al. adopt a distance modulus m - M = 18.50 ± 0.10 on the basis of a review of all published work. This corresponds to D₀ = 50.1 ± 2.5 kpc. At this distance, a proper motion of 1 mas yr^-1 corresponds to 238 ± 12 km s^-1 and 1 degree on the sky corresponds to 0.875 ± 0.044 kpc.

Combination of the distance and proper motion of the LMC yields velocities v_W = - 399 km s^-1 and v_N = 80 km s^-1 towards the West and North, respectively, with errors of ~ 40 km s^-1 in each direction. This can be combined with the observed line-of-sight velocity, v_sys = 262.2 ± 3.4 km s^-1 (see Section 5.2), to obtain the three-dimensional motion of the LMC with respect to the Milky Way. It is usual to adopt a Cartesian coordinate system (X, Y, Z), with the origin at the Galactic Center, the Z-axis pointing towards the Galactic North Pole, the X-axis pointing in the direction from the sun to the Galactic Center, and the Y-axis pointing in the direction of the sun's Galactic Rotation. The observed LMC velocities must be corrected for the reflex motion of the sun, which is easily done with use of standard estimates for the position and velocity of the sun with respect to the Galactic center. The (X, Y, Z) position of the LMC is then found to be (van der Marel et al. 2002)

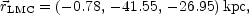(4.2)

and its three-dimensional space velocity is

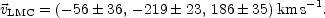(4.3)

This corresponds to a distance of 49.53 kpc from the Galactic center, and a total velocity of 293 ± 39 km s^-1 in the Galactocentric rest frame. The motion has a radial component of 84 ± 7 km s^-1 pointing away from the Galactic center, and a tangential component of 281 ± 41 km s^-1. The proper motion of the SMC is known only with errors of ~ 0.8 mas yr^-1 in each coordinate (Kroupa & Bastian 1997), which is five times less accurate than for the LMC. However, to within these errors the SMC is known to have a galactocentric velocity vector that agrees with that of the LMC.

The combination of a small but positive radial velocity and a tangential velocity that exceeds the circular velocity of the Milky Way halo implies that the LMC must be just past pericenter in its orbit. The calculation of an actual orbit requires knowledge of the three-dimensional shape and the radial profile of the gravitational potential of the Milky Way dark halo. Gardiner et al. (1994) and Gardiner & Noguchi (1996) calculated orbits in a spherical Milky Way halo potential with a rotation curve that stays flat at 220 km s^-1 out to a galactocentric distance of at least 200 kpc. Such a potential is consistent with our present understanding of the Milky Way dark halo (Kochanek 1996; Wilkinson & Evans 1999; Ibata et al. 2001). The calculations properly take into account that the LMC and SMC orbit each other while their center of mass orbits the Milky Way. However, since the LMC is more massive than the SMC, its motion is not too different from that of the LMC-SMC center of mass. For an assumed present-day LMC velocity 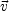vector{v} _LMC consistent with that given in equation (4.3) the apocenter to pericenter ratio is inferred to be ~ 2.5 : 1. The perigalactic distance is ~ 45 kpc and the orbital period around the Milky Way is ~ 1.5 Gyr.