5. KINEMATICS

The kinematical properties of the LMC provide important clues to its structure. Observations have therefore been obtained for many tracers. The kinematics of gas in the LMC have been studied primarily using HI (e.g., Rohlfs et al. 1984; Luks & Rohlfs 1992; Kim et al. 1998). Discrete LMC tracers which have been studied kinematically include star clusters (Freeman, Illingworth & Oemler 1983; Schommer et al. 1992), planetary nebulae (Meatheringham et al. 1988), HII regions and supergiants (Feitzinger, Schmidt-Kaler & Isserstedt 1977), and carbon stars (Kunkel et al. 1997b; Graff et al. 2000; Alves & Nelson 2000; van der Marel et al. 2002). A common result from all these studies is that the line-of-sight velocity dispersion of the tracers is generally at least a factor ~ 2 smaller than their rotation velocity. This implies that the LMC is kinematically cold, and must therefore to lowest approximation be a disk system.

5.1. General Expressions

To understand the kinematics of an LMC tracer population it is necessary to have a general model for the line-of-sight velocity field that can be fit to the data. All studies thus far have been based on the assumption that the mean streaming (i.e., the rotation) in the disk plane can be approximated to be circular. However, even with this simplifying assumption it is not straightforward to model the kinematics of the LMC, because it is so near to us. Its main body spans more than 20° on the sky and one therefore cannot make the usual approximation that "the sky is flat" over the area of the galaxy. Spherical trigonometry must be used, which yields the general expression (van der Marel et al. 2002):

(5.1)

with

(5.2)

In this equation, v_los is the observed component of the velocity along the line of sight. The quantities (, ) identify the position on the sky: is the angular distance from the center and is the position angle with respect to the center (measured from North over East). The kinematical center is at the center of mass (CM) of the galaxy. The quantities (v_sys, v_t, _t) describe the velocity of the CM in an inertial frame in which the sun is at rest: v_sys is the systemic velocity along the line of sight, v_t is the transverse velocity, and _t is the position angle of the transverse velocity on the sky. The angles (i, ) describe the direction from which the plane of the galaxy is viewed: i is the inclination angle (i = 0 for a face-on disk), and is the position angle of the line of nodes, as illustrated in Figure 6. The line-of-nodes is the intersection of the galaxy plane and the sky plane. The velocity V(R') is the rotation velocity at cylindrical radius R' in the disk plane. D₀ is the distance to the CM, and f is a geometrical factor. The quantity s = ± 1 is the `spin sign' that determines in which of the two possible directions the disk rotates.

Figure 6. Schematic illustration of the observer's view of the LMC disk. The plane of the disk is titled diagonally out of the paper. The inclination i is the angle between the (x, y) plane of the sky, and the (x', y') plane of the galaxy disk. The x'-axis is the line of nodes, defined as the intersection of the (x, y) plane of the sky and the (x', y') plane of the galaxy disk. The angle is the position angle of the line of nodes in the plane of the sky.

The first term in equation (5.1) corresponds to the internal rotation of the LMC. The second term is the part of the line-of-sight velocity of the CM that is seen along the line of sight, and the third term is the part of the transverse velocity of the CM that is seen along the line of sight. For a galaxy that spans a small area on the sky (very small ), the second term is simply v_sys and the third term is zero. However, the LMC does not have a small angular extent and the inclusion of the third term is particularly important. It corresponds to a solid-body rotation component. Given the LMC transverse velocity implied by equation (4.1), it rises to an amplitude of 71 km s^-1 at = 10°, which significantly exceeds the amplitude of the intrinsic rotation contribution (first term of eq. [5.1]) at that radius. The fourth term in equation (5.1) describes the line-of-sight component due to changes in the inclination of the disk with time, as are expected due to precession and nutation of the LMC disk plane as it orbits the Milky Way (Weinberg 2000). This term also corresponds to a solid-body rotation component.

The general expression in equation (5.1) appears complicated, but it is possible to gain some intuitive insight by considering some special cases. Along the line of nodes one has that sin( - ) = 0 and cos( - ) = ± 1, so that

(5.3)

Here it has been defined that 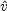_los v_los - v_sys cos v_los - v_sys. The quantity v_tc v_t cos(_t - ) is the component of the transverse velocity vector in the plane of the sky that lies along the line of nodes; similarly, v_ts v_t sin(_t - ) is the component perpendicular to the line of nodes. Perpendicular to the line of nodes one has that cos( - ) = 0 and sin( - ) = ± 1, and therefore

(5.4)

Here it has been defined that w_ts = v_ts + D₀(di / dt). This implies that perpendicular to the line of nodes 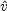_los is linearly proportional to sin. By contrast, along the line of nodes this is true only if V(R') is a linear function of R'. This is not expected to be the case, because galaxies do not generally have solid-body rotation curves; disk galaxies tend to have flat rotation curves, at least outside the very center. This implies that, at least in principle, both the position angle of the line of nodes and the quantity w_ts are uniquely determined by the observed velocity field: is the angle along which the observed 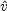_los are best fit by a linear proportionality with sin, and w_ts is the proportionality constant.