4. THE CMB IN COMBINATION WITH OTHER COSMIC PROBES

We learn much more about cosmology when we add to the CMB anisotropy lower redshift observations. The primary CMB anisotropy comes from a surface behind the galaxies and clusters of galaxies which are roughly between us and z 2 (or between now, t_U = 13.7 Gyr, and when the universe was 3.3 Gyr). In regards to cosmic parameters, lower redshift measurements sample the universe in a much different state of it evolution and therefore with different parameter degeneracies. In regards to understanding structure formation, the CMB gives us the initial conditions whereas the lower redshift measurements of the large scale structure (LSS) give us the current condition.

There are a number of ways in which lower z measurements complement the CMB: (a) through measuring the current expansion rate with the Hubble constant; (b) through measuring the current baryon density with quasar absorption systems; (c) through measuring the current mass density with galaxy velocities or the mass-to-light ratio; (d) through measuring the ages of the oldest objects; and (e) through measuring the matter power spectrum with gravitational lensing (e.g., Contaldi, Hoekstra, & Lewis 2003) or galaxy surveys such as 2dFGRS and SDSS (e.g., Gunn et al. 1998). ⁽³⁾

The complementarity of the Hubble constant has been discussed above; and the other probes, of course, have a rich history. Since the last IAU, huge strides were made in determining the matter power spectrum as we discuss below. The supernovae results are not included in the list because it still seems best to treat the CMB+LSS as an independent probe of negative pressure.

The power spectrum from galaxies, P_g(k), and the CMB power spectrum are intimately related. However, technical issues arise when comparing the two because one is not certain how fluctuation in the number density of galaxies trace the fluctuations in matter. In other words, the galaxy population might be biased with respect to the matter density which the CMB probes. The bias is quantified as P_g(k) = b² P(k) where P(k) is the matter power spectrum and b is the bias factor. For example, it is observed that redder (e.g., IRAS) galaxies cluster together less strongly than do optically selected ones and are thus less strongly biased (Fisher et al. 1994). Similarly, luminous galaxies are more biased than less luminous ones (Norberg et al. 2001).

The amplitude of the matter power spectrum is set by ₈, the rms fluctuations in the matter mass density in a comoving sphere of diameter 8 Mpc. In order to determine ₈, one needs to know the cosmic matter density, _m, which is only determined to 30% accuracy (as opposed to the physical matter density which is determined to 15% accuracy). In the CMB, ₈² simply scales the overall amplitude of the angular power spectrum, whereas _m is sensitive to the shape of the spectrum.

Figure 5 shows a comparison of the CMB power spectrum and P(k). The big leap in galaxy surveys in the past few years is that the 2dFGRS survey was able to measure the matter power precisely and over a large range in k, particularly values of k directly probed by the CMB. The two data sets are combined by comparing their shapes and amplitudes as discussed in Verde et al. (2003).

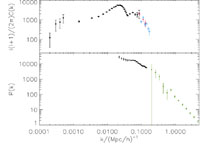Figure 5. Top: the CMB angular power spectrum as a function of comoving wavenumber k ( k l / 14400). The points to the left are from WMAP, the data for l > 875 are from CBI and ACBAR. Bottom: the LSS data from 2dFGRS ( 0.01 < k < 0.15) and the Lyman survey (Croft et al. 2002). The power spectra have been rescaled to z = 0. To compare the LSS data to the CMB on must take into account redshift-space distortions, non-linearities, bias, window functions, etc. This figure from Verde et al. (2003).

The primary observables that 2dF adds are the extended baseline over which the fluctuations are measured and an independent measure of the dark matter power spectrum. (A value of the bias of b = 1.06 ± 0.11 (Verde et al. 2002) was used in the WMAP analysis.) These break a number of parameter degeneracies inherent in just l < 1000 CMB measurements. For example, it is clear that with a longer baseline in k the spectral index, or overall tilt of the spectrum, can be better determined. It is then easier to determine the optical depth, , and the matter density _m. In Table 1, one can see the improvement in what one can say when the 2dF data are added to the CMB data (WMAP+ACBAR+CBI, Spergel et al. 2003).

The high-z/low-z combination leads to other science as well. With the emergence of these precise probes, one can now constrain the neutrino mass at the levels being probed by particle physics experiments. The phenomena is as follows. When they are relativistic, neutrinos free-stream out of the potential wells. Because neutrinos are relativistic at early times and cool with the expansion of the universe, clustering by neutrinos is suppressed on small scales with respect to large scales. As one increases the cosmic mass density of neutrinos, , while holding _m = _cdm + + _b fixed, the net matter fluctuations, P(k), are also suppressed on small scales (high k). At the same time, the length scale of the suppression moves to smaller values (higher k). By comparing the P(k) from 2dF with the WMAP CMB fluctuations, one finds h² < 0.007 (95% cl) or m < 0.7 eV (95% cl) for three degenerate neutrino species. In a sense, we have started addressing questions of classic particle physics with cosmological probes.

There are also direct correlations expected between the CMB anisotropy and galaxy surveys in addition to the relation between power spectra. Crittenden & Turok (1996) pointed out that in a dominated universe, there should be measurable correlations between the CMB anisotropy and the matter as traced by x-ray or radio sources at large angular scales. The mechanism is that the gravitational potential wells change, due to the -induced acceleration, while a CMB photon traverses it. This in turn affects the energy of the photons (ISW effect). These same potential wells are traced by galaxy populations around z ~ 2. The correlation has been seen albeit at only about the 3 level (Boughn & Crittenden 2003, Nolta et al. 2003, Fosalba, Gaztananga & Castander 2003, Scranton et al. 2003).

The standard model has many predictions and consistency checks that are currently being tested. For the CMB, a number of the correlations that should exist are given in Peiris & Spergel (2000). Of course, the pay dirt is in the inconsistencies!

³ The SDSS / WMAP analysis came out after the IAU. Back.