IV. RELATIVISTIC EFFECTS

A. Compactness and relativistic motion

The first theoretical clues to the necessity of relativistic motion in GRBs arose from the Compactness problem [353]. The conceptual argument is simple. GRBs show a non thermal spectrum with a significant high energy tail (see Section IIA1). On the other hand a naive calculation implies that the source is optically thick. The fluctuations on a time scale t imply that the source is smaller than c t. Given an observed flux F, a duration T, and an distance d we can estimate the energy E at the source. 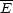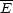For a typical photon's energy this yields a photon density 4 d² F / c³ t². Now, two -rays can annihilate and produce e⁺e^- pairs, if the energy in their CM frame is larger than 2m_e c². The optical depth for pair creation is:

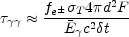(5)

where, f_e^± is a numerical factor denoting the average probability that photon will collide with another photon whose energy is sufficient for pair creation. For typical values and cosmological distances, the resulting optical depth is extremely large _e^± ~ 10¹⁵ [306]. This is, of course, inconsistent with the non-thermal spectrum.

The compactness problem can be resolved if the emitting matter is moving relativistically towards the observer. I denote the Lorentz factor of the motion by . Two corrections appear in this case. First, the observed photons are blue shifted and therefore, their energy at the source frame is lower by a factor . Second, the implied size of a source moving towards us with a Lorentz factor is c t ² (see Section IVB below). The first effect modifies f_e^± by a factor ^-2 where is the photon's index of the observed -rays (namely the number of observed photons per unit energy is proportional to E^-). The second effect modifies the density estimate by a factor ^-4 and it influences the optical depth as ^-2. Together one finds that for ~ 2 one needs 100 to obtain an optically thin source.

The requirement that the source would be optically thin can be used to obtain direct limits from specific bursts on the minimal Lorentz factor within those bursts [15, 91, 199, 220, 306, 308, 442]. A complete calculation requires a detailed integration over angular integrals and over the energy dependent pair production cross section. The minimal Lorentz factor depends also on the maximal photon energy, E_max, the upper energy cutoff of the spectrum. Lithwick and Sari [220] provide a detailed comparison of the different calculations and point our various flaws in some of the previous estimates. They find that:

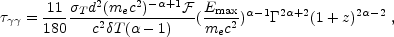(6)

where the high end of the observed photon flux is given by E^- (photons per cm² per sec per unit photon energy). A lower limit on is obtained by equating Eq. 6 to unity.