B. Relativistic time effects

Consider first a source moving relativistically with a constant velocity along a line towards the observer and two photons emitted at R₁ and R₂. The first photon (emitted at R₁) will reach the observer at time (R₂ - R₁) / v - (R₂ - R₁) / c before the second photon (emitted at R₂). For >> 1 this equals (R₂ - R₁) / 2c ². This allows us to associate an "observer time" R / 2c ² with the distance R and for this reason I have associated a scale c t ^-2 with fluctuations on a time scale t in the optical depth equation earlier (see Section IVA). This last relation should be modified if the source moves a varying velocity (v=v(R)). Now

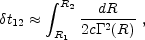(7)

which reduces to

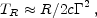(8)

for motion with a constant velocity. The difference between a constant velocity source and a decelerating source introduces a numerical factor of order eight which is important during the afterglow phase [363].

Consider now a relativistically expanding spherical shell, or at least a shell that is locally spherical (on a scale larger than 1 / ). Emission from parts of the shell moving at angle relative to the line of sight to the observer will arrive later with a time delay R(1 - cos) / c. For small angles this time delay equals R² / 2c. As the radiation is beamed with an effective beaming angle 1 / most of the radiation will arrive within a typical angular time scale:

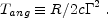(9)

The combination of time delay and blueshift implies that if the emitted spectrum is a power law spectrum with a spectral index then the observed signal from the instantaneous emission of a thin shell will decay at late time as a power law with t^-(2-) [94, 272]. The observed pulse from an instantaneous flash from a thin shell is shown in Fig. 14.

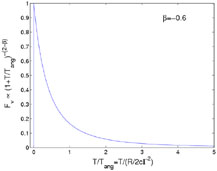Figure 14. The observed pulse from an instantaneous flash from a spherical relativistic thin shell moving relativistically and emitting emitting with a power low -0.6.

As I discuss later (see Section VIA) the similarity between the angular time scale and the radial time scale plays a crucial role in GRB models.