F. Polarization from Relativistically Moving Sources

Polarization can provide information on both the emission process and on the geometry of the emitting regions. Usually the observed polarization is obtained by first integrating the Stokes parameters of the radiation emitted by the individual electrons over the electron's distribution. This yields the local polarization. Then we integrate over the emitting region to obtain the global polarization. In GRBs (both in the prompt emission and in the afterglow) the emitting regions move relativistically towards the observed. The implied Lorentz transformations play a very important role in the second integration as they change the direction of propagation of the photons and hence the direction of the local polarization. The final results are sometimes surprising and counter intuitive. For example even if the intrinsic (local) emission is 100% polarized in the same direction the integration over the emitting region would reduce this to 70% polarization. I consider polarization from synchrotron emission here, but the results can be easily applied to IC as well. I apply the results derived in this section to the possible polarization from the prompt emission and from the afterglow in the corresponding sections Section VIE and VIIJ.

As an example I consider synchrotron emission. Synchrotron emission is polarized with and the intrinsic local polarization level depends on the spectral index of the energy distribution of the emitting electrons, p, [361]. For typical values (2 < p < 3) it can reach 75%. The polarization vector is perpendicular to the magnetic field and, of course, to the direction of the emitted radiation. The formalism can be easily adopted also to Inverse Compton for which the intrinsic local polarization is higher and could reach 100% when the photons are scattered at 90°.

Consider first a case where the magnetic field is uniform locally (over a regions of angular size ^-1). This could happen, for example, if we have an ordered magnetic field along the direction and the observer is more than ^-1 away from the symmetry axis. This would be the case within internal shocks if the magnetic field is dragged from the source or within several Poynting flux dominated models. The locally emitted polarization is uniform and is in the plane of the sky and perpendicular to the direction of the magnetic field. In a Newtonian system it would combine so that the observed polarization equals the emitted one. However, the Lorentz transformations induce their own signature on the observed polarization [133, 134]. This is depicted in Fig. 15. It is clear from this figure that the polarization vector varies along the observed region (whose angular size is 1 / . Consequently the observed global polarization will be smaller than the local polarization.

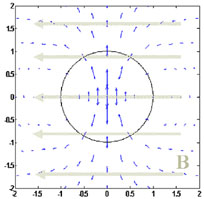Figure 15. Polarization from a uniform magentic field (following [134]). The circle marks the and angle where the matter moves at an angle -1 from the observer. Note that the polarization is maximal along the line perpendicular to the uniform field but it vanished in the other direction near the -1 circle.

The fluxes depend on how the intensity varies with the magnetic field. For I B⁰, which is relevant for fast cooling ⁵ (and the prompt GRB), the time integrated stokes parameters (note that V = 0 as the polarization is linear) and polarization are given by:

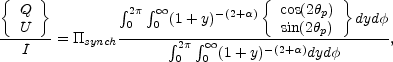(39)

and the relative polarization is given by

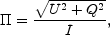(40)

where _p = + arctan((1 - y) / (1 + y) cot) [134] (see also [228]). For = 1 Eqs. 39-40 yield a polarization level of 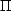/ 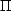_synch 60%. I.e. 60% of the maximal synchrotron polarization, or an overall polarization of ~ 45%. Taking the exact values of and the dependence of I on B for fast cooling and p = 2.5 results in an overall polarization of ~ 50% [134, 275].

It turns out that one can get a polarized emission even from random magnetic field Gruzinov and Waxman [148] and Medvedev and Loeb [255]. This happens if the system has non spherical geometry. Consider a two dimensional random magnetic field which is in the plane of the shock and assume that the correlation length of this magnetic field is very short compared to all other length scales in the system. The Lorentz transformation induce in this case a radial polarization pattern going out from the center (where the velocity of the matter is towards the observer and the polarization vanishes). This polarization pattern is shown in Fig. 16. It is clear that a simple integration over this pattern will lead to a vanishing polarization.

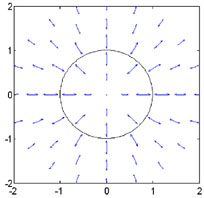Figure 16. Polarization from a random magnetic field in the plane of the shock [275]. The solid circle marks the and angle where the matter moves at an angle -1 from the observer. Polarization can arise if we view a part of a jet (dashed line), or if the emission is dominated by hot spot (dashed - dotted regions) or if there is an overall gradient of the emissivity as would arise in the standard jet model.

However, a net polarization can arise in several cases if the overall symmetry is broken. Polarization will arise if (see Fig. 16):

• We observe a jet in an angle so that only a part of the jet is within an angle of ^-1.

• If the emission is nonuniform and there are stronger patches with angular size smaller than ^-1from which most of the emission arise.

• We observe a standard jet whose emission is angle dependent and this dependence is of the order of ^-1.

Ghisellini and Lazzati [126], Gruzinov [147], Sari [365], Waxman [432] suggested that polarization can arise from a jet even if the magnetic field is random. Nakar et al. [275] considered a random magnetic field that remains planner in the plane of the shock (for a three dimensional random magnetic field the polarization essentially vanishes). For I B⁰ the degree of observed polarization of the emission emitted from a small region at angle y is: (y) / _synch = min(y, 1 / y). The overall time integrated stokes parameters are:

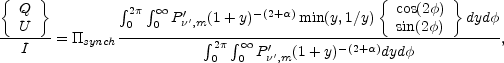(41)

where P'_{', m} = P'_{', m}(y, ) is the emitted power at the synchrotron frequency in the fluid rest frame. For a top-hat jet with sharp edges P'_{', m} is constant for any y and within the jet and zero otherwise. For a structured jet P'_{', m} depends on the angle from the jet axis.

The maximal polarization is observed when one sees the edge of the jet. The probability to see the edge of a top-hat jet with sharp edges and an opening angle _j >> 1 is negligible. On the other hand a jet with _j << 1 is not expected. Thus the only physical cases in which we can expect a large polarization are 1 _j < a few.

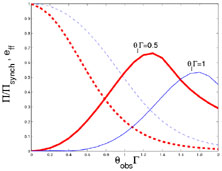
Fig. 17 depicts the time integrated polarization and the efficiency from sharp edged jets with different opening angles as a function of the angle between the jet axis and the line of sight, _obs. The efficiency, e_ff is defined to be the ratio between the observed fluence at _obs and the maximal possible observed fluence at _obs = 0. In all these cases the polarization is peaked above 40%, however the efficiency decrease sharply as the polarization increase. Thus the probability to see high polarization grows when _j decrease. The probability that _obs is such that the polarization is larger than 30% (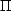^. _synch) while e_ff > 0.1 is 0.68, 0.41, 0.2 & 0.08 for _j = 0.5, 1, 2, 4 respectively. In reality this probability will be smaller, as the chance to observe a burst increases with its observed flux.

Figure 17. The time integrated polarization (solid line) and the efficiency (dashed line) as a function of obs for four different values of j for a random magnetic field.

These later calculations also apply for IC emission [71, 211]. However, in this case the intrinsic local polarization is around 100% and hence one can reach a maximal polarization of ~ 70%.

Polarization could also arise if the magnetic field is uniform over random patches within a region of size ^-1. Here it is difficult, of course to estimate the total polarization without a detailed model of the structure of the jet [148].

⁵ see however Granot [133]. Back.