A. Relativistic Blast Waves and the Blandford-McKee solution

The theory of relativistic blast waves has been worked out in a classical paper by Blandford & McKee (BM) already in 1976. The BM model is a self-similar spherical solution describing an adiabatic ultra relativistic blast wave in the limit >> 1. This solution is the relativistic analogue of the well known Newtonian Sedov-Taylor solution. Blandford and McKee also describe in the same paper a generalization for varying ambient mass density, = ₀(R / R₀)^-k, R being the distance from the center. The latter case would be particularly relevant for k = 2, as expected in the case of wind from a progenitor, prior to the GRB explosion.

The BM solution describes a narrow shell of width ~ R / ², in which the shocked material is concentrated. For simplicity I approximate the solution with a thin homogenous shell. Then the adiabatic energy conservation yields:

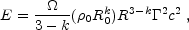(74)

where E is the energy of the blast wave and is the solid angle of the afterglow. For a full sphere = 4, but it can be smaller if the expansion is conical with an opening angle : = 4(1 - cos) 2 ² (assuming a double sided jet). This expression can be simplified using a generalized Sedov scale:

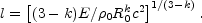(75)

If does not change with time then the blast wave collects ambient rest mass that equals its initial energy at R = l.If we take into account sideway expansion (after the jet break) we find that 1 and the blast wave becomes Newtonian at:

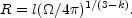(76)

Using the approximate (the numerical factor in this equation assumes that the shell is moving at a constant velocity) time - radius relation Eq. 8 one can invert Eq. 74 (using the definition of l , Eq. 75) and obtain R and as a function of time:

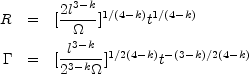(77)

The time in these expressions is the observer time - namely the time that photons emitted at R arrive to the observer (relative to the time that photons emitted at R = 0). For spherical (or spherical like) evolution in these expressions is a constant. In general it is possible that varies with R or with (as is the case in a sideways expansion of a jet). This will produce, of course, a different dependence of R and on t.

The values of R and from Eq. 78 can be plugged now into the typical frequencies _c, _m and _sa as well into the different expression for F_{, max} to obtain the light curve of the afterglow.

Alternatively, one can calculate the light curve using a more detailed integration over the BM density and energy profiles. To perform such integration recall that the radius of the front of the shock is:

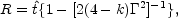(78)

where (t) is the shock's Lorentz factor and 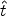is the time since the explosion in its rest frame. The different hydrodynamic parameters behind the shock can be expressed as functions of a dimensionless parameter :

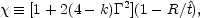(79)

as:

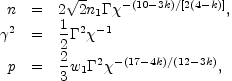(80)

where n₁ and w₁ are the number density and enthalpy density of the undisturbed circumburst material and n and p are measured in the fluid's rest frame.

The BM solution is self-similar and assumes >> 1. Obviously, it breaks down when R ~ l. This Relativistic-Newtonian transition should take place around

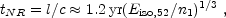(81)

where the scaling is for k = 0, E₅₂ is the isotropic equivalent energy, E_iso = 4 E / , in units of 10⁵² ergs and n₁ is the external density in cm^-3. After this transition the solution will turn into the Newtonian Sedov-Taylor solution with:

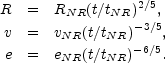(82) (83)

The adiabatic approximation is valid for most of the duration of the afterglow. However, during the first hour or so (or even for the first day, for k = 2), the system could be radiative (provided that _e 1) or partially radiative. During a radiative phase the evolution can be approximated as:

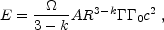(84)

where ₀ is the initial Lorentz factor. Cohen et al. [58] derived an analytic self-similar solution describing this phase.

Cohen and Piran [57] describe a solution for the case when energy is continuously added to the blast wave by the central engine, even during the afterglow phase. A self-similar solution arises if the additional energy deposition behaves like a power law. This would arise naturally in some models, e.g. in the pulsar like model [413].