7. TEMPORAL STRUCTURE AND KINEMATIC CONSIDERATIONS

General kinematic considerations impose constraints on the temporal structure produced when the energy of a relativistic shell is converted to radiation. The enormous variability of the temporal profiles of GRBs from one burst to another in contrast to the relatively regular spectral characteristics, was probably the reason that until recently this aspect of GRBs was largely ignored. However, it turns out that the observed temporal structure sets a strong constraint on the energy conversion models [20, 230]. GRBs are highly variable (see section 2.2) and some configurations cannot produce such temporal profiles.

7.1. Time-scales

Special relativistic effects determine the observed duration of the burst from a relativistic shell (see Fig. 14).

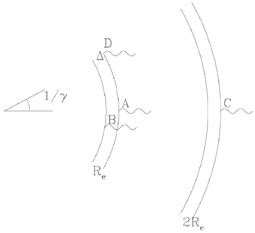Figure 14. Different time scales in terms of the arrival time of four photons: tA,tB, tC, and tD. Tradial = tC - tA; Tangular = tD - tA, / c = tB - tA.

• The Radial Time Scale: T_radial: Consider an infinitely thin relativistic shell with a Lorentz factor _E (the subscript E is for the emitting region). Let R_E be a typical radius characterizing the emitting region (in the observer frame) such that most of the emission takes place between R_E and 2R_E. The observed duration between the first photon (emitted at R_E) and last one (emitted at 2R_E) is [205, 18]:

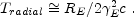  (29)

• The Angular Time Scale: T_ang: Because of relativistic beaming an observer sees up to solid angle of _E^-1 from the line of sight. Two photons emitted at the same time and radius R_E, one on the line of sight and the other at an angle of _E^-1 away travel different distances to the observer. The difference lead to a delay in the arrival time by [205, 18, 230] :

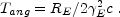  (30)

  Clearly this delay is relevant only if the angular width of the emitting region, is larger than _E^-1.

In addition there are two other time scales that are determined by the flow of the relativistic particles. These are:

• Intrinsic Duration: T: The duration of the flow. This is simply the time in which the source that produces the relativistic flow is active. T = / c, where is the width of the relativistic wind (measured in the observer's rest frame). For an explosive source R_i. However, could be much larger for a wind. The observed duration of the burst must be longer or equal to / c

• Intrinsic Variability T: The time scale on which the inner source varies and produces a subsequent variability with a length scale = cT in the flow. Naturally, T sets a lower limit to the variability time scale observed in any burst.

Clearly and must satisfy:

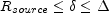(31)

Finally we have to consider the cooling time scale.

• The Cooling Time Scale: T_cool This is the difference in arrival time of photons while the shocked material cools measured in the rest frame of an observer at rest at infinity. It is related to the local cooling time, e / P (where e is the internal energy density and P is the power radiated per unit volume) in the fluid's rest frame by:

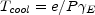  (32)

  Note that this differs from the usual time dilation which gives _Ee / P.

  For synchrotron cooling there is a unique energy dependence of the cooling time scale on frequency: T_cool() ^-1/2 [103] (see Eq. 59). If T_cool determines the variability we will have T() ^-1/2. This is remarkably close to the observed relation: T ^-0.4 [102]. Quite generally T_cool is shorter than the hydrodynamics time scales [103, 232, 69]. However, during the late stages of an afterglow, T_cool becomes the longest time scale in the system.