Gamma-Ray Bursts and the Fireball Model

7.2. Angular Spreading and External shocks

Comparison of Eqs. 29 and 30 (using Delta R_E ltapprox R_E) reveals that T_ang approx T_radial. As long as the shell's angular width is larger than gamma ^-1, any temporal structure that could have arisen due to irregularities in the properties of the shell or in the material that it encounters will be spread on a time given by T_ang. This means that T_ang is the minimal time scale for the observed temporal variability: delta T geq T_ang.

Comparison with the intrinsic time scales yields two cases:

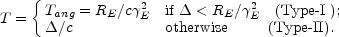(33)

In Type-I models, the duration of the burst is determined by the emission radius and the Lorentz factor. It is independent of Delta . This type of models include the standard "external shock model" [27, 18, 233] in which the relativistic shell is decelerated by the ISM, the relativistic magnetic wind model [226] in which a magnetic Poynting flux runs into the ISM, or the scattering of star light by a relativistic shell [234, 235].

In Type-II models, the duration of the burst is determined by the thickness of the relativistic shell, Delta (that is by the duration that the source is active and produces the relativistic wind). The angular spreading time (which depends on the the radius of emission) is shorter and therefore irrelevant. These models include the "internal shock model" [28, 29, 30], in which different parts of the shell are moving with different Lorentz factor and therefore collide with one another. A magnetic dominated version is given by Thompson [224].

The majority of GRBs have a complex temporal structure (e.g. section 2.2) with ident T / delta T of order 100. Consider a Type-I model. Angular spreading means that at any given moment the observer sees a whole region of angular width gamma _E^-1. Any variability in the emission due to different conditions in different radii on a time scale smaller than T_ang is erased unless the angular size of the emitting region is smaller than gamma _E^-1. Thus, such a source can produce only a smooth single humped burst with = 1 and no temporal structure on a time-scale delta T < T. Put in other words a shell, of a Type-I model, and with an angular width larger than gamma _E^-1 cannot produce a variable burst with >> 1. This is the angular spreading problem.

On the other hand a Type-II model contains a thick shell Delta > R_E / gamma _E² and it can produce a variable burst. The variability time scale, is again limited delta T > T_ang but now it can be shorter than the total duration T. The duration of the burst reflects the time that the "inner engine" operates. The variability reflects the radial inhomogeneity of the shell which was produced by the source (or the cooling time if it is longer than delta / c). The observed temporal variability provides an upper limit to the scale of the radial inhomogeneities in the shell and to the scale in which the "inner engine" varies. This is a remarkable conclusion in view of the fact that the fireball hides the "inner engine".

Can an external shock give rise to a Type-II behavior? This would have been possible if we could set the parameters of the external shock model to satisfy R_E leq 2 gamma _E c delta T. As discussed in 8.7.1 the deceleration radius for a thin shell with an initial Lorentz factor gamma is given by

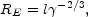(34)

and the observed duration is l gamma ^-8/3 / c. The deceleration is gradual and the Lorentz factor of the emitting region gamma _E is similar to the original Lorentz factor of the shell gamma . It seems that with an arbitrary large Lorentz factor gamma we can get a small enough deceleration radius R_E. However, Eq. 34 is valid only for thin shells satisfying Delta > l gamma ^-8/3 [233]. As gamma increases above a critical value gamma geq gamma _c = (l / Delta )^3/8 the shell can no longer be considered thin. In this situation the reverse shock penetrating the shell becomes ultra-relativistic and the shocked matter moves with Lorentz factor gamma _E = gamma _c < gamma which is independent of the initial Lorentz factor of the shell gamma . The deceleration radius is now given by R_E = Delta ^1/4 l^3/4, and it is independent of the initial Lorentz factor of the shell. The behavior of the deceleration radius R_E and observed duration as function of the shell Lorentz factor gamma is given in Fig. 15 for a shell of thickness Delta = 3 × 10¹²cm. This emission radius R_E is always larger than Delta / gamma _E² - thus an external shock cannot be of type II.

Figure 15. The deceleration radius R_e and the Lorentz factor of the shocked shell gamma _e as functions of the initial Lorentz factor gamma , for a shell of fixed width Delta = 3 × 10¹² cm. For low values of gamma , the shocked material moves with Lorentz factor gamma _e ~ gamma . However as gamma increases the reverse shock becomes relativistic reducing significantly the Lorentz factor gamma _e < gamma . This phenomena prevents the "external shock model" from being Type-II.