9.2. Phases in a Relativistic Decelerating Shell

There are several phases in the deceleration of a relativistic shell: fast cooling (with either radiative or adiabatic hydrodynamics) is followed by slow cooling (with adiabatic hydrodynamics). Then if the shell is non spherical its evolution changes and a phase of sideways expansion and much faster slow down begins when the Lorentz factor reaches ^-1 [258]. Finally the shell becomes Newtonian when enough mass is collected and 1. In the following we estimate the time scale for the different transitions. We define _e,min c _e(m_p / m_e) and t_obs = (1 + z) R / 4 c_t c ² such that the factors c and c_t reflect some of the uncertainties in the model. The canonical values of these factors are: c 0.5 and c_t 1.

The deceleration begins in a fast cooling phase. If _e is close to unity than this cooling phase will also be radiative. The first transition is from fast to slow cooling. There are several different ways to estimate this transition. One can compare the cooling time scale to the hydrodynamic time scale; alternatively one can calculate the fast cooling rate (given by the rate of energy generation by the shell) and compare it to the slow cooling rate (given by the emissivity of the relativistic electrons). We have chosen here to calculate this time as the time when the "typical electron" cools - that is when _c = _m:

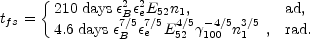(126)

All methods of estimating t_fs give the same dependence on the parameters. However, the numerical factor is quite sensitive to the definition of this transition.

If the solution is initially radiative the transition from fast to slow cooling and from a radiative hydrodynamics to adiabatic hydrodynamics takes place at:

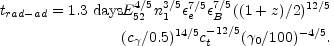(127)

During a radiative evolution the energy in the shock decreases with time. The energy that appears in Eqs. 122 in the radiative scalings is the initial energy. When a radiative shock switches to adiabatic evolution, it is necessary to use the reduced energy to calculate the subsequent adiabatic evolution. The energy E_{f, 52} which one should use in the adiabatic regime is related to the initial E_{i, 52} of the fireball by

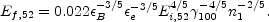(128)

If the shell is not spherical and it has an opening angle: , then the evolution will change when ~ ^-1 [258]. Earlier on the jet expands too rapidly to expand sideways and it evolves as if it is a part of a spherical shell. After this stage the jet expands sideways and it accumulates much more mass and slows down much faster. This transition will take place, quite generally, during the adiabatic phase at:

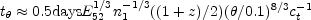(129)

The shell eventually becomes non relativistic. This happens at: R l = (4E₀ / 4 n₁ m_p c²)^1/3 for an adiabatic solution. This corresponds to a transition at:

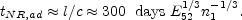(130)

A radiative shell loses energy faster and it becomes non relativistic at R = L = l / ₀^1/3 = (4 E₀ / 4 n_ism m_p c² ₀)^1/3. This will take place at:

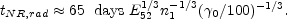(131)

However, the earlier estimate of the transition from fast to slow cooling suggests that the shell cannot remain radiative for such a long time.