


[Refsdal (1964)] first proposed measuring the Hubble constant using gravitationally lensed supernovae 15 years before the discovery of the first gravitationally lensed quasar. In the past two years the status of Hubble constant measurements from time delays has been reviewed by [Courbin (2003)] and by [Kochanek & Schechter (2004)]. Figure 1, taken from Courbin's review, summarizes his report. It should be noted that Courbin deliberately incorporated results representing diverse approaches to computing H0. The average is one standard deviation smaller than the Cepheid result with a comparable uncertainty. It is also in agreement with the CMB results of table 1.
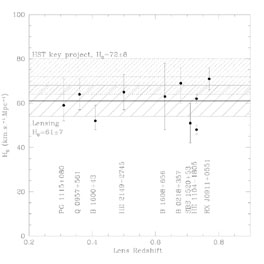 |
Figure 1. Time delay measurements of the Hubble constant, circa 2003 [Courbin (2003)]. |
But if we were to make such a figure today, we might find it less reassuring. The H0 value for PG1115+080 in figure 1 is based on a model for the lensing galaxy that is far from the fundamental plane for ellipticals. The value for RXJ0911+0554 is based on a faulty model [Schechter (2000)] that the present author repudiates in Section 4.4. And the values for HE1104-1805 are based on a time delay that [Ofek & Maoz (2003)] have shown to be too large by a factor of two, driving the points off the top of the plot. The uncertainty in the Hubble constant, as derived from the scatter among systems, would be considerably larger today than it is in figure 1.
In what follows we discuss a number of major difficulties associated with using time delay measurements to measure H0. All but one of the systems in figure 1 are subject to one or more of these difficulties. Before delving into the details, we review the physics upon which the estimate of the Hubble constant is based. 2
2 An excellent, although slightly outdated pedagogical treatment of gravitational lensing can be found in [Narayan & Bartelmann (1999)]. Back.