2.3. The SBBN-predicted Abundances

The primordial abundances of D, ³He, and ⁷Li(⁷Be) are rate limited, depending sensitively on the competition between the nuclear reaction rates (proportional to the nucleon density) and the universal expansion rate. As a result, these nuclides are all potential baryometers. As the Universe expands, the nucleon density decreases so it is useful to compare it to that of the CBR photons: n_N / n. Since this ratio turns out to be very small, it is convenient to introduce

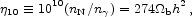(6)

where _b is the ratio of the present values of the baryon and critical densities and h is the present value of the Hubble parameter in units of 100 km s^-1 Mpc^-1 . As the Universe evolves (post-e^± annihilation) this ratio is accurately preserved so that at the time of BBN should be equal to its value today. Testing this relation over ten orders of magnitude in redshift, over a timespan of some 10 billion years, can provide a confirmation of, or pose a challenge to the standard model.

In contrast to the other light nuclides, the primordial abundance of ⁴He (mass fraction Y) is relatively insensitive to the baryon density, but since virtually all neutrons available at BBN are incorporated in ⁴He, Y does depend on the competition between the weak interaction rates (largely fixed by the accurately measured neutron lifetime) and the universal expansion rate. The higher the nucleon density, the earlier can the D bottleneck be breached. Since at early times there are more neutrons (as a fraction of the nucleons), more ⁴He will be synthesized. This latter effect is responsible for a very slow (logarithmic) increase in Y with . Given the standard model relation between time and temperature and the measured nuclear and weak cross sections and decay rates, the evolution of the light-nuclide abundances may be calculated and the relic, primordial abundances predicted as a function of the one free parameter, the nucleon density or . These predictions for SBBN are shown in Figure 1.

Figure 1. The SBBN-predicted primordial abundances of D, 3He, and 7Li (by number with respect to hydrogen), and the 4He mass fraction Y as a function of the nucleon abundance 10. The widths of the bands reflect the theoretical uncertainties.

Not shown on Figure 1 are the relic abundances of ⁶Li, ⁹Be, ¹⁰B, and ¹¹B; for the same range in , all of them lie offscale, in the range 10^-20 - 10^-13. The results shown here are from the BBN code developed and refined over the years by my colleagues at The Ohio State University (OSU). They are in excellent agreement with the published results of the Chicago group (Burles, Nollett, & Turner 2001). Notice that the abundances appear in Figure 1 as bands. These reflect the theoretical uncertainties in the predicted abundances. For the OSU code the errors in D/H and ³He/H are at the ~ 8% level, while they are much larger, ~ 12%, for ⁷Li. Burles et al. (2001), in a reanalysis of the relevant published cross sections, have reduced the theoretical errors by roughly a factor of 3 for D and ³He and a factor of 2 for ⁷Li. The reader may not notice the band shown for ⁴He, since the uncertainty in Y, dominated by the very small uncertainty in the neutron lifetime, is at only the ~ 0.2% level (_Y 0.0005).

Based on the discussion above it is easy to understand the trends shown in Figure 1. D and ³He are burned to ⁴He. The higher the nucleon density, the faster this occurs, leaving behind fewer nuclei of D or ³He. The very slight increase of Y with is largely due to BBN starting earlier at higher nucleon density (more complete burning of D, ³H, and ³He to ⁴He) and higher neutron-to-proton ratio (more neutrons, more ⁴He). The behavior of ⁷Li is more interesting. At relatively low values of ₁₀ 3, mass-7 is largely synthesized as ⁷Li [by ³H(, ) ⁷Li reactions], which is easily destroyed in collisions with protons. So, as increases at low values, destruction is faster and ⁷Li/H decreases. In contrast, at relatively high values of ₁₀ 3, mass-7 is largely synthesized as ⁷Be [via ³He(, )⁷Be reactions], which is more tightly bound than ⁷Li and, therefore, harder to destroy. As increases at high values, the abundance of ⁷Be increases. Later in the evolution of the Universe, when it is cooler and neutral atoms begin to form, ⁷Be will capture an electron and -decay to ⁷Li.