Having reviewed the basic physics and cosmological evolution
underlying BBN and summarized the observational data leading
to a set of adopted primordial abundances, the predictions may
now be confronted with the data. There are several possible
approaches that might be adopted. The following option is
chosen here. First, concentrating on the predictions of SBBN,
deuterium will be used as the baryometer of choice to fix the
baryon-to-photon ratio
. This value
and its uncertainty are then used to "predict" the 3He,
4He, and 7Li abundances,
which are compared to those adopted above. This comparison can
provide a test of the consistency of SBBN as well as identify
those points of "tension" between theory and observation.
This confrontation is carried further to consider the two
extensions beyond the standard model [S
1
(
N
0);
e
0].
4.1. Testing the Standard Model
For SBBN, the baryon density corresponding to the D abundance
adopted here (yD = 2.6 ± 0.4) is
10 =
6.1+0.7-0.5, corresponding to
b =
0.022+0.003-0.002.
This is in outstanding agreement with the estimate of
Spergel et al. (2003),
based largely on the new CBR (WMAP) data
(Bennett et al. 2003):
b
= 0.0224 ± 0.0009. For the baryon density
determined by D, the SBBN-predicted abundance of 3He is
y3 = 1.0 ± 0.1, which is to be compared to the
outer-Galaxy abundance of
y3 = 1.1 ± 0.1, which is suggested by
Bania et al. (2002)
to be nearly primordial. Again, the agreement is excellent.
The tension between the data and SBBN arises with 4He. Given
the very slow variation of YP with
, along with
the very high accuracy of the SBBN-predicted abundance, the primordial
abundance is tightly constrained: YSBBN = 0.248 ± 0.001.
This should be compared with our adopted estimate of Y = 0.238 ±
0.005
(Olive et al. 2000).
Agreement is only at the ~ 5%
level. This tension is shown in Figure 10. This
apparent challenge to SBBN is also an opportunity. As already noted, while
the 4He abundance is insensitive to the baryon density, it is
very sensitive to new physics (i.e. nonstandard universal expansion
rate and/or neutrino degeneracy).
 |
Figure 10. The SBBN-predicted relation between the primordial abundances of D and 4He (mass fraction) is shown by the band, whose thickness represents the uncertainties in the predicted abundances. Also shown by the point and error bars are the adopted primordial abundances of D and 4He (see the text). |
There is tension, too, when comparing the SBBN-predicted abundance of
7Li with the (very uncertain) primordial abundance inferred
from the data. For SBBN the expected abundance is [Li]P =
2.65+0.09-0.11. This is to be compared with the
various estimates above that suggested [Li]P
2.2
± 0.1. In Figure 11 is shown the analog of
Figure 10 for lithium
and deuterium. Depending on the assessment of the uncertainty in the
primordial abundance inferred from the observational data, the conflict
with SBBN may or may not be serious. In contrast to 4He,
7Li is more
similar to D (and to 3He) in that its BBN-predicted abundance is
relatively insensitive to new physics. As a result, this tension, if
it persists, could be a signal of interesting new astrophysics (e.g.,
have the halo stars depleted or diluted their surface lithium?).
 |
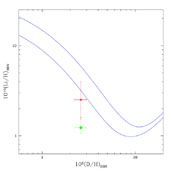Figure 11. The SBBN-predicted relation between the primordial abundances of D and 7Li is shown by the band, whose thickness reflects the uncertainties in the predicted abundances. The data points are for the primordial abundance of D adopted here along with the Ryan et al. (2000) Li abundance (filled circle) and the Pinsonneault et al. (2002) Li abundance (filled triangle). |