4.4. Helium-4 - The BBN Chronometer

The good news about ⁴He is that, as the second most abundant nuclide, it may be observed throughout the Universe. The bad news is that its abundance has evolved since the end of BBN. In order to infer its primordial value it is therefore necessary to track the ⁴He abundance determinations (mass fraction Y_P) as a function of metallicity or, to limit observations to very low metallicity objects. Although, as for D, there are observations of ⁴He in the ISM and the solar system, the key data for determining its primordial abundance comes from observations of metal-poor, extragalactic HII regions. A compilation of current data (courtesy of K. A. Olive) is shown in Figure 5 where the ⁴He mass fraction is plotted as a function of the oxygen abundance; note that the solar oxygen abundance, O/H 5 × 10^-4 (Allende-Prieto, Lambert & Asplund 2001) is off-scale in this figure. These are truly low metallicity HII regions.

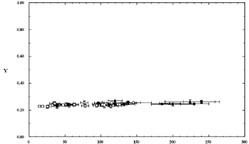Figure 5. The 4He mass fraction Y derived from observations of extragalactic HII regions of low metallicity versus the corresponding HII region oxygen abundances (from K. A. Olive).

It is clear from Figure 5 that the data exist to permit the derivation of a reasonably accurate estimate (statistically) of the primordial ⁴He mass fraction Y_P, with or without any extrapolation to zero-metallicity. What is not easily seen in Figure 5 given the Y_P scale, is that Y_P derived from the data assembled from the literature by [Olive & Steigman (1995)] and [Olive, Skillman & Steigman (1997)] (Y_P = 0.234 ± 0.003) is marginally inconsistent (at ~ 2) with the value derived by [Izotov, Thuan & Lipovetsky (1997)] and [Izotov & Thuan (1998)] from their nearly independent data set (Y_P = 0.244 ± 0.002). In addition, there are a variety of systematic corrections which might modify both data sets (Steigman, Viegas & Gruenwald 1997 ; Viegas, Gruenwald & Steigman 2000; Olive & Skillman 2001; Sauer & Jedamzik 2002; Gruenwald, Steigman & Viegas 2002; Peimbert, Peimbert & Luridiana 2002)

Unless/until the differences in Y_P derived by different authors from somewhat different data sets is resolved and the known systematic errors are corrected for (the unknown ones will always hang over us like the sword of Damocles), the following compromise, adopted by [Olive, Steigman & Walker (2000)], may not be unreasonable. From [Olive & Steigman (1995)] and [Olive, Skillman & Steigman (1997)], the 2 range for Y_P is 0.228 - 0.240, while from the [Izotov, Thuan & Lipovetsky (1997)] and [Izotov & Thuan (1998)] data the 2 range is Y_P = 0.240 - 0.248. Thus, although the current estimates are likely dominated by systematic errors, they span a ~ 2 range from Y_P = 0.228 to Y_P = 0.248. Therefore, as proposed by [Olive, Steigman & Walker (2000)], we adopt here a central value for Y_P = 0.238 and a ~ 1 uncertainty of 0.005: Y_P = 0.238 ± 0.005. Given the approximation (see Section 3) Y 0.16 (S - 1), for _YP 0.005 the uncertainty in S is 0.03 (corresponding to an uncertainty in N of 0.4).