


1.1. Redshift
Light emitted from a comoving galaxy located at
 g at time
te will reach an observer situated at
g at time
te will reach an observer situated at
 o
o
 0 at
a later time to, where
0 at
a later time to, where
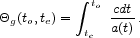 |
(5) |
Equation 5 provides the relation among
 g,
to,
and te. For a comoving galaxy,
g,
to,
and te. For a comoving galaxy,
 g is
unchanged so that differentiating eq. 5 leads to
g is
unchanged so that differentiating eq. 5 leads to
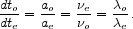 |
(6) |
This result relates the evolution of the universe (ao
/ ae) as
the photon travels from emission to observation, to the change in its
frequency ( ) or wavelength
(
) or wavelength
( ). As the universe
expands
(or contracts!), wavelengths expand (contract) and frequencies decrease
(increase). The redshift of a spectral line is defined by relating
the wavelength at emission (the "lab" or "rest-frame" wavelength
). As the universe
expands
(or contracts!), wavelengths expand (contract) and frequencies decrease
(increase). The redshift of a spectral line is defined by relating
the wavelength at emission (the "lab" or "rest-frame" wavelength
 e) to the
wavelength observed at a later time to,
e) to the
wavelength observed at a later time to,
 o.
o.
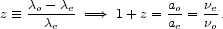 |
(7) |
Since the energies of photons are directly proportional to their
frequencies, as the universe expands photon energies redshift to
smaller values:
E = h
= h 
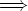 E
E
 (1 +
z)-1. For all particles, massless or not,
de Broglie told us that wavelength and momentum are inversely related,
so that: p
(1 +
z)-1. For all particles, massless or not,
de Broglie told us that wavelength and momentum are inversely related,
so that: p 
 -1
-1
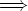 p
p
 (1 +
z)-1. All momenta redshift; for non-relativistic
particles (e.g. galaxies) this implies that their "peculiar"
velocities redshift: v = p/M
(1 +
z)-1. All momenta redshift; for non-relativistic
particles (e.g. galaxies) this implies that their "peculiar"
velocities redshift: v = p/M
 (1 +
z)-1.
(1 +
z)-1.