1.3. Distribution of arrival directions

The distribution of arrival directions is perhaps the most helpful observable in yielding clues about the CR origin. On the one hand, if cosmic rays cluster within a small angular region (see e.g. [46]) or show directional alignment with powerful compact objects (see e.g. [47]), one might be able to associate them with isolated sources in the sky. On the other hand, if the distribution of arrival directions exhibits a large-scale anisotropy, this could indicate whether or not certain classes of sources are associated with large-scale structures (such as the Galactic plane or the Galactic halo).

Cosmic ray air shower detectors which experience stable operation over a period of a year or more can have a uniform exposure in right ascension, . A traditional technique to search for large-scale anisotropies is then to fit the right ascension distribution of events to a sine wave with period 2 / m (m^th harmonic) to determine the components (x, y) of the Rayleigh vector [48]

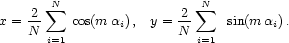(3)

The m^th harmonic amplitude of N measurements of _i is given by the Rayleigh vector length = (x² + y²)^1/2. The expected length of such vector for values randomly sampled from a uniform phase distribution is ₀ = 2 / N. The chance probability of obtaining an amplitude with length larger than that measured is p( ) = e^-k₀, where k₀ = ² / ₀². To give a specific example, a vector of length k₀ 6.6 would be required to claim an observation whose probability of arising from random fluctuation was 0.0013 (a "3" result) [6].

AGASA has revealed a correlation of the arrival direction of the cosmic rays to the Galactic Plane (GP) at the 4 level [49]. The energy bin width which gives the maximum k₀-value corresponds to the region 10^17.9 eV - 10^18.3 eV where k₀ = 11.1, yielding a chance probability of p( _{E ~ EeV}^AGASA) 1.5 × 10^-5. The GP excess, which is roughly 4% of the diffuse flux, is mostly concentrated in the direction of the Cygnus region, with a second spot towards the Galactic Center (GC) [50]. Evidence at the 3.2 level for GP enhancement in a similar energy range has also been reported by the HiRes Collaboration [51]. The existence of a point-like excess in the direction of the GC has been confirmed via independent analysis [52] of data collected with SUGAR. This is a remarkable level of agreement among experiment using a variety of techniques.

At lower energies (~ PeV), the Rayleigh analysis shows no evidence of anisotropy [53]. Hence, the excess from the GP is very suggestive of neutrons as candidate primaries, because the directional signal requires relatively-stable neutral primaries, and time-dilated neutrons can reach the Earth from typical Galactic distances when the neutron energy exceeds 10¹⁸ eV. Arguably, if the Galactic messengers are neutrons, then those with energies below 10¹⁸ eV will decay in flight, providing a flux of cosmic antineutrinos above 1 TeV that should be observable at kilometer-scale neutrino telescopes [54]. A measurement of the -flux will supply a strong confirmation of the GP neutron hypothesis.

For the ultra high energy ( 10^19.6 eV) regime, all experiments to date have reported k₀ << 6.6, 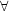m < 5 [55, 56, 57, 58]. ⁽¹⁾ This does not imply an isotropic distribution, but it merely means that available data are too sparse to claim a statistically significant measurement of anisotropy. In other words, there may exist anisotropies at a level too low to discern given existing statistics [59].

The right harmonic analyses are completely blind to intensity variations which depend only on declination, . Combining anisotropy searches in over a range of declinations could dilute the results, since significant but out of phase Rayleigh vectors from different declination bands can cancel each other out. Moreover, the analysis methods that consider distributions in one celestial coordinate, while integrating away the second, have proved to be potentially misleading [60]. An unambiguous interpretation of anisotropy data requires two ingredients: exposure to the full celestial sphere and analysis in terms of both celestial coordinates. In this direction, a recent study [61] of the angular power spectrum of the distribution of arrival directions of CRs with energy > 10^19.6 eV, as seen by the AGASA and SUGAR experiments, shows no departures from either homogeneity or isotropy on angular scale greater than 10°. Finally, the recently analyzed HiRes data is also statistically consistent with an isotropic distribution [62].

All in all, the simplest interpretation of the existing data is that, beyond the ankle, a new population of extragalactic CRs emerges to dominate the more steeply falling Galactic population. Moreover, there are two extreme explanations for the near observed isotropy beyond 10^19.6 eV: one is to argue a cosmological origin for these events, and the other is that we have nearby sources (say, within the Local Supercluster) with a tangled magnetic field in the Galaxy, and beyond, which bends the particle orbits camouflaging the exact location of the sources.

Although there seems to be a remarkable agreement among experiment on predictions about isotropy on large scale structure, this is certainly not the case when considering the two-point correlation function on a small angular scale. The analyses carried out by AGASA Collaboration seem to indicate that the pairing of events on the celestial sky could be occurring at higher than chance coincidence [46, 63]. Specifically, when showers with separation angle less than the angular resolution _min = 2.5° are paired up, AGASA finds five doublets and one triplet among the 58 events reported with mean energy above 10^19.6 eV. The probability of observing these clusters by chance coincidence under an isotropic distribution was quoted as smaller than 1%. A third independent analysis [64], using the Goldberg-Weiler formalism [65], confirmed the result reported by AGASA Collaboration and further showed that the chance probability is extremely sensitive to the angular binning. The "world" data set has also been studied [66]. Six doublets and two triplets out of 92 events with energies > 10^19.6 eV were found, with the chance probability being less than 1% in the restricted region within ± 10° of the super-Galactic plane. The angular two-point correlation function of a combined data sample of AGASA (E > 4.8 × 10¹⁹ eV) and Yakutsk (E > 2.4 × 10¹⁹ eV) was analyzed [67]. For a uniform distribution of sources, the probability of chance clustering is reported to be as small as 4 × 10^-6. Far from confirming what seemed a fascinating discovery, the recent analysis reported by the HiRes Collaboration showed that the data is consistent with no small-scale anisotropy among the highest energy events [68].

The discovery of such clusters would be a tremendous breakthrough for the field, but the case for them is not yet proven. To calculate a meaningful statistical significance in such an analysis, it is important to define the search procedure a priori in order to ensure it is not inadvertently devised especially to suite the particular data set after having studied it. In the analyses carried out by AGASA Collaboration [46, 63], for instance, the angular bin size was not defined ahead of time. Very recently, with the aim to avoid accidental bias on the number of trials performed in selecting the angular bin, the original claim of AGASA Collaboration [46] was re-examined considering only the events observed after the claim [69]. This study showed that the evidence for clustering in the AGASA data set is weaker than was previously claimed, and consistent with the null hypothesis of isotropically distributed arrival directions.

Summing up, the clustering on small angular scale at the upper end of the spectrum remains an open question, and the increase in statistics and improved resolution attainable with PAO is awaited to solve the issue.

¹ For the Fly's Eye data-sample the Rayleigh vector was computed using weighted showers, because it has had a nonuniform exposure in sideral time. A shower's weight depends on the hour of its sideral arrival time, and the 24 different weights are such that every time bin has the same weighted number of showers. Back.