1.4. Propagation of UHECRs

In this section we briefly summarize the relevant interactions that CRs suffer on their trip to Earth. For a more detailed discussion the reader is refer to [1, 70, 71, 72, 73].

1.4.1. The GZK-cutoff

Ever since the discovery of the cosmic microwave background (CMB) standard physics implies there would be a cuttoff in the observed CR-spectrum. In the mid-60's Greisen, Zatsepin, and Kuzmin (GZK) [74, 75] pointed out that this photonic molasses makes the universe opaque to protons of sufficiently high energy, i.e., protons with energies beyond the photopion production threshold,

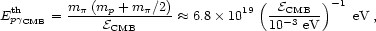(4)

where m_p (m) denotes the proton (pion) mass and _CMB ~ 10^-3 eV is a typical CMB photon energy. After pion production, the proton (or perhaps, instead, a neutron) emerges with at least 50% of the incoming energy. This implies that the nucleon energy changes by an e-folding after a propagation distance (_p n y)^-1 ~ 15 Mpc. Here, n 410 cm^-3 is the number density of the CMB photons, _p > 0.1 mb is the photopion production cross section, and y is the average energy fraction (in the laboratory system) lost by a nucleon per interaction. Energy losses due to pair production become relevant below ~ 10¹⁹ eV. For heavy nuclei, the giant dipole resonance can be excited at similar total energies and hence, for example, iron nuclei do not survive fragmentation over comparable distances. Additionally, the survival probability for extremely high energy ( 10²⁰ eV) -rays (propagating on magnetic fields >> 10^-11 G) to a distance d, p( > d ) exp[- d / 6.6 Mpc], becomes less than 10^-4 after traversing a distance of 50 Mpc.

In recent years, several studies on the propagation of CRs (including both analytical analyses and numerical simulations) have been carried out [76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97]. A summary of the UHECR attenuation lengths for the above mentioned processes (as derived in these analyses) is given in Fig. 2. It is easily seen that our horizon shrinks dramatically for energies 10²⁰ eV. Therefore, if UHECRs originate at cosmological distances, the net effect of their interactions would yield a pile-up of particles around 4 - 5 × 10¹⁹ eV with the spectrum droping sharply thereafter. As one can infer from Fig. 2, the subtleties of the spectral shape depend on the nature of the primary species, yielding some ambiguity in the precise definition of the "GZK cutoff". In what follows we consider an event to superseed the cutoff if the lower energy limit at the 95% CL exceeds 7 × 10¹⁹ eV. This conforms closely to the strong criteria outlined in Ref. [98].

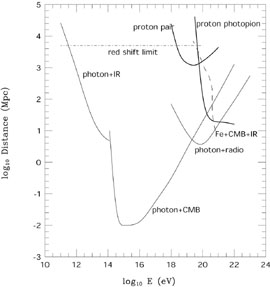Figure 2. Attenuation length of 's, p's, and 56Fe's in various background radiations as a function of energy. The 3 lowest and left-most thin solid curves refer to -rays, showing the attenuation by infra-red, microwave, and radio backgrounds. The upper, right-most thick solid curves refer to propagation of protons in the CMB, showing separately the effect of pair production and photopion production. The dashed-dotted line indicates the adiabatic fractional energy loss at the present cosmological epoch (see e.g. Appendix B of Ref. [1]). The dashed curve illustrates the attenuation of iron nuclei.

1.4.2. Propagation of CRs in a magnetized neighborhood of the Galaxy

In addition to the interactions with the radiation fields permeating the universe, CRs suffer deflections on extragalactic and Galactic magnetic fields.

Over the last few years, it has become evident that the observed near-isotropy of arrival directions can be easily explained if our Local Supercluster contains a large scale magnetic field which provides sufficient bending to the CR trajectories [99, 100]. Intergalactic field strengths and coherent lengths are not well established, but it is plausible to assume that fields have coherent directions on scales 0.5 - 1 Mpc. The Larmor radius of a CR of charge Ze propagating in a magnetic field B_nG B/10^-9 G is given by

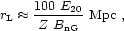(5)

where E₂₀ is the particle's energy in units of 10²⁰ eV. For r_L >> the motion is not very different from quasilinear trajectory, with small deflections away from the straight line path given by

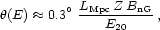(6)

where L_Mpc is the propagation distance in units of Mpc. As the Larmor radius starts approaching the particles begin to diffuse.

Diffusion has two distinctive regimes. Particles that are trapped inside magnetic subdomains (of size _Mpc / Mpc) follow Kolmogorov diffusion. In such a case, the functional dependence of energy of the difussion coefficient is found to be [101]

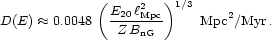(7)

With rising energy, r_L , and there is a transition to Bohm diffusion. The diffusion coefficient in this regime is of order the Larmor radius times velocity (~ c) [102]. In this case the accumulated deflection angle from the direction of the source, can be estimated assuming that the particles make a random walk in the magnetic field [103]

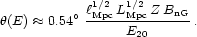(8)

Surprisingly little is actually known about the extragalactic magnetic field strength. There are some measurements of diffuse radio emission from the bridge area between Coma and Abell superclusters that under assumptions of equipartition allows an estimate of 0.2 - 0.6 µG for the magnetic field in this region [104]. ⁽²⁾ Such a strong magnetic field (which is compatible with existing upper limits on Faraday rotation measurements [106]) could be possibly understood if the bridge region lies along a filament or sheet of large scale structures [107]. Faraday rotation measurements [108, 106] have thus far served to set upper bounds of (10^-9 - 10^-8) G on extragalactic magnetic fields on various scales [106, 109], as have the limits on distortion of the CMB [110, 111]. The Faraday rotation measurements sample extragalactic field strengths of any origin out to quasar distances, while the CMB analyses set limits on primordial magnetic fields. Finally, there are some hints suggesting that the extragalactic field strength can be increased in the neighborhood of the Milky Way, B_nG > 10 [112]. Now, using Eq. (5), one can easily see that because of the large uncertainty on the magnetic field strength, (nG) - (µG), all 3 different regimes discussed above are likely to describe UHECR propagation.

If CRs propagate diffusively, the radius of the sphere for potential proton sources becomes significantly reduced. This is because one expects negligible contribution to the flux from times prior to the arrival time of the diffusion front, and so the average time delay in the low energy region, _delay d² / [4D(E)], must be smaller than the age of the source, or else the age of the universe (if no source within the GZK radius is active today, but such sources have been active in the past). Note that the diffuse propagation of UHE protons requires magnetic fields ~ 1µG. Therefore, for typical coherence lengths of extragalactic magnetic fields the time delay of CRs with E 10^18.7 eV cannot exceed _delay 14 Gyr, yielding a radius of d ~ 30 Mpc. In the case CR sources are active today, the radius for potential sources is even smaller d ~ 5 Mpc.

On the other hand, the sphere of potential nucleus-emitting-sources is severely constrained by the GZK cutoff: straightforward calculation, using the attenuation length given in Fig. 2, shows that less than 1% of iron nuclei (or any surviving fragment of their spallations) can survive more than 3 × 10¹⁴ s with an energy 10^20.5 eV. Therefore, the assumption that UHECRs are heavy nuclei implies ordered extragalactic magnetic fields B_nG 15 - 20, or else nuclei would be trapped inside magnetic subdomains suffering catastrophic spallations.

The large scale structure of the Galactic magnetic field carries substantial uncertainties as well, because the position of the solar system does not allow global measurements. The average field strength can be directly determined from pulsar observations of the rotation and dispersion measures average along the line of sight to the pulsar with a weight proportional to the local free electron density, <B_||> 2 µG [113, 114, 115, 116]. (We use the standard, though ambiguous notation, in which B refers to either the Galactic or extragalactic magnetic field, depending on the context.) Measurements of polarized synchrotron radiation as well as Faraday rotation of the radiation emitted from pulsars and extragalactic radio sources revealed that the global structure of the magnetic field in the disk of our Galaxy could be well described by spiral fields with 2 (axisymmetric, ASS) or (bisymmetric, BSS) symmetry [117]. In the direction perpendicular to the Galactic plane the fields are either symmetric (S) or antisymmetric (A). Discrimination between these models is complicated. Field reversals are certainly observed (in the Crux-Scutum arm at 5.5 kpc from the Galactic center, the Carina-Sagittarius arm at 6.5 kpc, the Perseus arm at 10 kpc, and possibly another beyond [118]). However, as discussed by Vallée [119], turbulent dynamo theory can explain field reversals at distances up to ~ 15 kpc within the ASS configuration.

More accurately, the field strength in the Galactic plane (z = 0) for the ASS model is generally described by [120, 121]

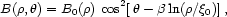(9)

and for the BSS

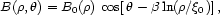(10)

where is the azimuthal coordinate around the Galactic center (clockwise as seen from the north Galactic pole), is the galactocentric radial cylindrical coordinate, and

(11)

Here, ₀ = 10.55 kpc stands for the galactocentric distance of the maximum of the field in our spiral arm, = 1 / tan p (with the pitch angle, p = - 10°), r₀ = 8.5 kpc is the Sun's distance to the Galactic center, and ₁ = 2 kpc. The and coordinates of the field are correspondingly,

(12)

The field strength above and below the Galactic plane (i.e., the dependence on z) has a contribution coming from the disk and another from the halo: (i) for A models

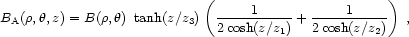(13)

(ii) for S models, B_S = B_A(, , z) / tanh(z / z₃); where z₁ = 0.3 kpc, z₂ = 4 kpc and z₃ = 20 pc. With this in mind, the Galactic magnetic field produce significant bending to the CR orbits if E₂₀ / Z = 0.03 [121].

² Fields of (µG) are also indicated in a more extensive study of 16 low redshift clusters [105]. Back.