2.4. Radio Galaxies and Active Galactic Nuclei

2.4.1. Definitions

Blazars are active galactic nuclei (AGNs) with a) strong flat spectrum radio emission [the power law index > -0.5, with S() ] and/or b) significant optical polarization, and/or c) significant flux variability in the optical and in other wavelengths. When the optical variability occurs on short timescales, the objects are referred to as optically violently variable - OVV - quasars. The blazar classification also includes BL Lacertae (BL Lac) objects, which present a complete or nearly complete lack of emission lines, and highly polarized quasars (HPQs). It also refers, sometimes, to flat spectrum radio quasars (FSRQs), although these are generally more distant, more luminous, and have stronger emission lines. Within the unification model, the underlying scenario for all AGNs is intrinsically similar. At the very center of the galaxy there is a supermassive black hole (~ 10⁶ to ~ 10¹⁰ M) which accretes galactic matter forming an accretion disk. Broad emission lines are produced in clouds orbiting above the disc at high velocity, the broad line region (BLR) and this central region is surrounded by an extended, dusty, molecular torus. A hot electron corona populates the inner region, probably generating continuum X-ray emission. Narrower emission lines are produced in clouds moving much farther from the central black hole. Two-sided jets of relativistic particles emanate perpendicular to the plane of the accretion disc, the generation of which is still not fully understood. Unification of different AGN classes is achieved taken into account the intrinsic anisotropy of the phenomenon, as shown in Fig. 5 (see Refs. [200, 201, 202, 203] for further and more detailed discussions).

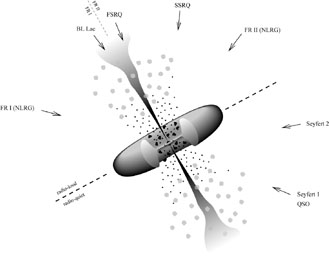Figure 5. The unification model for AGNs. The components of the figure are discussed in the text. Blazars are those AGNs for which the jets are close to line of sight. A regular quasar or a Seyfert 1 galaxy is observed if the orientation angle is ~ 30°, where the narrow-line and broad-line regions are visible. At larger angular offsets, the broad-line region will be hidden by the torus, the corresponding class being Seyfert 2 galaxies. Perpendicular to the jet axis, the full extent of the jets may be seen particular at low frequencies, giving rise to a morphology typical of radio galaxies. The figure is adapted from Refs. [200, 201, 202, 203].

For example, Seyfert galaxies possess a dusty torus of gas at distances intermediate between the BLR and NLR (narrow line region). An observer whose line of sight to the black hole intercepts this torus would see a heavily reddened (or completely extinguished) BLR and central continuum radiation but an unreddened NLR. This would be identified with a Seyfert 2 galaxy. If the line-of-sight does not intercept the torus, the central regions of the nucleus can be observed directly, leading to a Seyfert 1 classification. Radio loud quasars are then objects in which the line-of-sight is close to the jet cone of the source. In the cases in which we are not directly looking into the jet cone -blazars where relativistic effects produce highly variable and continuum dominated emission- emission from the BLR can be observed. Objects with larger inclinations have a less dominant central continuum flux, resulting in Fanaroff-Riley II (FRII) galaxies. If the torus surrounding the black hole obscures the BLR, a narrow line radio galaxy (NLRG) can be observed. It is not clear how FRI radio galaxies fit into such a scheme. Clearly, some (as yet unknown) physical mechanism, probably related to source power, produces different radio morphologies in FRI and FRII sources. ⁽¹⁵⁾ Some blazars may be beamed FRI objects, but there is a lack of broad-line FRI radio galaxies [200]. This make the classification within the unified scheme harder to achieve.

2.4.2. Radiogalaxies

FRII galaxies [205] are the largest known dissipative objects (non-thermal sources) in the Universe. Localized regions of intense synchrotron emission, known as "hot spots", are observed within their lobes. These regions are presumably produced when the bulk kinetic energy of the jets ejected by a central active nucleus (supermassive black hole + accretion disk) is reconverted into relativistic particles and turbulent fields at a "working surface" in the head of the jets [206]. Specifically, the speed v_h with which the head of a jet advances into the intergalactic medium of particle density n_e can be obtained by balancing the momentum flux in the jet against the momentum flux of the surrounding medium. Measured in the frame comoving with the advancing head, v_h v_j [1 + (n_e / n_j)^1/2]^-1, where n_j and v_j are the particle density and the velocity of the jet flow, respectively. v_j > v_h for n_e n_j, and the jet will decelerate. The result is the formation of a strong collisionless shock, which is responsible for particle reacceleration and magnetic field amplification [207]. The acceleration of particles up to ultrarelativistic energies in the hot spots is the result of repeated scattering back and forth across the shock front [208]. Dimensional arguments suggest that the energy density per unit of wave number of MHD turbulence is of the Kolmogorov type [209], and so for strong shocks the acceleration time for protons is [210]

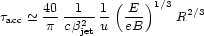(30)

where _jet is the jet velocity in units of c, u is the ratio of turbulent to ambient magnetic energy density in the region of the shock (of radius R), and B is the total magnetic field strength. The acceleration process will be efficient as long as the energy losses by synchrotron radiation and photon-proton interactions do not become dominant. The subtleties surrounding the conversion of a particle kinetic energy into radiation provide ample material for discussion [208, 211, 212, 213, 214, 215]. The proton blazar model relates -ray emission to the development of electromagnetic cascades triggered by secondary photomeson products that cool instantaneously via synchrotron radiation [208, 211, 212, 213, 214]. The synchrotron loss time for protons is given by [216]

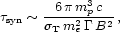(31)

where m_e, m_p, _T and are the electron mass, proton mass, Thomson cross section, and Lorentz factor, respectively. The characteristic single photon energy in synchrotron radiation emitted by an electron is

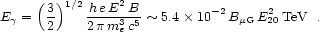(32)

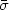
For a proton this number is (m_p / m_e)³ ~ 6 × 10⁹ times smaller. High energy -ray production through proton synchrotron radiation requires very large, (100 G), magnetic fields. Considering an average cross section _p for the three dominant pion-producing interactions [217], p p ⁰, p n ⁺, p p ^{+ -}, the time scale of the energy losses, including synchrotron and photon interaction losses, reads [208]

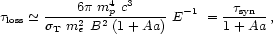(33)

where a stands for the ratio of photon to magnetic energy densities and A gives a measure of the relative strength of p interactions versus the synchrotron emission. Note that the second channel involves the creation of ultrarelativistic neutrons (but _{n p}) with mean free path in the observer rest frame given by _n = _n c _n, where _n ~ 900 s, is the neutron lifetime. Since _n > _p for _{n p max}, such neutrons can readily escape the system, thereby modifying the high end of the proton spectrum. Biermann and Strittmatter [208] have estimated that A 200, almost independently of the source parameters. The most energetic protons injected in the intergalactic medium will have an energy that can be obtained by balancing the energy gains and losses [112]

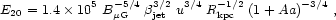(34)

where R_kpc R / 1 kpc.

For typical hot-spot conditions (<B ~ 300 µG, u ~ 0.5, and _jet ~ 0.3) and assuming that the magnetic field of the hot spot is limited to the observable region, one obtains E < 5 × 10²⁰ eV for a < 0.1 [218]. ⁽¹⁶⁾ Particles can also attain ultrahigh energies (E 10²⁰ eV) within the jets or the AGNs themselves. For instance, the knot A in the M87 jet, with a length scale l₈₇ ~ 2 × 10²⁰ cm, has a magnetic field strength B₈₇ ~ 300 µG [219]. Typical AGN sizes are l_AGN ~ 10¹⁵ cm, and B_AGN ~ 1 G [220]. Observational evidence suggests that in the jets a << 1, whereas a ~ 1 for AGNs [208].

2.4.3. Cen A: The source of most UHECRs observed at Earth?

Centaurus A (Cen A) is the nearest active galaxy, ~ 3.4 Mpc [221]. It is a complex FRI radio-loud source identified at optical frequencies with the galaxy NGC 5128. Different multi-wavelength studies have revealed that it comprises a compact core, a jet also visible at X-ray frequencies, a weak counterjet, two inner lobes, a kpc-scale middle lobe, and two giant outer lobes. The jet would be responsible for the formation of the northern inner and middle lobes when interacting with the interstellar and intergalactic media, respectively. There appears to be a compact structure in the northern lobe, at the extrapolated end of the jet. This structure resembles the hot spots such as those existing at the extremities of FRII galaxies. However, at Cen A, it lies at the side of the lobe rather than at the most distant northern edge, and the brightness contrast (hot spot to lobe) is not as extreme [222].

Low resolution polarization measurements in the region of the suspected hot spot give magnetic fields as high as 25 µG [222]. However, in certain regions where measurements at both high and low resolution are available, the B-field amplitude at high resolution can be seen to be twice that at low resolution. The higher resolution can reveal amplification in the post-shock region [223], yielding B-fields possibly as high as 50 - 60 µG [224, 225]. The radio-visible size of the hot spot can be directly measured from the large scale map [226], giving R_HS 2 kpc. The actual size can be larger by a factor ~ 2 because of uncertainties in the angular projection of this region along the line of sight. ⁽¹⁷⁾ Then, if the magnetic field of the hot spot is confined to the visible region, the limiting energy imposed by the Hillas' criterion is E_max ~ 10^20.6 eV.

Estimates of the radio spectral index of synchrotron emission in the hot spot and the observed degree of linear polarization in the same region suggests that the ratio of turbulent to ambient magnetic energy density in the region of the shock is u ~ 0.4 [227]. The jet velocity is model dependent: possible values range from ~ 500 km s^-1 to 0.99 c [222]. For FRI galaxies, the ratio of photon to magnetic energy densities, a, is expected to be << 1. Now, by replacing these numbers into Eq. (34), one can easily see that Cen A can accelerate particles to energies 10²⁰ eV, with a maximum attainable energy set by the Hillas' criterion.

Recent observations of the ray flux for energies > 100 MeV by EGRET [228] allow an estimate L ~ 10⁴¹erg s^-1 for the source. ⁽¹⁸⁾ This value of L is consistent with an earlier observation of photons in the TeV-range during a period of elevated activity [229], and is considerably smaller than the estimated bolometric luminosity L_bol ~ 10⁴³erg s^-1 [221]. Data across the entire ray bandwidth of Cen A is given in Ref. [230], reaching energies as high as 150 TeV [231], though data at this energy await confirmation. For values of B in the µG range, substantial proton synchrotron cooling is suppressed, allowing the production of high energy electrons through photomeson processes. 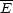The average energy of synchrotron photons scales as 0.29 E [232]. With this in mind, it is straightforward to see that to account for TeV photons, Cen A should harbor a population of ultra-relativistic electrons with E ~ 6 × 10¹⁸ eV. We further note that this would require the presence of protons with energies between one and two orders of magnitude larger, since the electrons are produced as secondaries. ⁽¹⁹⁾

There are plausible physical arguments [214, 233] as well as some observational reasons [234] to believe that when proton acceleration is being limited by energy losses, the CR luminosity L_CR L. Defining , the efficiency of UHECR production compared to high energy production - from the above, 1 - and using equal power per decade over the interval (E_min, E_max), the source luminosity is found to be [235]

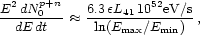(35)

where L₄₁ luminosity of Cen A / 10⁴¹erg s^-1 and the subscript "0" refers to quantities at the source.

For fiducial values, B = 0.5 µG, = 0.5& Mpc, the diffusive distance traveled by CRs with E = 10¹⁹ eV, is c_D = 50 Mpc >> d = 3.4 Mpc. Moreover, one can easily check that for 3.4 Mpc the diffusion time of any proton with energy above the photopion production threshold is always less than the GZK-time, and consequently energy losses can be safely neglected. This implies that the density of protons at the present time t of energy E at a distance r from Cen A (which is assumed to be continuously emitting at a constant spectral rate dN^p+n₀ / dE dt from time t_on until the present) can be obtained by solving the Kolmogorov-diffusive-equation, and is found to be [236]

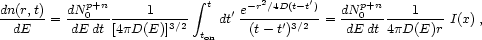(36)

where D(E) is the diffusion coefficient given in Eq. (7), x = 4D T_on / r² T_on / _D, T_on = t - t_on, and

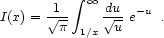(37)

For T_on , the density approaches its time-independent equilibrium value n_eq, while for T_on = _D, n / n_eq = 0.16.

To estimate the power of Cen A, one can evaluate the energy-weighted approximately isotropic proton flux at 1.5 × 10¹⁹ eV, which lies in the center of the flat "low" energy region of the spectrum,

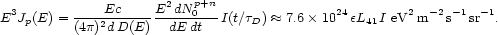(38)

In Eq. (38) we have used the fiducial values of B and as given in the previous paragraph, and set E_min = 1 × 10¹⁹ eV, E_max = 4 × 10²⁰ eV. As noted by Farrar and Piran [235], by stretching the source parameters the "low" energy flux from Cen A could be comparable to that of all other sources in the Universe. To this end, first fix L₄₁ I = 0.40, after comparing Eq. (38) to the observed CR-flux by AGASA: E³ J_obs(E) = 10^24.5 eV² m^-2 s^-1 sr^-1 [63]. Next, L₄₁ 1, determines I 0.40, and consequently the required age of the source T_on to be about 400 Myr, which appears plausible [207, 234]. To maintain flux at the "ankle" for the same T_on, one requires an approximate doubling of L_CR at 5 × 10¹⁸ eV. Because of the larger diffusive time delay at this energy, this translates into an increased luminosity in the early phase of Cen A. From Eq. (32), the associated synchrotron photons are emitted at energies < 30 MeV. The increase in radiation luminosity in this region is not inconsistent with the flattening of the spectrum observed at lower energies [237, 238].

Having identified Cen A to plausibly be a powerful source of UHECRs, we now explore whether B-field deflections provide correct directional properties, i.e., sufficient isotropy. This can be found by computing the incoming current flux density D n as viewed by an observer on Earth, and one finds for a continuously-emitting source a distribution ~ (1 + cos) about the direction of the source, where is the angle to the zenith and

(39)

with x = T_on / _D, and I as defined in Eq. (37) [236]. For our choices of B and , and T_on = 400 Myr, we find for E = 10¹⁹ eV (E = 10²⁰ eV) that = 0.04 ( = 0.07). This is in complete agreement with the upper bounds on dipole anisotropies recently reported by HiRes Collaboration [62]. One caveat is that the large deflection angle of the highest energy Fly's Eye event with respect to the line of sight to Cen A must be explain as a 2 fluctuation [239]. Additionally, Monte Carlo simulations [240] show the predicted auto-correlation function is not consistent with the clustering at small scale reported by AGASA Collaboration [63]. Therefore, if the hypothesis of CR pairing proposed by AGASA Collaboration is confirmed by future data, it will constitute a serious objection to the model outlined above. On the other hand, an interesting observational feature for a Cen A origin of UHECRs is the possible detection of neutrons, which at the highest energies could survive decay and produce a spike in the direction of the source [236]. The estimated event rate at PAO is about 2 direct events per year, against negligible background. Thus, in a few years of running, the hypothesis of Cen A as the source of most UHECRs observed at Earth can be directly tested.

2.4.4. M87: The end of all roads?

M87 is a giant radio galaxy for which there has been a recent report of a TeV excess at a level of 4 [241]. It is also expected to be a source for GLAST, having an EGRET upper limit of 2.8 × 10^-8 photons cm^-2 s^-1 above 100 MeV (Reimer, private communication, see also the limit imposed in Ref. [242]), and comparable theoretical flux predictions [244, 243].

M87 was thought as a high-energy CR emitter since quite long ago [245, 246]. At a distance of 16.3 Mpc [247], it is the dominant radio galaxy in the Virgo cluster (l = 282°, b = 74°) [248]. The emission of synchrotron radiation with a steep cutoff at frequencies about 3 × 10¹⁴ Hz from its radiojets and hot spots [249, 250] implies an initial turbulence injection scale having the Larmor radius of protons at 10²¹ eV.

The major difficulty with a M87 generation of UHECRs is the observation of the nearly isotropic distribution of the CR arrival directions. One can again argue that the orbits are bent. However, the bending cannot add substantially to the travel time, otherwise the energy would be GZK-degraded. An interesting explanation to overcome this difficulty relies on a Galactic wind, akin the solar wind, that would bend all the orbits of the highest energy CRs towards M87 [251, 252]. Indeed, it has long been expected that such a kind of wind is active in our Galaxy [253, 254, 255]. In the analysis of [251], it was assumed that the magnetic field in the Galactic wind has a dominant azimuthal component, with the same sign everywhere. This is because in a spherical wind the polar component of the magnetic field becomes negligible rather quickly, decaying like 1 / r², and thus the azimuthal part of the magnetic field quickly becomes dominant, with B ~ sin / r in polar coordinates [256]. Under these considerations one is left with two degrees of freedom: the strength of the azimuthal component at the location of the Sun, and the distance to which this wind extends. Recent estimates suggest that the magnetic field strength near the Sun is ~ 7 µG [117]. The second parameter is more uncertain. Our Galaxy dominates its near environment well past our neighbor, M31, the Andromeda galaxy, and might well extend its sphere of influence to half way to M81. This implies an outer halo wind of ~ 1.5 Mpc. With this in mind, the mean flight time of the protons in the Galaxy is ~ 5.05 × 10⁶ yr << _s, the time for straight line propagation from M87 (Medina Tanco, private communication). The directions where the 13 highest energy CR events point towards when they leave the halo wind of our Galaxy is consistent with an origin in the Virgo region [251]: (i) for CR protons, except for the two highest energy events, all other events can be traced back to within less than about 20° from Virgo; (ii) if one assumes that the two highest events are helium nuclei, all 13 events point within 20° of Virgo. Arguably, the super-Galactic plane sheet can focus UHECRs along the sheet. Hence, the particles would arrive at the boundary of our Galactic wind with the arrival directions described by an elongated ellipse along the super-Galactic plane sheet [257]. This would allow a bending of 20° to be accomodated.

Additionally, in order to account for most of the CRs observed above the ankle, the power requirement of Virgo cluster [258] needs a fine-tuning of the source direction relative to the symmetry axis of the wind, so as to turn on magnetic lensing effects [259]. In such a case, M87 could be as high as > 10² times more powerful than if unlensed at energies below E / Z ~ 1.3 × 10²⁰ eV. Criticisms of this model [260] have been addressed in [261].

2.4.5. Other powerful nearby radiogalaxies

Apart from Cen A (which would provide the most energetic particles detectable on Earth), the CR-sky above Auger, if populated by radiogaxies, should be dominated by Pictor A (a strong source with a flat radio spectrum) which would contribute with the larger CR flux [218], and PKS 1333-33 [262]. Other two southern candidates would be Fornax A (z = 0.057) and PKS 2152-69 (z = 0.027), which could provide contributions to the CR flux above the cutoff. For other powerful sources and their properties see [218, 263].

There are two additional EGRET sources, one of them at high latitude, for which a possible radio galaxy counterpart has been suggested. One such source is 3EG J1621+8203 (l = 115.5°, b = 31.8°) [264]. 3EG J1621+8203 observations in individual viewing periods yielded near-threshold detections by EGRET, as for Cen A. However, in the cumulative exposure, it was clearly detected and the measured flux above 100 MeV was 1.1 × 10^-7 photon cm^-2 s^-1. The photon spectral index for this source is 2.27± 0.53, steeper than the usual blazar-like spectrum. Mukherjee et al. [264] analyzed the X-ray and radio field coincident with 3EG J1621+8203 and concluded that NGC 6251, a bright FRI radio galaxy [200] at a redshift of 0.0234 (implying a distance 91 Mpc for H₀ = 75 km s^-1 Mpc^-1), and the parent galaxy of a radio jet making an angle of 45° with the line of sight [265], is the most likely counterpart of the EGRET source. With this identification, the implied -ray luminosity is also a factor of 10^-5 below that typical of blazars. Compared with Cen A, the greater distance to NGC 6251 could, perhaps, be compensated by the smaller angle between the jet and the line of sight.

Combi et al. [266] have also recently reported the discovery of a new radio galaxy, J1737-15, within the location error box of the low-latitude -ray source 3EG J1735-1500, whose photon index is = 3.24± 0.47. The radio galaxy morphology at 1.4 GHz is typical of the double-sided FRII. The integrated radio flux is 55.6± 1.5 mJy at 1.4 GHz, the source is non-thermal and it is not detected at 4.8 GHz. Using the relation between approaching and receding jets: S_appr / S_rec = (1 + cos / 1 - cos)^{2 -} , as well as the radio fluxes of each jet component, a viewing angle in the range 79° - 86° for a velocity = v / c between 0.3 and 0.9 and = -1 is derived. Depending on the jet and ambient medium parameters, most double-sided radio sources have sizes below ~ 300 kpc [207]. In the case of J1737-15, and using standard Friedmann-Robertson-Walker models, this size translates into a possible distance smaller than 350 Mpc. If 3EG J1735-1500 is indeed the result of -ray emission in J1737-15, the intrinsic luminosity at E > 100 MeV, at the distance quoted, should then be less than 2 × 10⁴⁴ erg s^-1, also several orders of magnitude smaller than that of blazars. If both radiogalaxies are closer than 100 Mpc, they could also be relevant acceleration sites of the observed UHECRs.

2.4.6. Correlations of UHECRs with QSOs, BL LACs, and EGRET sources

Since an alignment beyond random expectations between UHECRs and QSOs would certainly constitute a great discovery, the possible correlation between UHECRs and QSOs was subject to a great deal of scrutiny. In the spring of 1998, Farrar and Biermann pointed out the existence of a directional correlation between compact radio-QSOs and UHECRs: all events at the high end of the spectrum observed by that time, with energy at least 1 above 10^19.9 eV, were aligned with high redshifted quasars, a phenomenon with a chance probability of occurrence less than 0.5% [47]. Since then, this correlation has been analyzed several times. Hoffman stated that one of the 5 events used in the Farrar and Biermann's study, the highest energy event observed by the Fly's Eye experiment, should not be included in the UHECR sample under analysis, because this very same event was considered to introduce the hypothesis [267]. Without this event, the positive alignment with random background probability is increased to < 3%, in any case small enough as to be plausibly significant [98]. Using an updated event list (twice the size of the previous) from the Haverah Park [33] and the AGASA [63] experiments, Sigl et al. [268] showed that the statistical significance of the alignment is lowered to 27%. Other authors, however, favored the earlier alignment [269], but their correlation signal comes from events with large uncertainty both in energy and in position: they considered events from the SUGAR experiment, although it is not clear whether all these events are above the GZK cutoff. Notwithstanding, after the Haverah Park energy estimates have been re-assessed [129], the original correlation has to be dropped altogether: for the cosmic rays in question, the energy of the 2 events observed by this array with incident zenith angle < 45°, that was previously quoted as > 10^19.9 eV at 1, is now shifted 30% downwards, below the energy cut chosen by Farrar and Biermann. Hence, independently of the statistical test used, when considering only the highest energy (> 10^19.9 eV at 1) events the correlation between UHECRs and QSOs is consistent with a random distribution at the 1 level.

Tinyakov and Tkachev [270, 271, 272] reported a correlation between the arrival directions of UHECRs and BL Lacs. Specifically, the (22) BL Lacs chosen were those identified as such in the (9th-Edition) Veron-Cetty and Veron (2000) [273] catalogue of Quasars and Active Galactic Nuclei, with redshift z > 0.1 or unknown, magnitude m < 18, and radio flux at 6 GHz F₆ > 0.17 Jy. This analysis propose no energy buffer against contamination by mismeasured protons piled up at the GZK energy limit. ⁽²⁰⁾ The evidence supporting their claim is based on 6 events reported by the AGASA Collaboration (all with average energy < 10^19.9 eV), and 2 events recorded with the Yakutsk experiment (both with average energy < 10^19.6 eV), which were found to be within 2.5° of 5 BL Lacs contained in the restricted sample of 22 sources. The chance probability for this coincidence set-up was claim to be 2 × 10^-5. Here also the data set used to make the initial assertion is also being used in the hypothesis testing phase. What is further subject to critique, is that the imposed cuts on the BL Lac catalogue were chosen so as to maximize the signal-to-noise ratio, compensating a posteriori the different cut adjustments by inclusion of a penalty factor [275]. Without such arbitrary cuts, the significance of the correlation signal is reduced at the 1 level. Not to anyone's surprise, even in acceptance of this approach, the estimated value of the penalty factor is subject to debate [275, 272].

Recently, in order to test the hypothetical correlation between UHECRs and BL Lacs, Torres et al. [276] performed a blind analysis using the Haverah Park [277] and Volcano Ranch [278] data samples. Such an analysis shows no positional coincidences between these two samples up to an angular bin > 5°, an angular scale that is well beyond the error in arrival determination of these experiments ( 3°) [66]. On the basis of the strongly correlated sample analyzed by Tinyakov and Tkachev, one expects the distribution describing the correlation between the set of BL Lacs and any UHECR data-set with 33 entries to be Poisson with mean 4.06. This implies a 2 deviation effect. Alternatively, the 95% CL interval of the distribution which samples the correlation between the BL Lacs and CRs recorded by Volcano Ranch + Haverah Park is (0, 3.09) [279], so that the probability to measure the expected mean value 4.06 is << 5%. With this in mind, Torres et al. [276] conclude that the 8 coincidences found in the Tinyakov and Tkachev's analysis do not represent a statistically significant effect.

Additionally, Gorbunov et al. [280] claimed that a set of -ray loud BL Lacs can be selected by intersecting the EGRET, the UHECR, and the BL Lac catalogs (all conveniently cut). The only requirement Gorbunov et al. considered for an object (here, a BL Lac) to be physically associated with an EGRET source is that the angular distance between the best estimated position of the pair does not exceed 2 × R₉₅, where R₉₅ is the 95% confidence level contour of the EGRET detection. Torres et al. [276] pointed out that identifying EGRET sources with BL Lacs (or any other object) just by positional pairing within twice the EGRET error grossly underestimates the goodness of existing -ray data. At this stage, it is worth recalling the reader that the typical R₉₅ radius for EGRET sources is 0.5-1°. One can then argue that if the confidence contours have any significance at all, a source should appear beyond the 95% contour only a few percent of the time. Working with 114 EGRET sources above | b| > 10°, Punsly [281] have estimated the number of random coincidences as a function of the field radius: ~ 2 (10) quasars with more than 1 Jy of 5 GHz flux are expected to correlate by random chance if the size of the typical EGRET angular uncertainty is 0.7° (1.7°), see Fig. 6.

Figure 6. The expected distribution of radio-loud quasars (louder than 0.5 Jy at 5 GHz) to occur by random chance as a function of the distance from the center of the field for a sample of 114 EGRET detections. Points represent the number of -ray detections for which the counterparts are beyond the 95% confidence contour. The dotted curve are the boundaries of the 68% confidence band for the hypothesis that the radio sources are randomly distributed in the EGRET detection fields. Adapted from Punsly (1997). The number of sources whose possible counterpart are beyond the 95% confidence contour is compatible with the chance expectation.

¹⁵ The Faranoff-Riley classification is based on one parameter, R_FR, the ratio of the distance between the regions of highest surface brightness on opposite sides of the central galaxy to the total extent of the source. Objects with R_FR < 0.5 are classified as FRI, whereas those with R_FR > 0.5 are classified as FRII. It is found that the brighter sources are all FRII class, although the distinction between classes is not clear cut in luminosities (for further details see page 220 of Ref. [204]). Back.

¹⁶ The shock structure in hot spots is likely to be much more extended than the visible region in the non-thermal radioemission, as suggested by magnetohydrodynamical modeling [218]. Back.

¹⁷ For example, an explanation of the apparent absence of a counterjet in Cen A via relativistic beaming suggests that the angle of the visible jet axis with respect to the line of sight is at most 36° [222], which could lead to a doubling of the hot spot radius. It should be remarked that for a distance of 3.4 Mpc, the extent of the entire source has a reasonable size even with this small angle. Back.

¹⁸ Note that the received radiation is negligibly affected by interactions with the various radiation backgrounds [215]. Back.

¹⁹ Consecutive factors of ~ 2 energy loss occur in the processes p N ⁰, ⁰ , e⁺ e^-. Eq. (32) then implies proton energies of ~ 10²⁰ eV for 100 TeV photons. Back.

²⁰ The CR sample of Tinyakov and Tkachev consists of 26 events measured by the Yakutsk experiment with energy > 10^19.38 eV [274], and 39 events measured by the AGASA experiment with energy > 10^19.68 eV [63]. Back.