2.3. Neutron stars

2.3.1. Magnetohydronamic acceleration of iron nuclei in pulsars

Following earlier ideas [165] ⁽⁴⁾, Blasi et al. [168] ⁽⁵⁾ have shown that young magnetized neutron stars in our own Galaxy may be one such astrophysical systems.

Neutron stars - endpoints of stellar evolution - begin their life rotating rapidly ( ~ 3000 rad s^-1) and with large surface magnetic fields (B_S 10¹³ G). The dipole component decreases as the cube of the distance from the star's surface B(r) = B_S(R_S / r)³, where the radius of the star is R_S L. At the light cylinder R_lc = c / ~ 10⁷ _3k^-1 cm, where _3k / 3000 rad s^-1, the dipole field cannot be casually maintained, the field is mostly azimuthal, with field lines spiraling outwards [173]. Inside the light cylinder, the magnetosphere corotates with the star, and the density (mostly iron peak elements formed during the supernova event that were stripped off the surface due to strong electric fields) has the Goldreich-Julian value, n_GJ(r) = B(r) / (4 Z e c), where c is the speed of light [174]. The behavior of the plasma outside the light cylinder is still not yet fully understood [175, 176, 177, 178], although some analytical and numerical studies show the development of kinetically dominated relativistic winds (see e.g., [176]).

Blasi et al. [168] assumed that the magnetic field in the wind zone decreases as B(r) B_lcR_lc / r. For surface fields of B_S 10¹³ B₁₃ G, the field at the light cylinder is B_lc = 10¹⁰ B_{13 3k}³. G. The maximum energy of particles that can be contained in the wind near the light cylinder is

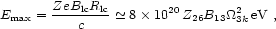(16)

where Z₂₆ Z / 26. The typical energy of the accelerated CRs, E_cr, can be estimated by considering the magnetic energy per ion at the light cylinder E_cr B_lc² / 8 n_GJ. At the light cylinder n_GJ = 1.7 × 10¹¹ B_{13 3k}⁴ / Zcm^-3 which gives

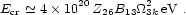(17)

In this model, as the star spins down, the energy of the cosmic ray particles ejected with the wind decreases. The total fluence of UHECRs between energy E and E + dE is

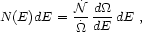(18)

where the particle luminosity is

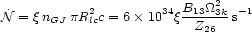(19)

and < 1 is the efficiency for accelerating particles at the light cylinder. For a spin down rate dominated by magnetic dipole radiation, given by I 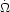= - B_S² R_S^{6 4} / 6c³ where I = 10⁴⁵ g cm² is the moment of inertia, the time derivative of the spin frequency is 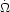= 1.7 × 10^-5 B₁₃² _3k³ s^-1, and Eq. (17) gives

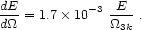(20)

Substituting in Eq. (18), the particle spectrum from each neutron star is

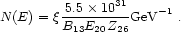(21)

Taking the confining volume for these particles to be V_c and the lifetime for confinement to be t_c, the UHECR density is n(E) = N(E) t_c / V_c, and the flux at the surface of the Earth is F(E) = n(E) c / 4. For a characteristic confinement dimension of R = 10 R₁ kpc, V_c = 4 R³ / 3 and t_c = QR / c, where Q > 1 is a measure of the how well the UHECR are trapped. With this in mind, the predicted UHECR flux at the Earth is [168] ⁶

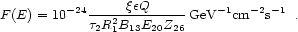(22)

Here, the fact that neutron stars are produced in our Galaxy at a rate 1 / , where 100 ₂ yr, but that not all them (but rather only a fraction ) have the required magnetic fields, initial spin rates and magnetic field geometry to allow efficient conversion of magnetic energy into kinetic energy of the flow, were taken into account. By comparing with observations, the required efficiency factor, , can be estimated, and it only needs to be 4 × 10^-6 Q^-1.

The condition that a young neutron star could produce the UHECRs ⁽⁷⁾ is that E_cr exceeds the needed energy when the envelope becomes transparent (i.e. before the spinning rate of the neutron star decreases to the level where the star is unable to emit particles of the necessary energy), E_cr(t_tr) > 10²⁰ E₂₀ eV. This translates into the following condition [168] ⁽⁸⁾

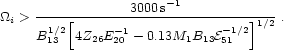(23)

Eq. (23) translates in turn into upper bounds on the surface magnetic field strength and the star initial spin period P_i = 2 / _i,

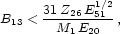(24)

and

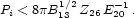(25)

For M₁ = 2 and E₂₀ = E₅₁ = Z₂₆ = 1, Eq (24) gives B₁₃ < 15.4, whereas Eq. (25) leads to P_i 10 ms, not very restrictive values for a young neutron star, see for example the Parkes Multibeam Pulsar Survey. ⁽⁹⁾

2.3.2. Magnetars

Magnetars, neutron stars with surface dipole fields on the order of 10¹⁵ G [183, 184, 185, 186, 187], were also proposed as plausible sites for the generation of UHECRs [188]. Assuming that they occur occur in all galaxies which form massive stars (then avoiding the large-distance GZK problem), and thus that the UHECR are arriving from outside our own Galaxy, the luminous infrared galaxies are preferred sites to search for a magnetar origin of CRs (see [189] and below the discussion in Section 2.7).

The magnetar model for the acceleration of UHECRs proposed by Arons [188] is a variant of that using neutron stars outlined in the previous Section. The theory predicts an injection of charged particles with maximum energy

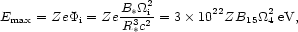(26)

where B_* is a magnetar's surface magnetic field, B₁₅ = B_* / 10¹⁵ Gauss, _i = 10⁴ ₄ s^-1 is the initial angular velocity of the neutron star, R_* is the stellar radius, and c is the speed of light. The initial rotation period is P_i = 0.64 / ₄ ms (if Z = 1 - 2, one requires P_i < 2 - 3 ms for the model to be viable).

The ions actually gain their energy in the relativistic wind electromagnetically expelled from the neutron star at distances r larger than the radii of the star and its magnetosphere. This avoids catastrophic radiation losses; the electric potential in the wind is rE = rB = . As the star spins down, as in the model by Blasi et al., the voltage and the maximum particle energies decline. Summing over the formation and spindown event, one finds a per event injection spectrum proportional to f (E) = E^-1[1 + (E / E_g)]^-1 for E < E_max. Here E_g measures the importance of gravitational wave losses (calculated for a star with static non-axisymmetric quadrupole asymmetry) in spinning the star down. When they exert torques larger than the electromagnetic torque, the star spends less time at the fastest rotation rates (i.e. less time accelerating the highest energy particles), thus causing a steepening in the spectral slope at the highest energies. If the star has an internal magnetic field even stronger than the already large surface field, equatorial ellipticities _e in excess of 10^-3 can exist, in which case E_g would be less than E_max. Three cases of energy loss due to gravitational radiation (GR) were considered in the model: no GR loss (_e = 0, E_g = ); moderate GR loss (_e = 0.01, E_g = 3 × 10²⁰ eV); strong GR loss (_e = 0.1, E_g = 3 × 10¹⁸ eV). If one assumes that all magnetars have exactly the same starting voltage (10^22.5 V), then the model predicts that the spectrum E³J(E) should rise with E above the energy E_g = 2.8 × 10²⁰ eV, where the GZK loss rate becomes approximately energy independent (unless the gravitational wave losses are large) [188]. This prediction will certainly be testable with PAO.

The total number of particles injected per event is

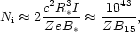(27)

for a stellar radius of 10 km and a moment of inertia I = 10⁴⁵ cgs. The rate at which galaxies inject UHECR into the universe in this model then is 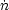_cr = _mag^fast N_i n_galaxy, where n_galaxy 0.02 Mpc^-3 [190], N_i is given by Eq. (27), and _mag^fast is the birth rate of rapidly rotating magnetars per galaxy. Multiplication of the source spectrum q(E) 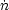_cr f (E) by the energy dependent GZK loss time yields a spectrum received at the Earth in reasonable accord with the existing observations of UHECR if _mag^fast 10^-5 yr^-1 [188]. That fast magnetar birth rate lies between 1% and 10% of the total magnetar birth rate inferred for our galaxy, and about 0.1% of the total core collapse supernova rate in average star forming galaxy, ~ 10^-2 yr^-1 [191].

2.3.3. UHECRs from a pulsar in Cygnus OB2?

As discussed in Sec. 2.1, some evidence may be emerging for a CR accelerator in the Cygnus spiral arm. The HEGRA experiment has detected an extended TeV -ray source in the Cygnus region with no clear counterpart and a spectrum not easily accommodated with leptonic radiation [139]. The difficulty to accommodate the spectrum by conventional electromagnetic mechanisms has been exacerbated by the failure of Chandra and VLA to detect significant levels of X-rays or radiowaves signaling acceleration of any electrons [140]. Especially intriguing is the possible association of this source with part of Cygnus OB2 itself [138], a cluster of several thousands young, hot OB stars with a total mass of ~ 10⁴ M [192]. At a relatively small distance to Earth, 1.7 kpc, this is the largest massive Galactic association. It has a diameter of 60 pc and a core radius of ~ 10 pc. The typical main sequence evolution lifetime of massive O stars is (Myr) and a few tens Myr for massive B stars. Since the O-star population should pass through the Wolf-Rayet phase and explode as supernovae, very fast pulsars are expected to be born in explosions of these massive stars at a rate of about one every ten thousand years.

Apart from the mentioned interpretation of a hadronic production of the TeV radiation within the winds of outlying OB stars of Cyg OB2 [138], it was recently put forward that the TeV emission reported by HEGRA and the CR anisotropy observed at about 10¹⁸ eV in the direction of the Cygnus region can be related to a young pulsar and its pulsar wind nebulae (PWN), born in the Cygnus OB2 association a few ten thousands years ago [193]. The TeV -ray emission would originate in the PWN as a result of interactions of high energy hadrons and/or leptons, whereas there would be a directional CR signal due to neutrons that are dissolved from heavy nuclei accelerated by the pulsar. ⁽¹⁰⁾ Within this model, however, it is hard to explain the absence of counterparts at lower (EGRET) energies at the location of the TeV source, as well as the absence of a stronger X-ray source. ⁽¹¹⁾ However, disregarding these difficulties, an interesting consequence for CR physics can be inferred.

As already discussed in Sec. 2.3.1, heavy nuclei can attain ultra high energies through magnetic sling shots inside the neutron star wind zone. The small part of nuclei, which escaped from the pulsar wind nebula, are likely to be captured by strong magnetic fields of dense regions of the OB association. Magnetic field strengths in dense molecular clouds are expected to be ~ 1 mG [195]. Thus, nuclei with E / Z ~ 1 EeV propagate attaining Bohm diffusion [193]. The resulting time delay of several thousand years [196] produces a steepening of the characteristic power law injection spectrum, E^-2, of the pulsar nebula. ⁽¹²⁾ In their random traversal of the OB association, the nuclei undergo photodisintegration on the far infrared thermal photon population and liberate neutrons.

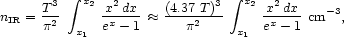(28)

where T is the kinetic temperature of the molecular cloud, x E / T, and E is the target photon energy in degrees K. The relevant photon energy range is established via standard kinematics of the photodisintegration process,

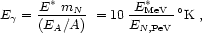(29)

where 5 < E^*_MeV < 25 is the energy region for giant dipole resonance contribution in the nucleus rest frame, and E_A / A E_{N, PeV} is the lab frame energy/nucleon. For E_{N, PeV} ~ 10³, Eq. (29) leads to x₁ = 50 / T and x₂ = 250 / T, with T in degree K. Molecular clouds with HII regions have temperatures between 15 and 100 [197], thus taking an average photodisintegration cross section of 40 mb, ⁽¹³⁾ we find that the nucleus mean free path lies between 0.80 and 380 pc. This corresponds to a reaction time between 4 to 1500 yr << time delay, alowing sufficient neutron production to explain the anisotropy [54].

The Galactic anisotropy observed by the various collaborations spans the energy range 0.8 to 2.0 EeV. The lower cutoff specifies that only neutrons with EeV energies and above have a boosted c _n sufficiently large to serve as Galactic messengers. The decay mean free path of a neutron is c _{n 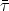n} = 10 (E_n / EeV) kpc, the lifetime being boosted from its rest-frame value 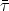_n = 886 seconds to its lab value via _n = E_n / m_n. Actually, the broad scale anisotropy from the direction of the GP reported by Fly's Eye Collaboration [51] peaks in the energy bin 0.4 - 1.0 EeV, but persists with statistical significance to energies as low as 0.2 EeV. This implies that if neutrons are the carriers of the anisotropy, there needs to be some contribution from at least one source closer than 3 - 4 kpc. Interestingly, the full Fly's Eye data include a directional signal from the Cygnus region which was somewhat lost in unsuccessful attempts [198, 199] to relate it to -ray emission from Cygnus X-3. The upper cutoff reflects an important feature of photodisintegration at the source: heavy nuclei with energies in the vicinity of the ankle will fragment to neutrons with energies about an order of magnitude smaller. To account for the largest neutron energies, it may be necessary to populate the heavier nucleus spectrum in the region above the ankle. ⁽¹⁴⁾ This is not a problem - one fully expects the emerging harder extragalactic spectrum to overtake and hide the steeply falling galactic population. It is not therefore surprising that in order to fit the spectrum in the anisotropy region and maintain continuity to the ankle region without introducing a cutoff, the AGASA Collaboration required a spectrum E^-3 or steeper [49].

For every surviving neutron at ~ EeV, there are many neutrons at lower energy that decay via n p + e^- + _e. The proton is bent by the Galactic magnetic field, the electron quickly loses energy via synchrotron radiation, and the _e travels along the initial neutron direction, producing a directed TeV energy beam [54]. The sensitivity of forthcoming neutrino telescopes to this signal is discussed in Sec. 4.2.

⁴ Even earlier ideas relating UHECRs with neutron stars can be found in Refs. [166, 167], although these attempts have failed at either reaching the highest energies, or reproducing the spectrum, or reproducing the apparent isotropy of the arrival directions of UHECRs. Back.

⁵ See [169, 170], also [171], for related research. See [172] for yet another model of UHECR generation in neutron stars, involving planetoid impacts. Back.

⁶ Note that the predicted spectrum of Eq. (22) is very flat, = 1, which would agree only with the lower end of the plausible range of observed at ultra-high energies. Propagation effects can produce an energy dependence of the confinement parameter Q and, correspondingly, a steepening of the spectrum toward the middle of the observed range 1 2. Back.

⁷ The gyroradius of these UHECRs in a Galactic field of µG strength is considerably less than the typical distance to a young neutron star (~ 8 kpc). Since the iron arrival distribution at 10²⁰ eV probes similar trajectories to protons at a few times 10¹⁸ eV, Galactic iron nuclei would show a nearly isotropic distribution with a slight correlation with the Galactic center and disk, at higher energies. Back.

⁸ A supernova that imparts E_SN = 10⁵¹ ₅₁ erg to the stellar envelope of mass M_env = 10 M₁ M is considered. Also, that the condition for iron nuclei to traverse the supernova envelope without significant losses is that 100 g cm^-2 [179]. Back.

⁹ The Parkes multibeam pulsar survey is a large-scale survey of a narrow strip of the inner Galactic plane (|b | < 5°, 260° < l < 50°, see [180] and references therein). It has much greater sensitivity than any previous survey to young and distant pulsars along the Galactic plane, and it has resulted in the detection of many previously unknown young pulsars, potentially counterparts of unidentified -ray sources, e.g. [181, 182]. Back.

¹⁰ A similar scenario would explain the anisotropy spot towards the Galactic Center [194]. Back.

¹¹ Indeed, location problems may arise as well: the PWN size (given that the TeV source size is 6 pc if indeed located at 1.7 kpc, and that the source is diffuse) would make the PWN substantially larger than both Vela's PWN (~ 0.1 pc at 250 pc) and Crab's (~ 1 pc). Additionally, if one were to associate the nearby EGRET source 3EG 2033+4118 with the putative pulsar itself, it is unclear whether the PWN hypothesis for the TeV source would imply that it is only a one sided PWN (Y. Butt, private comunication). Back.

¹² Note that once diffusion has been established, additional Rayleigh steps in the Galactic magnetic field do not change the spectral index (~ -3) significantly. Back.

¹³ The photoabsorption cross section roughly obeys the Thomas-Reiche-Kuhn sume rule, i.e., _d = 60NZ / A mb-MeV [97]. Back.

¹⁴ To produce the highest energy neutrons (with energy 10^18.2 eV) via photodisintegration of medium mass (say, A = 10 - 20) nuclei, one needs primary particles with energies 10^19.2 eV. For a falling spectrum E^-3, the medium mass nucleus population at 10^19.2 eV is roughly 3 orders of magnitude smaller than the diffuse flux at 10^18.2 eV. This means that it is about 1.6 orders of magnitude smaller than the reported CR excess (which is about 4% of the diffuse flux, see Sec. 1.3). However, since each nucleus produces roughly A - Z neutrons, the average number of liberated neutrons is on the same order of magnitude, 1.6 - log₁₀(A - Z), than the obseved neutron population at 10^18.2 eV. Back.