


Various methods have been proposed to derive a model of the
mass distribution from a given rotation curve (see
Burbidge and Burbidge, 1975
for a review). All methods are based on the principle
that, in the plane of the galaxy, there is a balance between
the force of gravity and the centrifugal force. (Pressure forces
are in general two orders of magnitude smaller than the centrifugal
forces and are therefore neglected). In this way the
observed rotation velocity at radius R, V(R) can be
related to
the radial derivative of the gravitational potential, which in turn
is related to the mass distribution through Poisson's equation.
In each of the methods a specific family of solutions of Poisson's
equation is assumed to take care of the unknown distribution of
mass in the direction perpendicular to the plane which results in
a mathematical relation between V(R) and the mass surface
density,
 M(R)
(or in some methods
M(R)
(or in some methods
 M(R), the mass volume density).
M(R), the mass volume density).
In our analysis of the rotation curves of 25 spirals we have
used two methods to derive the mass distribution for each galaxy.
The first method in the one described by
Nordsieck (1973),
the second one has been described by
Shu et al. (1971).
Nordsieck's method is based on Toomre's disk method.
Toomre (1963)
found a solution of Poisson's equation for an infinitesimally thin disk
which enabled him to relate the mass surface density to the rotation
velocity with a Fourier-Bessel integral. A solution of this
integral can be achieved by assuming
V(R = 0) = V(R =
 ) = 0, then we have:
) = 0, then we have:
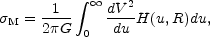 |
(2) |
where
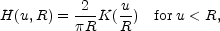 |
and
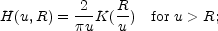 |
(3) |
K is the complete elliptic integral of the first kind. Since the
rotation curves are not known out to infinity but out to a radius
Ro an estimate has to be made for the contribution to
the integral from Ro to
 . Nordsieck has
discussed a few extreme cases of extrapolation and has worked out a
convenient compromise between a flat
rotation curve and a Keplerian one. Further, he has made an
approximation to treat the discontinuity around u = R in
H(u, R).
The resulting relation for the surface density is:
. Nordsieck has
discussed a few extreme cases of extrapolation and has worked out a
convenient compromise between a flat
rotation curve and a Keplerian one. Further, he has made an
approximation to treat the discontinuity around u = R in
H(u, R).
The resulting relation for the surface density is:
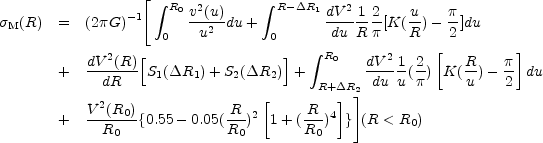 |
(4) |
In the inner parts (R < 1/2Ro) the first
term provides the
main contribution. The second, third and fourth term are small terms to
treat the discontinuity around u = R, and the fifth term
is the contribution from Ro to
 . The error in
. The error in
 M(R)
is, according to Nordsieck,
M(R)
is, according to Nordsieck,

 = 74
V1002(R)
Rkpc-1 kpc
M
= 74
V1002(R)
Rkpc-1 kpc
M pc-2, with V100 and
Rkpc in
units of 100 km s-1 and kpc respectively. For
Ro = 30 kpc and
V(Ro) = 200 km/s the error in
pc-2, with V100 and
Rkpc in
units of 100 km s-1 and kpc respectively. For
Ro = 30 kpc and
V(Ro) = 200 km/s the error in
 M(Ro) is about
10M
M(Ro) is about
10M pc-2. Note
that in Eq. (2) the derivative of V2 is required. We
have smoothed the observed rotation curve with cubic splines to
determine this derivative as accurate as possible.
pc-2. Note
that in Eq. (2) the derivative of V2 is required. We
have smoothed the observed rotation curve with cubic splines to
determine this derivative as accurate as possible.
The curve of M(R), the mass within a cylinder of radius
R, can be found by integrating
 M(i)
M(i)
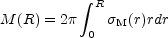 |
(5) |
Similarly, the angular momentum H(R) and the kinetic energy of rotation E(R) of the disk are given by:
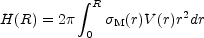 |
(6) |
and
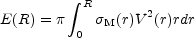 |
(7) |
The other method to determine the mass distribution we have used is the one described by Shu, Stachnik and Yost (1971). These authors used a set of one or two inhomogeneous; spheroids and a Toomre disk to fit the rotation curve. For the spheroids a mass distribution of the following form is adopted:
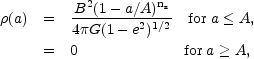 |
(8) |
where A and B are adjustable constants with the dimensions of length and angular velocity respectively, a is the semi-major axis of the spheroidal surface under consideration and ns is a free parameter that controls the degree of central concentration of the mass within the spheroid. The flattening of the spheroids, represented by the eccentricity e, can also be chosen freely. A point with cylindrical coordinates R, z lies on a spheroidal surface with semi major axis
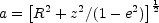 |
(9) |
For such spheroids the surface density and square of the angular speed of rotation in the z = 0 plane are given by:
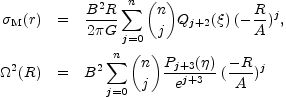 |
(10)
|
The variables  and
and  in these
expressions are given by
in these
expressions are given by
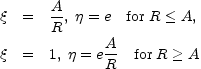 |
(12) |
The functions
Qj+1( ) and
Pj+1(
) and
Pj+1( ) are obtained
from the integrals:
) are obtained
from the integrals:
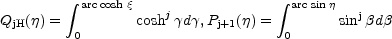 |
(13) |
which in turn can be derived from recurrence relation (see Shu et al., 1971).
The Toomre disks are a family of analytic solutions of Poisson's equation (Toomre, 1963). The surface density of the (nT)th model (nT = n + 1) in the sequence is:
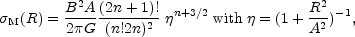 |
(14) |
and the square of the angular velocity is:
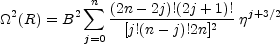 |
(15) |
A and B are again adjustable constants.
In the model fitting program (kindly provided by Dr. F.H. Shu)
the parameters A, ns and e are
specified; a least squares fit to
the observed rotation curve yields B. It turns out that for late
type galaxies the rotation curve can be fitted with a Toomre disk,
for earlier type galaxies we had to add one or two spheroids in the
inner parts. We have tried to diminish the number of parameters by
taking nT = 1 and
ns = 5, for the eccentricity we used
either e = 0.866 or e = 0.98. Comparison with the method
of Nordsieck shows that the resulting
 M(R)
are in good agreement (usually to
within 10%, or better). The fitting method provides us with a
measure of the total mass in the galaxy out to infinity. Such a
number has perhaps little value in itself but it allows us to
estimate the minimum mass outside Ro compatible with
the observed
rotation curves and the assumption of a well-behaved galaxy
(i.e. a galaxy with a smoothly declining mass distribution and a finite
total mass).
M(R)
are in good agreement (usually to
within 10%, or better). The fitting method provides us with a
measure of the total mass in the galaxy out to infinity. Such a
number has perhaps little value in itself but it allows us to
estimate the minimum mass outside Ro compatible with
the observed
rotation curves and the assumption of a well-behaved galaxy
(i.e. a galaxy with a smoothly declining mass distribution and a finite
total mass).
We have made no attempt to incorporate a massive halo in the analysis. If such haloes are present at all, their properties are unknown. One might try to determine the properties of both the disk and a halo component, but then further assumptions are necessary, e.g. a constant M / L for the disk. For most of the galaxies in our sample no unambiguous results concerning the distribution of the various stellar populations in the disk are available to justify the assumption of a constant M / L ratio. Unless some of the properties of the disk and the halo component can be inferred from other data, e.g. properties of the nonaxisymmetric perturbations like spiral arms, no simple solution to this problem suggests itself.