6. The relationship with morphological types

In the foregoing sections we have already touched upon the correlation of a number of physical properties with morphological type. We will now discuss the available information, in particular the question whether there is a one-to-one correspondence between morphological type and one or more physical properties.

We have found that for each galaxy log M(R) is roughly proportional to log R, but galaxies with different rotation velocities, as measured by V_m, have a different constant of proportionality. This indicates that the global mass distribution in spiral galaxies is similar, but galaxies with large V_m are more densely packed than galaxies with small V_m. The difference in Hubble type is not evident from the curves of M(R): for example the Sab galaxy NGC 4151 has about the same M(R) curve as the Sc galaxy NGC 3198. This seems to imply that the Hubble type is mainly determined by differences in the local distribution of matter. It is necessary to assess the influence of V_m first, before discussing Hubble type differences. Note that V_m is loosely correlated with L_B and hence connected with Van den Bergh's luminosity class, but that a precise distinction of e.g. luminosity class I, I-II and II in terms of different values for V_m is impossible.

The mass-to-luminosity ratio, both the global one and its radial distribution, does not correlate well with Hubble type. The ratio of the surface densities of total mass and HI gas mass in the outer parts of galaxies correlates better with V_m than with Hubble type. There is, however, a striking difference in these ratios in the inner parts of galaxies of different types. Crudely speaking the ratio of total mass to HI gas mass in the central regions is decreasing towards later types. This is the only clear correlation between morphological type and the physical properties we discussed so far.

Two effects reinforce each other to produce the above correlation: in early type spirals there is a stronger increase in _M(R) and a stronger decrease of _HI(R) towards the centre than in late type galaxies. Unfortunately, both these quantities cannot be reliably determined for most of the galaxies in our sample because of beam smoothing effects (cf. chapter 3 and 6). Although we have corrected the 21 cm rotation curves in the inner parts of a number of spirals with optical data we could not do this correction properly for galaxies with large nuclear bulges. For the influence of beamsmoothing on the radial distribution of HI gas we cannot correct at all. This greatly restrains the discussion of the relation between Hubble type and the gas-to-mass ratio in the central parts. In about 50% of the number of galaxies in our sample the resolution in the inner parts is insufficient.

We have investigated whether the shape of the curves of _M(R) show a relation with morphological type. In general these curves have a peak in the centre and decrease roughly exponentially outward. The amplitude of the central peak decreases towards later type, as can be seen in Fig. 3 of chapter 6. It is difficult to make this statement more quantitative. We have tried several ways to do this, but none of them is very satisfactory. The main difficulty is that we have to find suitable normalization factors, both for the surface density and the radial coordinate, otherwise we cannot compare galaxies with different V_m. We have tried to normalize the _M(R) curves by scaling them in the radial direction with the radius at which _M = 50 M pc^-2. It turns out that there is still a substantial variety in the slope of the quasi-exponential part of these scaled curves, thus preventing a consistent procedure to measure the amplitude of the central peak above the disk. We can, however, make estimates from the fits we made to the rotation curves with the spheroids and disk models. In Fig. 13 we show the percentage of mass in the spheroids as function of Hubble type and Yerkes form. Only a loose correlation exists. We have listed other quantities, like the ratio of central surface density to central disk surface density, again determined from the model fits, in Table 3.

Figure 13. Relative mass in the spheroids (Msph / Mfit) vs Hubble type (left) and Yerkes form class (right). Pluses represent galaxies for which the resolution in the inner parts is poor, dots represent galaxies for which the resolution in the centre is adequate or for which a correction has been made with optical data.

Table 3.

Galaxy	Hubble type	Yerkes form	relative mass in spheroid % of Mf	log o / do	log M / HI	Rmax/Ro	-curve	beam correction†
N3718
M81	ab	k	2.9	0.67	> 4	0.32	3.6	no
N4151	ab	gk	10.1	1.88	3.6	0.01	15.7	yes
N4736	ab	g	14.9	1.49	> 4	0.06	10.2	yes
M31	b	k	12.7	1.67	3.9	0.07	10.3	yes
N891	b	gk	10.0	0.55		0.25	3.6	no
N2841	b	k	13.9	1.41	> 4	0.14	8.7	no
N4565	b	gk	13.4	1.13		0.11	6.0	no
N5383	b	fg	14.9	1.11		0.22	5.3	no
N4258	be	g	7.7	1.16		0.10	7.4
N5055	be	g	19.0	1.80	2.8	0.05	24.9	yes
M51	be	f	6.5	0.40	2.4	-	2.6	-
N7331	be	gk	7.8	1.18	2.7	0.13	9.3	yes
N253
N3198	c	af	0	0	2.2	0.35	3.5
N3359
N5033	c	g	9.4	1.47	2.9	0.06	11.7	yes
N5907	c	g	10.2	0.76		0.19	5.4	no
N7640
N300
M33	cd	f	0.89	0.49	2.1	1.0	2.6
I342			11.5	0.73	2.4	0.35	4.4	no
N2403	cd	af	6.2	0.45	1.9	1.0	3.0
N4244	cd	a	2.1	0.17		0.58	2.9	no
M83	cd	fg	12.2	0.62		0.26	-	no
M101	cd	f	4.7	0.46	2.6	0.60	2.7
N6946
N2805
N4631	d	af	12.6	1.21		0.08	8.9	no
N4236	dm	a	0	0		0.90	2.1
I2574
N3109			0	0		0.75	2.2
HoII
N4449
Galaxy			5.7	1.32			13.6
† if not indicated correction for beamsmoothing is not necessary.

One of these is the parameter

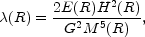which can be calculated from the curves of the cumulative mass, M(R), angular momentum, H(R), and kinetic energy of rotation, E(R). (R) varies from 0 in the centre to 0.33 ± 0.01 for 22 of the 25 galaxies in our sample. The exceptions are M51 (strange rotation curve), M33 (the rotation curve we used does not extend beyond a turnover radius) and M83 (rotation curve comes from one of the artificial models described by Hunter and Toomre (1969). Although we cannot exclude the possibility that the constant value of (R) is an artefact of the approximations implicit in the mass model calculations, the curves of (R) do represent a smooth transformation of the rotation curves. The shape of the (R) curves is different for different galaxies: for early type spirals (R) rises steeply to about 0.25 and slowly increases over the main disk, and for late type small galaxies (R) increases almost linearly. Late type large galaxies have a curve of (R) intermediate between that of early types and late type small galaxies. In Table 3 we have included a column which gives this information in a quantitative form: there we present the ratio of radii

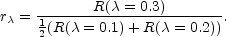A problem with the further interpretation of the (R)-curves is the dependence on R_o: if we scale the radial coordinate with R_o to achieve a uniform representation we find that e.g. for NGC 2841 r = 3.8 if R_o = 7' and r = 8.7 if R_o = 14'.

This dependence of possible type indicators on R_o is also present in the other quantities listed in Table 3. For instance, in the mass model fits the Toomre disk is fitted first, and for the nearly flat rotation curves the turnover-radius associated with this disk had to be taken close to R_o in order to achieve a good fit. It is therefore difficult to find a good criterion for making an ordering of the galaxies in terms of a dynamical sequence. Nevertheless, there are weak indications that there is not a unique correspondence of Hubble type or Yerkes form with the dynamical type indicators we have investigated. From Table 3 we can see that if we use central mass concentration (log_o / _do where _o is the central surface density and _do the central surface density of the Toomre disk) as a criterion to form a dynamical sequence we have in order of log_o / _do : NGC 4151 (Sab, gk), NGC 5055 (Sbc, g), M31 (Sb, k), NGC 4736 (Sab, g), NGC 5033 (Sc, g), NGC 2841 (Sb, k), NGC 4631 (Sd, af), NGC 7331 (Sbc, gk), NGC 4258 (Sbc, g) and so on. This list contains 5 Hubble stages and 4 Yerkes form classes and these occur not in their proper sequence. We get more or less the same list if we use the shape of the (R)-curve, or even the quantity R_max / R_o, where R_max is the radius where the rotation curve becomes roughly flat, as the ordering criterion.

From the above discussion we conclude for the moment that the morphological stages do not have a one-to-one correspondence with the physical quantities we can derive from 21 cm line data. Only the loose correlations, found already in studies of the integral properties, are found back. In that respect we must emphasize that correlations derived from integral properties cannot be interpreted in a straightforward way. For this it is necessary to assume an "ideal form" of the radial distribution of matter. An interesting result like the correlation between the shape of the integral HI profile and Hubble type (Shostak, 1977) is not easy to translate into a statement about the shapes of rotation curves and the forms of the distribution of _HI in galaxies of different morphological types. This can be illustrated by considering Shostak's data for those galaxies for which a Yerkes form class is available. The shape of integral HI profiles is usually characterized by two peaks at either side of the systemic velocity. The peak-to-centre ratio, p, can be estimated by averaging the amplitude of the two peaks and dividing it by the amplitude at the systemic velocity (see Shostak, 1977 for details). In Fig. 14 we show p as function of Yerkes form for different Hubble types. p is apparently better correlated with Hubble type (cf. Shostak's Fig. 1, and the separation of symbols in Fig. 14) than with Yerkes form, despite the good correlation between 4 these two classification systems. This result illustrates also that no simple one-to-one correspondence exists between the morphological types and physical quantities derived from 21 cm line data.

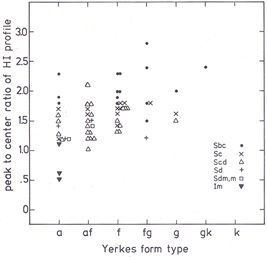Figure 14. Peak-to-centre ratio of the HI profile vs. Yerkes form for the galaxies in the sample of Shostak (1977). The various symbols represent different Hubble types.