Almost any feature in the SED of a starburst galaxy could, in principle, be used as a star formation rate (SFR) indicator, provided the appropriate bolometric correction can be worked out. In many cases, however, this is by no means a trivial exercise. Here we briefly discuss some of the more commonly-used techniques to determine the SFR in galaxies. Others exist (for example, the X-ray flux), but these are not yet sufficiently well understood from a theoretical point of view to warrant inclusion here.
The optical / UV continuum For those techniques which depend upon optical or UV data e.g. [14], the effects of dust obscuration in and around the star-forming regions are particularly severe, and make it mandatory that we understand the dust attenuation physics, which is discussed extensively by Fischera here [37]. In principle, provided that the initial mass function (IMF) is invariant, the intrinsic UV luminosity should scale directly as the star formation rate. From stellar spectral synthesis models, the star formation rate is given in terms of the 1500Å flux by [49, 67]:
 |
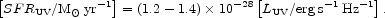(1) |
The far-IR continuum The use of the far-IR emission from warm dust associated with the star formation region may provide a more reliable estimate of the SFR [31, 40]. However, star formation rates derived in this way most frequently assume that the dust is effectively acting as a re-processing bolometer wrapped around the star forming region, and that cool and old stars do not provide too much of a contribution.
In any real galaxy, old stars exist, and the stars are neither unobscured by dust, and nor are they totally obscured [69]. This degree of obscuration is one of the many "geometrical" factors which render the derivation of the absolute SFR quite uncertain. For example, [45] includes a number of these geometrical factors in the following formula for the IR luminosity of a galaxy:
 |
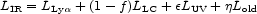(2) |
This allows a fraction, (1 - f ), of the ionizing flux to be
absorbed by dust in the HII region, assuming that
all of the
Lyman-
photons are
multiply scattered by the gas and ultimately absorbed by dust in the
surrounding HI region, that a fraction,
, of the
non-ionizing UV photons are absorbed, and that a fraction
of the
radiation field produced by the old stars is also absorbed by
dust. Photoionization models of HII regions show
that, typically, the
Lyman- flux is of order
30% of the total stellar flux absorbed by the nebula, so that globally,
the dust is fairly efficient in capturing and re-radiating the flux
originally radiated by the star in the Lyman continuum.
The dust obscuration is observed to increase both with galaxian mass
[53],
and with the absolute rate star formation
[12,
1,
23,
88].
This can be understood as the combination of the degree of chemical
evolution of the interstellar medium, which leads to a low dust to gas
ratio in dwarf galaxies, and of the operation of the Schmidt Law
[74]
of star formation, which couples the star formation rate per unit area
to the gas surface density, and therefore, for a given dust to gas
ratio, to the dust obscuration, provided that the surface rate of star
formation is coupled to the global rate of star formation, which appears
to be most often the case. Recent data
[49,
64]
gives 
SFR
gasn, with n ~ 1.3 - 1.6 .
The radio continuum The radio continuum has also been used as a star formation rate indicator. Observationally, there is an extraordinarily close correlation between the 60 µm infrared continuum and the radio 1.4 GHz continuum of star forming galaxies. This linear correlation spans ~ 5 decades of magnitude with less than 0.3 dex dispersion [92, 91]. The mean relationship between the 60 µm flux and the 1.4 GHz continuum is:
 |
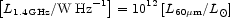(3) |
In star forming galaxies at 1.4 GHz, the non-thermal emission by relativistic electrons dominates by at least an order of magnitude over the free-free emission [16]. Therefore, and somewhat remarkably, this relationship couples a purely thermal process with a non-thermal process, over many decades of flux, and locally, within individual galaxies.
If the lifetime of the synchrotron electrons is short compared with the evolution timescale of the starburst, then as [10] have shown, the synchrotron emissivity acts as a bolometer of the supernova rate. This works because the relativistic luminosity is ultimately derived from the Fermi acceleration process in supernova shocks, which for constant efficiency should be proportional to the star formation rate. Specifically, the non-thermal luminosity is given by:
 |
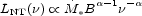(4) |
where 
* is the total
star formation rate. Since the observed spectral index lies in the
range,
0.5 > > 1.0,
there is only a very weak dependence on the magnetic field in this
case. To the extent that the FIR luminosity is providing a bolometric
indication of the SFR, this seems to provide the most natural
explanation of the FIR : radio correlation in starburst galaxies. This
will be especially true when the pressure in the interstellar medium is
high, since provided that the magnetic pressure is in equipartition with
the gas pressure, the synchrotron losses are strongly encouraged by the
high interstellar magnetic field.
Recombination emission lines
A fairly direct and extensively-used technique is to measure hydrogen
recombination line fluxes. Provided that the HII
region can absorb all the EUV photons produced by the central stars,
this should be a reliable technique, since in this case the flux in any
hydrogen line is simply proportional to the number of photons produced
by the hot stars, which is in turn proportional to the birthrate of
massive stars. This relationship has been well calibrated at solar
metallicity for the
H line. In units of
M
yr-1, the estimated star formation rate is given by
[26,
49,
67]:
 |
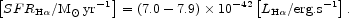(5) |
Provided that the star-formation regions are resolved, their Balmer
decrements can be used to estimate the absorption in any foreground dust
screen. However, it is possible that some star forming regions are
completely obscured, even at
H. This problem can be
avoided by observing at infrared wavelengths, in
Br, for example. A
further complication is that the dust content of the nebula is
metallicity-dependent, and therefore an appreciable fraction of the
hydrogen ionizing photons may be absorbed by dust in high metallicity
HII regions. This possibility, first seriously
quantified by
[68],
has been discussed by a number of authors since and its effect has been
investigated and quantified (as far as is possible by direct
observation) in a series of recent papers by Inoue and his collaborators
[43,
42,
44].
Dopita [24]
has shown that this effect increases in importance in the more compact
HII regions, and may lead to errors as high as ~
30% in estimates of the global SFR. Indeed, in ultra-compact HII regions, as much as ~ 90% of the ionising photons
may be lost to dust in the ionized nebula. However, the magnitude of
this effect is a function of the product of the metallicity, Z
and the dimensionless ionization parameter,
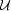, both of which can in
principle be determined by emission line diagnostics.
[OII] emission lines
The Balmer lines shift out of the visible range by z >
0.4. The other strong emission lines accessible at higher redshift are
the [OII] and [OIII] lines. Of
these, the [OIII] lines are known to be very
sensitive to the ionization parameter, and therefore the
[OII]
3727, 9Å lines
have been used of necessity to try to estimate the SFR for galaxies
lying in the redshift range
z ~ 0.4 - 1.5. Photoionization models show that these are by no
means ideal as star formation indicators, because their strength not
only depends on the attenuation, which tends to be large in the UV, but
also on the metallicity of the ionized gas. These may lead to large
discrepancies between SFR estimated from
H and from the
[OII] lines
[15].
However, Kewley and her collaborators
[54]
have developed techniques to allow corrections for both metallicity and
reddening which bring the results of these two emission line techniques
into much better agreement (see also the paper by Kewley, elsewhere in
these proceedings).