3. PHYSICAL ELEMENTS OF SED MODELLING

A successful model for the SED of a starburst galaxy must bring together in one package a wide range of physics including the structure evolution and atmospheric models of stars, the full physics of ionized plasmas, a realistic dust model and a certain amount of molecular physics. In addition, the geometry of the dust with respect to the stars is fundamental in determining the shape and peak of the far-IR re-emission, as discussed by Popescu & Tuffs (this volume). Ideally we should seek to develop an understanding of the geometry from the constraints offered by the other physics of the problem. Finally, the radiative transfer problem must be solved for the complex multi-phase nature of the interstellar medium. Few, if any, models have all these physical elements included at the same time.

Stellar Spectral Energy Synthesis   There are a number of publicly available codes which give consistent results on the SED of the stellar component, for whatever choices of the IMF are preferred. These include the Starburst 99 code of Leitherer [59], the Pégase code [34], the Bruzual and Charlot code [11] and the code by Kodama & Arimoto [48]. These codes differ mainly on their predictions in the EUV, since here they rely on theoretical atmospheric and mass-loss models in which a good deal of progress has been made recently. In this respect the Starburst 99 code is probably the state of art [78]. The major strength of the Bruzual and Charlot code is in the synthesis of the older stellar populations.

Ionized Gas Physics   For the ionized plasma, two major codes have been used in SED modelling, the Cloudy code [33], and the Mappings III code [83, 20, 21]. Both of these include all relevant gas-phase physics and a complete model for the absorption and re-emission of radiation by dust grains in the nebula. These codes provide both the emission line SFR diagnostics discussed above, as well as giving estimates of both the chemical abundance and the ionization parameter in the ionized gas [20, 52]. The ionization parameter provides us with an independent physical constraint on the geometry of the gas and dust with respect to the central stars.

Grain Composition and Size Distribution Most models use a dust model consisting of both a carbonaceous and silicaceous component. Apart from composition, the grain size distribution and the grain composition are the principal factors which determine the wavelength-dependence of the absorption and scattering processes. Most models use a grain size distribution and a composition which yield results consistent with observations of the extinction curve, and which also attempts to match the constraints on the cosmic abundances of the atomic species locked up the the grains in local and Magellanic Cloud environments. Examples include the older Désert et al [19] the more recent Weingartner & Draine model [89, 90] or the models of Dwek and his collaborators [32].

The far-IR re-emission process depends critically on the grain size distribution, since small grains are subject to large stochastic variations of temperature [60, 27]. Most codes take this effect into account when computing the far-IR spectrum. The grain size distribution in the ISM results from the balance between the grain formation and destruction processes. It has usually [63] been represented by a power law over a wide range of sizes, a;

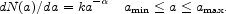(6)

where , a_min and a_max are derived by an empirical fit to the scattering and extinction in the local ISM. A more complex distribution has been suggested on physical grounds [89], and this takes into account both silicate and carbon-containing grains with different grain-size distributions. For the carbonaceous grains, the polycyclic aromatic hydrocarbon grains (PAHs) are treated as providing an additional component on a continuous distribution of grain sizes. Even these distributions can be approximated by power-laws over a wide range of radii.

Grain shattering has been shown to lead naturally to the formation of a power-law size distribution of grains with ~ 3.3 [47], observationally indistinguishable from the MRN value, ~ 3.5. Such a grain size distribution can also hold only between certain limits in size,the smaller size being determined by natural destruction processes such as photodestruction, and the upper limit being determined by limits on the growth by condensation and sticking. To capture these elements of the physics, Dopita et al [25] have adopted a modified grain shattering profile with the form;

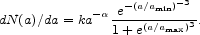(7)

Although it is certainly true that the size distribution is a function of the environment, it is very dangerous to make the grain size distribution a free parameter, since this could enable one to fit the far-IR emission peak with entirely the wrong geometry of the gas with respect to the stars. It is better to take the approach pioneered by Dwek, and use the constraints offered by the UV attenuation by the dust simultaneously with fitting the far-IR peak. However, in such an exercise we must also take account the turbulent fractal structure of the ISM dust screen, which provides a greater than expected opacity in the IR, but which gives a smaller than expected attenuation in the UV, see Fischera [35, 36, 37].

Grain Destruction   Since, in this conference, the possibility that environmental effects change the nature of the grains, the grain size distribution, and the relative abundance of the PAH molecules has been discussed at some length, let us now consider these issues. The life-cycle of dust grains in the interstellar medium must, in large measure, represent a balance between grain destruction and shattering in the fast shocks found in the hot and warm phases of the ISM, and the processes which build up grains in the dense molecular clouds. Dust evolution therefore depends upon the mass transport between these various phases. The presence or absence of the dust grains in a particular environment can be inferred by a measurement of elemental depletions in the interstellar medium.

Dwek & Scalo [30] and McKee [61], have developed the evolutionary equations which describe these processes. These are simplified here. Let M be the mass of a particular grain-forming element in the ISM, and suppose a fraction of this element is locked up into dust in the interstellar medium. In the hot phase, the evolution of will depend on the characteristic timescale needed to destroy the grains in the (warm) low-density phase through supernova explosions, _SNR, the timescale needed to regenerate the dust in the cold dense phase _form, and the time taken to transport the dust from the (cold) dense to the (hotter) less-dense phase, _{C H}. Assuming that the growth time of dust grains in the cold phase is very short compared with the timescale of mass transport between the cold and warm phases (or its inverse), the dynamical evolution of the dust mass in the hot phase is:

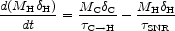(8)

and in equilibrium;

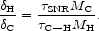(9)

In other words, the difference in the dust fractions between the two phases depends simply on the relative size of the reservoir of dust in the cold phase and ratio of the time taken for the dust to escape into the hot phase to the time taken to destroy it in the hot phase.

Now, what determines the timescale of destruction _SNR? This is the mean interval between the passage of fast shocks which result in sputtering of grains or in the destruction of PAH molecules. The sputtering rate is a rather complex function of temperature, and threshold energy [28] but can be rather well fitted by an equation of the form [29]:

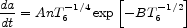(10)

where T₆ is the gas temperature in units of 10⁶K and A and B are constants. For graphite, A = 6 × 10^-6 µm yr^-1 and B = 3.7 while for silicate A = 1.8 × 10^-5 µm yr^-1 and B = 4. The sputtering lifetime for average size grains (a ~ 0.1 µm) is of order 10⁵ years in fast shocks. This is comfortably shorter than the grain braking timescale, so that only the very largest grains can survive. Depending on the magnetic field configuration, grains start to be destroyed (rather than simply shattered) in shocks faster than 100 km s^-1, and the process is complete by ~ 400 km s^-1.

How often do shocks this fast pass through the warm phase of the interstellar medium? We can estimate this by asking at what size and shock velocity do supernova remnants become dominated by cooling, after which they rapidly slow down. The end of the adiabatic (Sedov-Taylor) phase is signalled by the cooling timescale in the shell becoming less than the dynamical expansion timescale; _cool < _dyn. The cooling timescale in a strong shock can be approximated [22] by:

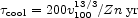(11)

where v₁₀₀ is the shock velocity, v_s, in units of 100 km s^-1, the chemical abundance Z is with respect to solar, and the pre-shock density is n cm^-3. The Sedov Taylor solution for the SNR expansion gives:

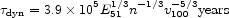(12)

were E₅₁ is the kinetic energy of the explosion in units of 10⁵¹ ergs. Therefore, we can infer that the SNR becomes radiative when:

(13)

This is interestingly close to the velocity at which sputtering and grain destruction is complete. The radius at which this condition is met is found by noting that t = 2R / 5v_s and using this to eliminate time in the Sedov equation for the radius:

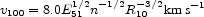(14)

where R₁₀ is the radius in units of 10 pc. Thus, from eqns. 13 and 14 we have that the SNR becomes radiative when:

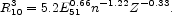(15)

In a disk-like galaxy, the gas with surface density _g M pc^-2 is confined within twice the scale height, H. The surface rate of supernova events is proportional to the surface rate of star formation, _{SNR SFR}, and the observational Schmidt Law [49, 64] gives _{SFR gas}^1.4. These relationships appear to hold in the case of starburst galaxies as well. Thus the timescale for the gas to be processed through a supernova shock is:

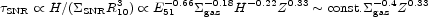(16)

because, in a self-gravitating layer, the scale height is set by the velocity dispersion of the disk gas in the vertical plane, v_z, giving H = v_z² / G _gas, and in disk galaxies the observed HI vertical velocity dispersion is observed to be almost constant at between 7 and 10 km s^-1 [87, 76, 55, 75]. In disk galaxies, as _gas decreases with increasing radius, so does Z, and therefore the two terms in eqn. 16 almost cancel each other, giving the final result that _SNR ~ const.

The fact that the SN processing timescale is virtually constant is a remarkable and perhaps even a counter-intuitive result. It may be giving us a profound clue about the process of self-regulation of star formation in galaxies. Since the supernovae act to turbulently stir the ISM, and since the ISM density structure is thought to originate from the turbulent cascade of energy from large scales to small scales, and since this turbulent cascade is thought to set up the conditions for new star formation, then the Schmidt law itself may simply be the expression of this turbulent cascade process with constant _SNR.

Return now to the effect that this has on the grain population. It is clear from equation 9 that, if the SNR rate is also determining the timescale of large-scale mixing, and therefore the mass-exchange rate between the various phases, the ratio of the two timescales may not change much with environment. Therefore if we are to deplete the dust fraction in the hotter phase, we must rely on decreasing the mass fraction of the cold phase relative to the hotter phase as a function of environment.

PAH Physics   The PAH molecules having a molecular weight similar to coronene (C₂₄ H₁₂), are very important in absorbing UV photons, and fluorescing in the IR in a number of strong and broad emission line features in the wavelengh range between 3.29 µm and 20 µm . Being carbonaceous, and somewhat graphitic in their molecular structure, the PAH molecules have strong absorption in the 2175 Å band. The absence of this absorption feature in the attenuation curve of the light of starburst galaxies [14]. as well as the relative weakness of the IR PAH features in some starburst galaxies such as Arp220 may be evidence of the photodestruction of PAH molecules in environments with a strong UV or EUV field.

This is supported by observations in our own galaxy. Where detailed measurements have been made of the distribution of PAH emission within compact HII regions, it is found that the PAH avoids the ionized regions, and is instead found in a narrow zone of emission (the photo-dissociation region) beyond the outer boundary of the ionized gas [13]. This is clear evidence that PAH molecules cannot survive for significant lengths of time in the hostile environment in the ionized zones of an HII region. This is to be expected, because the photodissociation timescales in this region are very short. However, PAHs can survive, and are excited into emission in the photodissociation regions (PDRs) outside the ionized HII region.

The physics of the photodestruction process is rather uncertain, and so this leads to uncertainties in the form of the SED where the PAH features are strong. The most likely destruction process is by PAH charging. The electrons associated with the benzene rings are relatively easy to remove. Removal of the first causes buckling of the C-C skeleton with strong 6.2 µm and 7.7 - 7.9 µm skeletal deformation bands and both a broadening and change in relative intensities of the other IR emission features. Indeed, charged PAHs are an essential feature of any model which can reproduce the observed PAH IR emission spectrum. Most models use the "astronomical" PAH absorption properties (based largely on the measured properties of coronene) by Li and Draine [60]. PAH photodestruction appears to be caused by removal of two or more electrons, which requires photons harder than about 14eV. Thus, the simplest PAH destruction model model is that the presence of hard photons leads to rapid photodissociation in the ionized gas. In this case, the PAHs are destroyed in the ionized gas and their C is returned to the gas phase. Evidence for this can be adduced from the fact that, in HII regions [39], the measured gas-phase log[C/O] has its solar value at solar log[O/H], using the new solar abundances [7, 4, 5]. This argues for the complete photodestruction of C-containing grains in HII regions.

A somewhat more sophisticated approach might be to say that PAHs are destroyed whenever the absorption weighted mean radiation field (not necessarily ionizing) results in a photodissociation timescale which is short compared to the residence time of the PAHs in that radiation field. In this case we would compare photodissociation timescales with dynamical timescales to obtain a criterion for survival.

A third approach posits the possibility that photodissociation (by the ejection of an acetyleneic group) is countered by repair through accretion of carbon atoms [2, 3]. However, such a repair mechanism could only occur in photodissociation regions, not in the ionized gas where such groups would be rapidly photo-dissociated.

An ISM/Dust Model for Starburst Galaxies   We [25] have used a grain shattering profile of the form of eqn. (7) with both graphitic and silicaceous components. The grain size limits for both graphitic and silicaceous grains are set to a_min = 0.004 µm and a_max = 0.25 µm . The somewhat smaller size cutoff than the MRN distribution provides a stronger dust re-emission continuum below 25 µm , which is required to fit the observed IRAS colors of starbursts [72]. The constant k is determined by the total dust-to-gas mass ratio, which is determined by the depletion of the heavy elements onto dust. Our models use a solar abundance set as modified by the latest abundance determinations [4, 5, 7, 8]. The depletion factors are those used by [20] for starburst and active galaxy photoionization modeling and are similar to those found by [46] and [73] in the local ISM using the UV absorption lines to probe various local lines of sight.

When present, the PAHs are set at an abundance which uses 110ppm of Carbon. Consequently, the carbonaceous grain component is present at only rather low abundance; equivalent to 69ppm of Carbon. The PAHs are assumed to be destroyed whenever there are appreciable numbers of photons with energies greater than 14.5eV present, i.e. effectively throughout the ionized portions of the HII regions. This is all consistent with the observed C/O and O/H measurements of gas-phase abundances in HII regions in the UV made by Garnett et al. [39] for which both the C/O and O/H ratios agree with their solar values on the new solar abundance scale. This indicates that the depletion factor of C in the ionized gas is similar to that of O, which is known to be small.

The destruction of PAHs in the ionized and diffuse phases of the ISM will largely remove the 2200Å bump from the UV attenuation curve. In order to compute this attenuation we have to take account the turbulent fractal structure of the ISM dust screen see Fischera [35, 36, 37]. The cloudy fractal nature of the foreground screen flattens the attenuation curve relative to the extinction curve (which we cannot in any case observe in starburst galaxies, since we cannot make measurements of the extinction in lines of sight to individual stars). When this is done, our grain model provides an excellent fit to the Calzetti [14] attenuation curve (see Fig 1). This curve has been derived empirically from an ensemble of observations of starburst galaxies, and which has been widely used in the literature.

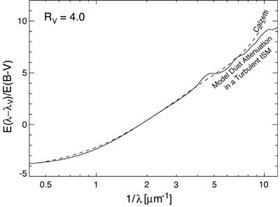Figure 1. The interstellar dust attenuation curve computed for our dust model and for a turbulent ISM with a log-normal density distribution (Dopita et al. 2004 [25]) (solid line) is compared with the empirical Calzetti attenuation curve derived for starburst galaxies. The two are identical within the errors.

In the semi-empirical modelling of Dale and his collaborators ([17, 18], and this conference), the SED of disk and starburst galaxies were suggested to form a one-parameter family in dust temperature. This suggested that starburst galaxies have hotter dust temperatures. Lagache et al [58] (again empirically) have suggested that the luminosity controls the form of the SED. Both of these may be true to some extent, since IR luminous galaxies have greater rates of star formation.

The French group [38] take the simplest approach of approximating the starburst by a spherical HII region and clumpy dust shell around the central star forming region. A more sophisticated approach is taken in the GRAZIL code by the Padova/Trieste group [77, 41, 67]. Their starburst model uses a spherical geometry with King profiles, and they allow for the formation of clusters of stars in molecular complexes, and their subsequent escape from these regions.

In the rather sophisticated models of Takagi et al [84, 85], a mass-radius relationship for the star formation region of r_i / kpc = (M / 10⁹ M)^1/2 is adopted along with a stellar density distribution given by a generalised King profile. The parameter is a compactness parameter which expresses the degree of matter concentration, and is related to the optical depth of the dust through which the starburst region is seen. For a sample of ultra-luminous starbursts, they find that, while most conform to a constant surface brightness of order 10¹² L kpc^-2, there are a few objects with surface brightnesses roughly ten times larger than this, which they ascribe to post-merger systems.

In a starburst, the individual stars form in clusters at the cores of dense molecular complexes, and initially the geometry of the gas with respect to the dust is determined by the evolution of the mass loss bubble / HII region around individual clusters. It is only at later times that these bubbles may link up to create a large-scale HII region complex driven by collective effects. In dense starbust regions, the shape of the SED is therefore determined more on the scale of individual HII regions, rather than on a galaxian scale. The size of each HII region is therefore a function of both the mass of the central cluster and its age. To provide the correct geometry, we therefore need to understand the time evolution of individual HII regions. An attempt to do this was recently described by Dopita et al. [25], and this work forms the basis of the following section.