


In what follows, one should be aware that the problem of the evolution of the size of HII regions in the interstellar medium is by no means trivial. Although we will assume that the ISM is uniform, and of a uniform pressure, such is certainly not the case in real objects. The turbulent multi-phase structure of the ISM profoundly modifies the evolution of HII regions. An attempt to model this, by evolving a source of uniform mass-loss in an isotropic log-normal density distribution (which mathematically approximates to the structures produced in a turbulent medium) is shown in 2. Such models will be required in future modelling. For the time being, let us consider on the case of uniform pressure and density in the ISM.
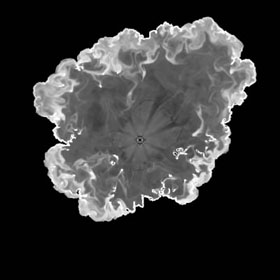 |
Figure 2. The radiative structure of a 2-D radiative mass-loss blown bubble evolving in a turbulent ISM with a log-normal density distribution having a mean atom density of unity. This has been computed using the PPMLR code developed by [82]. It shows a number of features seen in real HII regions such as elephant-trunk clouds, and demonstrates how different is the evolution compared to the case of a uniform density medium. In a log-normal density distribution, the HII mass-loss bubble expands more rapidly than in a uniform medium, and it leaves a number of high emission-measure regions having relatively high dust temperatures close to the exciting star(s). |
The work of Dopita et al. [25] drew on the theory of the size distribution of HII regions by Oey & Clark [65, 66]. In this, the HII regions expand and evolve as stellar mass-loss and supernova driven bubbles for as long as their internal pressure exceeds the ambient pressure in the ISM. When this condition is no longer met, the HII region is assumed to "stall". Of course, on reaching the stall condition, the HII region does not abruptly stop expanding, but a momentum-conserving expansion continues until interstellar turbulence destroys the integrity of swept-up shell. The time taken to reach the stall radius turns out to be proportional to the stall radius, and the mass of the OB star cluster is important in determining the stall radius; HII regions with low mass clusters stall early and at small radius for a given pressure or density in the ISM.
The radius R and internal pressure, P, of a mass-loss pressurised HII region are given by [65, 66];
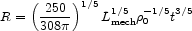 |
(17) |
and
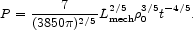 |
(18) |
Here, Lmech is the mechanical luminosity of the mass-loss
from the central stars,
 0 is
the density of the ambient medium and t is the time. The
particle density is given in terms of the ambient density by n =
0 is
the density of the ambient medium and t is the time. The
particle density is given in terms of the ambient density by n =
 0
/ µmH, and the ambient pressure
P0 = nkT0. Eliminating t
between equations 17 and 18, and setting P = P0
we obtain the following conditions for stall:
0
/ µmH, and the ambient pressure
P0 = nkT0. Eliminating t
between equations 17 and 18, and setting P = P0
we obtain the following conditions for stall:
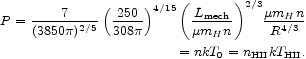 |
(19)
|
Ionization Parameters
Equations 19 and 20 imply that, for any given pressure in the ISM, all
stalled HII regions have a common ratio of
Lmech / nHII
R2. To the extent that
N*
 Lmech, where N* is the flux
of ionizing photons from the central stars, then all stalled
HII regions will be characterized by a common
value of the ionization parameter,
Lmech, where N* is the flux
of ionizing photons from the central stars, then all stalled
HII regions will be characterized by a common
value of the ionization parameter,
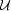 =
N* /
4
=
N* /
4 cRin2 nHII. This
ionization parameter is very important in the theory of
HII region spectra since it is one of the three
parameters which determine the emission line spectrum of the
HII region. The other two are the input spectrum
of the exciting star(s) and the gas-phase metallicity.
cRin2 nHII. This
ionization parameter is very important in the theory of
HII region spectra since it is one of the three
parameters which determine the emission line spectrum of the
HII region. The other two are the input spectrum
of the exciting star(s) and the gas-phase metallicity.
In fact, even for HII regions which are not
stalled, there is a unique value of the ionization parameter in the
HII region. This is because the pressure in the
stellar winds at the outer boundary of the mass-loss bubble determines
the equilibrium pressure in the HII region
plasma. Thus, Pw = Lmech /
4 Rw2 vw =
PHII = nHII kTHII,
where vw is the mean stellar wind velocity measured at
the radius of termination of the free-wind region
Rw. This free-wind boundary is visible in
Fig 2 as the boundary of the inner region where
the cross-shaped cooling artifacts in the free-wind resulting from the
finite wind injection region give way to the shocked hot turbulent gas
filling the rest of the bubble. In general we can take
Rw =
Rw2 vw =
PHII = nHII kTHII,
where vw is the mean stellar wind velocity measured at
the radius of termination of the free-wind region
Rw. This free-wind boundary is visible in
Fig 2 as the boundary of the inner region where
the cross-shaped cooling artifacts in the free-wind resulting from the
finite wind injection region give way to the shocked hot turbulent gas
filling the rest of the bubble. In general we can take
Rw =  R with
R with
 ~ 0.3. Thus:
~ 0.3. Thus:
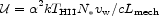 |
(21) |
Since the HII region temperature is always THII ~ 104K, then, for any central star cluster at a particular time in its evolution, the ionization parameter is determined solely by the instantaneous ratio of N* vw / Lmech. Thus, for coaeval clusters which are massive enough so that stochastic variations in these quantities are unimportant, the ionization parameter will be essentially independent of cluster mass and is only a function of cluster age. All the quantities needed to compute the ionization parameter, are given in the STARBURST99 output files.
Since the extended atmosphere of the exciting stars absorb a greater and
greater fraction of the ionising photons as the metallicity increases,
and at greater metallicity a greater fraction of the momentum flux in
the radiation field is converted to mechanical energy in the winds, the
ratio of N* vw /
Lmech
strongly decreases as the metallicity increases. The effect of this on
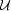 is shown in
Fig 3.
is shown in
Fig 3.
Dust Temperatures The determination of the dust temperature, or more properly the shape and the peak of the far-IR bump in starburst SEDs is not so straightforward as determining the ionization parameter. However, the general physics that drives the distribution of dust temperatures is readily understood.
We saw above how HII region in high pressure (or density) environments will stall at a smaller radius, according to the Oey & Clark theory [65, 66]. This means that the dust within the ionized gas of the HII regions will be hotter when the ISM pressure is high. At the outer boundary of the HII region we normally expect to find molecular clouds in approximate pressure equilibrium with the ionized gas. Therefore, the radiation field with energies below the Lyman Limit is absorbed by the gas and the dust in a rather thin photodissociation region (PDR) behind the ionization front which bounds these molecular clouds. At any point in the PDR, the local radiation field is determined only by the radiation field incident on the molecular cloud and by the optical depth up to that point. For a given grain size distribution and composition, the grain temperature distribution, and hence the far-IR re-emission function, is determined by the local radiation field. The global far-IR spectrum is the integral of the local far-IR spectra through the PDR. Hence the far-IR spectrum is determined only by the radiation field incident on the molecular cloud.
The result of this is that smaller HII regions, which are preferentially encountered in region of the ISM with higher pressure will be characterised by hotter far-IR dust emission spectra. Provided that the PDR remains thin in comparison with the radius of the HII region, the far-IR spectrum of the ensemble of HII regions remains a function only of the pressure. The abundance of the heavy elements can only make a difference when the changing abundance drives a changing grain size distribution, when the changing ratio of photon energy to mechanical energy produced by the central stars leads to a changing size distribution in the HII region population, or when the opacity of the grains falls so low that the spherical divergence of the radiation field through the PDR becomes important. This dependence of the far-IR spectrum on pressure is illustrated in Fig 4.
The invariance of the PAH features in these models is interesting. This occurs despite the fact that the abundance of changes by a factor of nearly 30, and the relative abundance of PAH molecules relative to silicaceous grains decreases strongly at low metallicity. The reason for this is that at the wavelength where they strongly absorb, the PAH molecules dominate the total dust and molecular opacity. They therefore convert a fixed fraction of the bolometric luminosity of the star to PAH emission features. In order to decrease the relative strength of the PAH features at low metallicity, we need to ensure that the molecular clouds become "leaky" to the incident radiation, which requires that the column density in the molecular clouds does not exceed ~ 3 × 1021 H atoms cm-2.