


3.3. The destruction of SN condensates by the reverse shock
To these destruction processes we add the destruction of SN-condensed dust grains by the reverse shock propagating through the SN ejecta. The reverse shock is caused by the interaction of the ejecta with the ambient medium. Figure 4 is a schematic reproduction of a similar figure in [62], depicting the interaction of the SN ejecta during the free expansion phase of its evolution with its surrounding medium. This medium could consist of either circumstellar material that was ejected by the progenitor star during the red giant phase of its evolution, or interstellar material. The SN ejecta acts like a piston driving a blast wave into the ambient medium. Immediately behind the blast wave is a region of shocked swept-up gas. When the pressure of this shocked gas exceeds that of the cooling piston, a reverse shock will be driven into the ejecta [52].
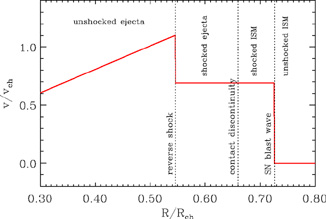 |
Figure 4. A schematic diagram (after Truelove & McKee [62]) depicting the interaction of the SN ejecta with its ambient surrounding. |
Dust formed in the ejecta will be subject to thermal sputtering by the
reverse shock. The fraction of dust destroyed is roughly given by the
ratio of the sputtering lifetime,
 sput, to the
expansion time (age), t, of
the ejecta. The grain lifetime is initially a strongly rising function
of gas temperature, reaching a plateau at about 106 K
[16].
Figure 5 depicts the velocity history of the
reverseshock as it traverses different layers of the ejecta, as a
function of
sput, to the
expansion time (age), t, of
the ejecta. The grain lifetime is initially a strongly rising function
of gas temperature, reaching a plateau at about 106 K
[16].
Figure 5 depicts the velocity history of the
reverseshock as it traverses different layers of the ejecta, as a
function of 
 Rr /
Rej, where Rr is the radius of the
reverse shock, and Rej is the outer radius of the
ejecta. The calculations were performed using the analytical expressions
of Truelove & McKee
[62]
for a SN explosion in a uniform medium. The initial velocity of the
reverse shock at
Rr /
Rej, where Rr is the radius of the
reverse shock, and Rej is the outer radius of the
ejecta. The calculations were performed using the analytical expressions
of Truelove & McKee
[62]
for a SN explosion in a uniform medium. The initial velocity of the
reverse shock at
 = 1 is zero, reaching a
maximum at
= 1 is zero, reaching a
maximum at  = 0, when it
reaches the origin of the explosion. No dust will be destroyed at
= 0, when it
reaches the origin of the explosion. No dust will be destroyed at
 = 1, since the gas
temperature so low that most gas molecules have kinetic energies well
below the sputtering threshold. Very little grain destruction is also
expected to take place at
= 1, since the gas
temperature so low that most gas molecules have kinetic energies well
below the sputtering threshold. Very little grain destruction is also
expected to take place at
 = 0 since in spite of
the high gas temperature, the gas density is very low and the sputtering
lifetime is longer than the expansion time of the ejecta. There is
therefore an optimal location 0
<
= 0 since in spite of
the high gas temperature, the gas density is very low and the sputtering
lifetime is longer than the expansion time of the ejecta. There is
therefore an optimal location 0
<  < 1, where the
shock velocity (gas temperature) and ejecta density are such that
< 1, where the
shock velocity (gas temperature) and ejecta density are such that
 sput / t
< 1, and grain destruction can take place.
sput / t
< 1, and grain destruction can take place.
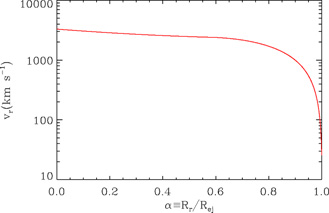 |
Figure 5. The velocity profile of the
reverse shock traversing the SN ejecta. The reverse shock originates at
|
The  -interval in which
grains are completely destroyed will depend on the size of the
newly-nucleated dust particles. Figure 6 depicts
the location in the ejecta in which dust is completely destroyed by the
reverse shock. The calculations were performed for dust particles with
radii of 0.1 and 0.01 µm embedded in a smooth, O-rich
ejecta. As expected, the smaller dust particles are destroyed over a
wider range of ejecta layers compared to the larger size particles. In
reality, SN ejecta are clumpy, and the SN dust is expected to reside
predominantly in the clumpy phases of the ejecta, as is suggested by the
detection of dust in the fast moving knots of the remnant of Cas A
[45,
3].
The reverse shock slows down below the threshold for complete grain
destruction as it traverses these density enhancements in the
ejecta. Consequently, dust in the clumpy ejecta may only be shattered
instead of being completely destroyed by sputtering. The total amount of
grain processing in the SN ejecta is however still highly uncertain.
An independent investigation into the effect of reverse shocks from the
H-envelope, the presupernova wind, and the ISM on the formation of dust,
the amount of grain processing, and the implantation of isotopic
anomalies in SN ejecta was carried out by Deneault, Clayton, & Heger
[9].
-interval in which
grains are completely destroyed will depend on the size of the
newly-nucleated dust particles. Figure 6 depicts
the location in the ejecta in which dust is completely destroyed by the
reverse shock. The calculations were performed for dust particles with
radii of 0.1 and 0.01 µm embedded in a smooth, O-rich
ejecta. As expected, the smaller dust particles are destroyed over a
wider range of ejecta layers compared to the larger size particles. In
reality, SN ejecta are clumpy, and the SN dust is expected to reside
predominantly in the clumpy phases of the ejecta, as is suggested by the
detection of dust in the fast moving knots of the remnant of Cas A
[45,
3].
The reverse shock slows down below the threshold for complete grain
destruction as it traverses these density enhancements in the
ejecta. Consequently, dust in the clumpy ejecta may only be shattered
instead of being completely destroyed by sputtering. The total amount of
grain processing in the SN ejecta is however still highly uncertain.
An independent investigation into the effect of reverse shocks from the
H-envelope, the presupernova wind, and the ISM on the formation of dust,
the amount of grain processing, and the implantation of isotopic
anomalies in SN ejecta was carried out by Deneault, Clayton, & Heger
[9].