Copyright © 2000 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 2000. 38:
667-715 Copyright © 2000 by Annual Reviews. All rights reserved |
5.6. Clustering of high-redshift galaxies
Until relatively recently, evolution of the spatial two-point
correlation function
 has typically
been modeled as a simple power-law evolution in redshift
has typically
been modeled as a simple power-law evolution in redshift
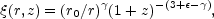 |
(3) |
where r and r0 are expressed in comoving
coordinates (e.g.
[Groth & Peebles
1977]).
For  = 0,
the formula above corresponds to stable clustering (fixed in
proper coordinates), while for
= 0,
the formula above corresponds to stable clustering (fixed in
proper coordinates), while for
 =
=
 - 3 it
corresponds to a clustering pattern that simply expands with
the background cosmology. Although these two cases may bound the
problem at relatively low redshift, the situation becomes
much more complex as galaxies surveys probe to high redshifts.
In particular, the complex merging and fading histories of
galaxies make it unlikely that such a simple formula could
hold, and the differences in sample selection at high and
low-z make it unclear whether the analysis is comparing
the same physical entities.
In practice it is likely that galaxies are biased
tracers of the underlying dark-matter distribution, with a bias
factor b that is non-linear, scale-dependent,
type-dependent, and stochastic
[Magliocchetti et
al. 1999,
Dekel & Lahav
1999].
- 3 it
corresponds to a clustering pattern that simply expands with
the background cosmology. Although these two cases may bound the
problem at relatively low redshift, the situation becomes
much more complex as galaxies surveys probe to high redshifts.
In particular, the complex merging and fading histories of
galaxies make it unlikely that such a simple formula could
hold, and the differences in sample selection at high and
low-z make it unclear whether the analysis is comparing
the same physical entities.
In practice it is likely that galaxies are biased
tracers of the underlying dark-matter distribution, with a bias
factor b that is non-linear, scale-dependent,
type-dependent, and stochastic
[Magliocchetti et
al. 1999,
Dekel & Lahav
1999].
In hierarchical models, the correlation function
 (r)
of halos on linear scales is given by the statistics of peaks in a
Gaussian random field
[Bardeen et
al. 1986].
Peaks at a higher density threshold
(r)
of halos on linear scales is given by the statistics of peaks in a
Gaussian random field
[Bardeen et
al. 1986].
Peaks at a higher density threshold

 /
/
 have a higher
correlation amplitude, and their bias
factor b, relative to the overall mass distribution is
completely specified by the number-density of peaks (e.g
[Mao & Mo 1998]).
have a higher
correlation amplitude, and their bias
factor b, relative to the overall mass distribution is
completely specified by the number-density of peaks (e.g
[Mao & Mo 1998]).
The comparison of the clustering of high-redshift galaxies in the HDF and in ground-based surveys provides a strong test of whether there is a one-to-one correspondence between galaxies and peaks in the underlying density field. The bias factor observed in Lyman-break samples [Steidel et al. 1998, Adelberger et al. 1998, Giavalisco et al. 1998] is in remarkable agreement with the expectations from such a one-to-one correspondence. As the luminosity of Lyman-break galaxies decreases, the number density increases, and the clustering amplitude decreases [Giavalisco et al. 2000]. These trends are all in agreement with a scenario in which lower-luminosity Lyman-break galaxies inhabit lower-mass halos. Thus, at redshifts z ~ 3, the connection between galaxies and dark matter halos may in fact be quite simple and in good agreement with theoretical expectations.
The picture becomes less clear for the samples described in
Section 4.12.
In particular, the interpretation
of the apparent evolution in the correlation length r0
or the bias factor b from the
[Magliocchetti
& Maddox 1999]
and
[Arnouts et
al. 1999]
studies involves a sophisticated treatment of the merging of galaxies and
galaxy halos over cosmic time. Fairly detailed attempts at this have
been made using either semi-analytic models
[Baugh et al. 1999,
Kauffmann et
al. 1999]
or more generic arguments (e.g.
[Matarrese et
al. 1997,
Moscardini et
al. 1998,
Magliocchetti et
al. 1999],
following on earlier work by
[Mo & Fukugita
1996],
[Mo & White 1996],
[Jain1997],
[Ogawa et al. 1997]
and others). These studies all assume that
galaxy mass is directly related to halo mass, which may not be true in
reality at lower z, but which is an assumption worth testing. A
generic prediction of the models is that the effective bias factor (the
value of b averaged over the mass function) should increase with
increasing redshift. The correlation length r0 is
relatively independent of
redshift (to within factor of ~ 3), in contrast to the factor of
~ 10 decline from z = 0 to z = 4 predicted for
non-evolving bias. The results shown by
[Arnouts et
al. 1999]
are qualitatively consistent
with this behavior. However, it
is worth re-emphasizing that the HDF is a very small field.
The standard definition for the bias factor b is the ratio of
the root mean square density fluctuations of galaxies relative to mass
on a scale of
8h-1 Mpc. Fluctuations on this angular scale
clearly have not been measured in the HDF, and the interpretation
rests on (a) the assumption of a powerlaw index
 = 1.8 for
the angular correlation function (which is not in fact predicted
by the models)
[Moscardini et
al. 1998],
and (b) the fit
to the integral constraint. Clearly much larger areas are needed
before secure results can be obtained.
= 1.8 for
the angular correlation function (which is not in fact predicted
by the models)
[Moscardini et
al. 1998],
and (b) the fit
to the integral constraint. Clearly much larger areas are needed
before secure results can be obtained.
[Roukema &
Valls-Gabaud 1997] and
[Roukema et
al. 1999]
point out that much
of the measured clustering signal in the HDF comes from scales
25 - 250 kpc, which is within the size of a typical
L* galaxy
halo at z = 0. The connection of the observed correlation function
to hierarchical models thus depends quite strongly on
what happens when multiple galaxies inhabit the same halo.
Do they co-exist for a long time (e.g. as in present-day galaxy
groups and clusters), or rapidly merge together to form a larger
galaxy (in which case one should consider a "halo exclusion
radius" in modeling the correlation function)? As the
halo exclusion radius increases, the predicted correlation
amplitude on scales of 5" decreases relative to the standard
cosmological predictions. The slope of
 (
( ) also differs from
) also differs from
 = 1.8 for
= 1.8 for

 20".
[Roukema et
al. 1999]
find that the HDF data for
1.5 < zphot < 2.5
are best fit with stable clustering, a halo-exclusion radius
of rhalo = 200h-1 kpc, and a
low-density universe.
20".
[Roukema et
al. 1999]
find that the HDF data for
1.5 < zphot < 2.5
are best fit with stable clustering, a halo-exclusion radius
of rhalo = 200h-1 kpc, and a
low-density universe.