2.3. Concentration

For many years astronomers have had an interest in how centrally concentrated a galaxy's stellar distribution is (e.g., Morgan 1958, 1959, 1962; Fraser 1972; de Vaucouleurs 1977). Sérsic (1968) used de Vaucouleurs (1956) somewhat subjective size ratio between the main region of the galaxy and the apparent maximum dimension of the galaxy as a measure of concentration.

Trujillo, Graham & Caon (2001c) defined a useful, objective expression for concentration, such that, in pixelated form

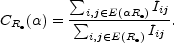
(20)

Here, E(R_e) means the isophote which encloses half of the total light, and E( R_e) is the isophote at a radius (0 < < 1) times R_e. This is a flux ratio. For a Sérsic profile which extends to infinity,

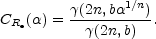
(21)

This expression is a monotonically increasing function of n, and for = 1/3 it's values are shown in Figure (3). An often unrealized point is that if every elliptical galaxy had an R^1/4 profile then they would all have exactly the same degree of concentration. Observational errors aside, it is only because elliptical galaxy light-profiles deviate from the R^1/4 model that a range of concentrations exist. This is true for all objective concentration indices in use today.

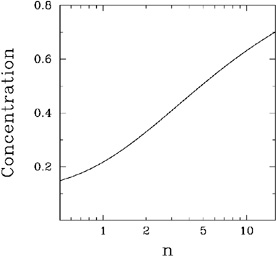Figure 3. The central concentration CRe(1/3), as defined by Trujillo et al. (2001c), is a monotonically increasing function of the Sérsic index n.

It should be noted that astronomers don't actually know where the edges of elliptical galaxies occur; their light-profiles appear to peeter-out into the background noise of the sky. Due to the presence of faint, high-redshift galaxies and scattered light, it is not possible to determine the sky-background to an infinite degree of accuracy. From an analysis of such sky-background noise sources, Dalcanton & Bernstein (2000, see also Capaccioli & de Vaucouleurs 1983) determined the limiting surface brightness threshold to be ~ 29.5 B-mag arcsec^-2 and µ ~ 29 R-mag arcsec^-2. Such depths are practically never achieved and shallow exposures often fail to include a significant fraction of an elliptical galaxy's light. One would therefore like to know how the concentration index may vary when different galaxy radial extents are sampled but no effort is made to account for the missed galaxy flux. The resultant impact on C_Re and other popular concentration indices is addressed in Graham, Trujillo, & Caon (2001).

It was actually, in part, because of the unstable nature of the popular concentration indices that Trujillo et al. (2001c) introduced the notably more stable index given in Equations (20) and (21). The other reason was because the concentration index C() = _{i,j E()} I_ij / _{i,j 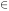E(1)} I_ij, where E() denotes some inner radius which is (0 < < 1) times the outermost radius which has been normalized to 1 (Okamura, Kodaira, & Watanabe 1984; Doi, Fukugita, & Okamura 1993; Abraham et al. 1994), should tend to 1 for practically every profile that is sampled to a large enough radius. It is only because of measurement errors, undersampling, or the presence of truncated profiles such as the exponential disks in spiral galaxies, that this index deviates from a value of 1.