2.4. Profile slopes

Given HST's ability to resolve the inner light-profiles of nearby galaxies, the slope of a galaxy's nuclear (the inner few hundred parsec) stellar distribution has become a quantity of interest. Defining ⁵

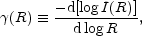
(22)

Rest et al. (2001, their Equation 8) used this to measure the nuclear slopes of `core' and `power-law' galaxies. From Equation (1) one can obtain

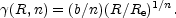
(23)

This is approximately 2(R / R_e)^1/n (see section 2.1). Thus, at constant (R / R_e), is a monotonically increasing function of the Sérsic index n (Graham et al. 2003b).

It turns out Equation (23) is appropriate for the so-called `power-law' galaxies which are now known to possess Sérsic profiles down to their resolution limit (Trujillo et al. 2004) and would be better referred to as `Sérsic' galaxies as they do not have power-law profiles. A modification is however required for the luminous `core galaxies', and is described in Section 2.7.

Another logarithmic slope of interest is that used by Gunn & Oke (1975) and Hoessel (1980), and is defined as

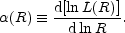
(24)

From Equation (2) one has

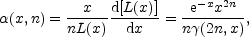
(25)

where, as before, x = b(R / R_e)^1/n (Graham et al. 1996, their equation 8).

Figures (4) and (5) show how (R) and (R) vary with normalised radius R / R_e for a range of different profile shapes n.

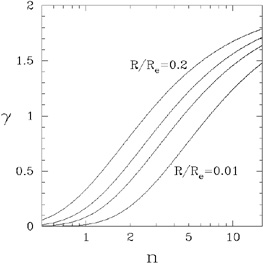Figure 4. The slope of the Sérsic profile (Equation 23) is shown as a function of profile shape n for R / Re = 0.01, 0.05, 0.1, and 0.2.

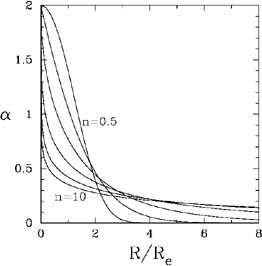Figure 5. The slope (Equation 25) is shown as a function of normalised radius R / Re for n = 0.5, 1, 2, 4, 7, and 10.

⁵ This should not be confused with the incomplete gamma function seen in Equation (3). Back.