


In order to convert the luminosity function to a mass function, we require the mass-to-light ratio of the stellar populations. This will in general be a function of galaxy type, age and metallicity. We determine the mean mass-to-light ratio of ellipticals and assume that this may also be applied to the bulge component of S0 and spiral galaxies. We then determine the mass-to-light ratio of discs, irregular galaxies and dwarf elliptical galaxies. These mass-to-light ratios are then combined using bulge-to-disc ratios, µB, using the measurements of [Kent 1985]. The results are presented, along with the gas properties of galaxies that we derive in the next section, in table 2.
| µB | M/LB | mHI / LB | mH2 / mHI | |
| E | 1 | 6.8-7.5 | ~ 0.01 | ~ 1 |
| S0+S0/a | 0.64 | 4.8-5.4 | 0.11-0.33 | 1.3-6.7 |
| Sa+Sab | 0.33-0.40 | 3.1-3.6 | 0.078-0.32 | 1.5-5.8 |
| Sb+Sbc | 0.16-0.25 | 2.1-2.6 | 0.24-0.46 | 2.0-4.2 |
| Sc+Scd | 0.06-0.09 | 1.6-2.1 | 0.46-0.65 | 1.1-1.8 |
| Sd+Sdm+Sm | ~ 0 | 1.6-2.1 | 0.62-0.70 | 0.70-1.3 |
| Irr+dIrr | ~ 0 | 0.9-1.2 | 0.55-0.99 | 0.30-0.58 |
| dE | - | 1.7-4.9 | ~ 0 | - |
(i) Ellipticals and bulges
Two methods were employed here. The first uses
stellar population synthesis models to convert an age, metallicity and
colour into a B-band mass-to-light ratio M /
LB. We use the models of
[Bruzual
& Charlot 2003]
with an initial stellar mass function
(IMF) (M)
7, taken from
[Kroupa
2001]:
(M)
7, taken from
[Kroupa
2001]:
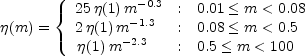 |
(1) |
where m is in units of solar masses
M .
The results are very sensitive to the IMF, since
arbitrarily many low-mass stars can be included with no change to the
measured colour, metallicity or age of a galaxy.
.
The results are very sensitive to the IMF, since
arbitrarily many low-mass stars can be included with no change to the
measured colour, metallicity or age of a galaxy.
This IMF has been empirically determined from deep observations of local field stars and of young star clusters. It is denoted the `universal IMF' since it appears to be the same across the enormous range of scale, environment and epoch in which it has been determined [Kroupa 2001]. This IMF is also attractive in that it is the end result of star formation that exhibits a Salpeter IMF whilst in progress ([Kroupa & Weidner 2003])
Using the stellar population models of
[Bruzual
& Charlot 2003],
adopting the IMF above, and assuming a mean age and
metallicity for ellipticals of
tE  12
± 2 Gyr and Z = 2
Z
12
± 2 Gyr and Z = 2
Z 8 respectively, we obtain
M / LB = 9.81 - 11.05.
8 respectively, we obtain
M / LB = 9.81 - 11.05.
We may also obtain the mass to light ratio of ellipticals from dynamics. While there is significant evidence for dark matter in ellipticals, interior to the majority of the stellar light the dark matter component is small ([van der Marel 1991] and [Kronawitter et al. 2000]) so the stellar velocities (as measured from their relative Doppler shifts) may be used to calculate the total gravity produced by masses of the stars.
A recent study of 21 elliptical galaxies by [Kronawitter et al. 2000] gives M / LB = 6.78 - 7.54 which is a factor ~ 0.7 of the stellar population value. This is very surprising since the presence of dark matter should tend to make the stellar populations value smaller than the dynamical estimate rather than the other way round. We favour the dynamical estimate because modelling stellar populations is extremely difficult and errors of the order 2 are not uncommon [Charlot et al. 1996]. Perhaps more importantly, the `universal' IMF of [Kroupa (2001)] has not been explicitly verified for elliptical galaxies and so may not be the correct one to use [Jorgensen 1997]. Given these uncertainties, we adopt the dynamical values of M / LB in this work.
(ii) The mass-to-light ratio of discs
Following
[Fukugita
et al. 1998]
we compile a mean mass to light
ratio for discs from three independent methods. The first is from
measurements of the column density of stars in the solar
neighbourhood,
 *
= 27 - 40
M
*
= 27 - 40
M pc-2
([Gould
et al. 1996] and
[Kuijken
& Gilmore 1989]).
Combining this with the local luminosity surface density,
pc-2
([Gould
et al. 1996] and
[Kuijken
& Gilmore 1989]).
Combining this with the local luminosity surface density,
 LB
LB
 18
M
18
M pc-2
[Bahcall
& Soneira 1980]
gives M / LB = 1.5 - 2.2.
The second method uses the stellar population synthesis models of
[Tinsley
1981] and
[Portinari
et al. 2004].
These are on a firmer footing than for the elliptical galaxies since the
IMF has been explicitly measured for spiral galaxies
[Kroupa
2001].
These give M / LB = 1.1 - 1.9 using the IMF
given in equation 1.
The third method uses a dynamical mass estimate for the stars
([Salucci
& Persic 1999]).
This gives M / LB = 1.11.
pc-2
[Bahcall
& Soneira 1980]
gives M / LB = 1.5 - 2.2.
The second method uses the stellar population synthesis models of
[Tinsley
1981] and
[Portinari
et al. 2004].
These are on a firmer footing than for the elliptical galaxies since the
IMF has been explicitly measured for spiral galaxies
[Kroupa
2001].
These give M / LB = 1.1 - 1.9 using the IMF
given in equation 1.
The third method uses a dynamical mass estimate for the stars
([Salucci
& Persic 1999]).
This gives M / LB = 1.11.
The mean of all of these values gives M / LB = 1.24 - 1.7. We adopt this value here. This value was then corrected for internal extinction in the galaxies, using the corrections of [Tully & Fouque 1985] and a field sample inclination distribution equivalent to that seen in the Ursa Major Cluster [Tully et al. 1996].
(iii) The mass to light ratio of dwarfs and irregulars
The mass-to-light ratios for the irregulars (and dwarf irregulars) may be adapted from the above value for discs corrected for their younger age and consequent bluer colour [Fukugita et al. 1998]: M / LB = 0.9 - 1.24.
Recent observations of the Ursa Minor local group dwarf elliptical (dE) 9 galaxy by [Wyse et al. 2002] suggest that dE stellar populations are very similar to the Milky Way globular clusters. As such, we use the dynamical mass-to-light ratio of Galactic globular clusters ([Pryor & Meylan 1993]) for dE galaxies: M / LB = 1.7 - 4.9.
We find excellent agreement between our derived stellar mass function
and that of
[Panter
et al. 2004]
(see the black dotted line in figure 2).
They also use the SDSS data, but derived stellar masses
from star formation histories constrained by the spectra of
the galaxies. This gives some weight to the validity of our method of
classifying galaxies by Hubble type and then determining masses.
Our data gives
 *
= 0.0028 ± 0.0003, whereas Panter et al. find
*
= 0.0028 ± 0.0003, whereas Panter et al. find
 *
= 0.0034 ± 0.0001.
*
= 0.0034 ± 0.0001.
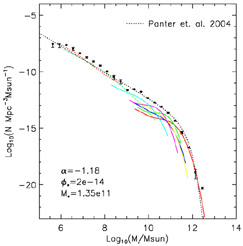 |
Figure 2. The field galaxy stellar mass function split by galaxy Hubble type. The data points are for all galaxies, while the lines show spine fits by Hubble Type. The lines have the same meaning as in figure 1. Bright (massive galaxies) lie to the right of this plot, while faint galaxies lie to the left. Overlaid are parameters for a Schechter fit to the total mass function. |
7 The stellar IMF is defined such that
 (M) is
the number of stars in the interval M to M + dM.
M
(M) is
the number of stars in the interval M to M + dM.
M =
1.989 × 1030 kg is the mass of the sun.
Back.
=
1.989 × 1030 kg is the mass of the sun.
Back.
8 The metallicity, Z is the ratio of the total mass in heavy elements, Mh, to the total baryonic mass [Binney & Merrifield 1998]. Back.
9 Ursa Minor or UMi is usually labelled as a dwarf spheroidal galaxy (dSph) which is an alternate name for a dwarf elliptical galaxy. Back.