


The gas mass function of local galaxies is presented in figure 3.
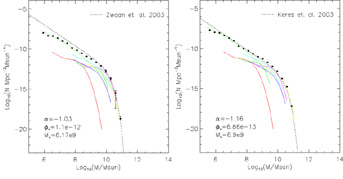 |
Figure 3. The field galaxy HI (left) and H2 (right) gas mass functions split by galaxy Hubble Type. The data points are for all galaxies, while the lines show spine fits by Hubble type. The lines are as in figure 1. Overlaid are parameters for a Schechter fit to the total mass function. |
A large sample of HI (atomic) gas measurements of nearby galaxies was compiled recently as part of the Australian HIPASS survey, using the Parkes radio telescope. Measurements of the 1000 brightest galaxies in this sample were recently published ([Koribalski et al. 2004]).
In order to measure the total amount of gas in galaxies in the Universe, we need to determine how much gas the galaxies contain per unit optical luminosity. We can then get the gas mass function from the luminosity function. We computed the atomic gas mass per unit luminosity for each Hubble Type as follows. We compiled a sample of galaxies with velocities between 2000 and 3000 km/s that were observed at optical wavelengths and also in HI in the HIPASS survey. For each Hubble Type, we used this sample to determine the ratio between the atomic gas mass and the optical luminosity. These numbers are given in table 2. The wide ranges reflect the conservative error estimates that we are forced to use because of the intrinsic scatter in the ratio for galaxies of a given Hubble Type and because the errors are systematic.
The HI mass function that we derived is very similar to the one derived
by HIPASS
(Zwaan et al. 2003)
at the high-mass end, but falls significantly below theirs at the
low-mass end. This difference can be attributed to the difference in
sample selection and scaling - the HIPASS sample is selected by HI mass
but ours is selected and scaled by optical luminosity. They therefore
include many systems that we do not, as well as include gas that in the
outer parts of the galaxies that is not included in our analysis -
a galaxy that we think has mass M of atomic gas may really have
2M, so our points should be shifted towards the left if we
wish to include all the atomic gas in the Universe. Both of these
effects could be more important at low masses - the highest mass
HI galaxies will invariably be in optical surveys, and all scaling
relations were derived using the properties of these galaxies..
This difference also accounts in our different values of
 HI:
HIPASS finds
HI:
HIPASS finds
 HI = (4.1
± 0.6) × 10-4 whereas we get
HI = (4.1
± 0.6) × 10-4 whereas we get
 HI = (2.9
± 0.6) × 10-4.
HI = (2.9
± 0.6) × 10-4.
Similarly, we determine the relationship between galaxy Hubble Type and
molecular gas mass using the data of
[Young
et al. 1995].
The results are also presented in table 2.
This survey measures CO line luminosities, which are converted to gas masses
using the empirical formula of
[Young
& Scoville 1991]:
MH2 = 12000 SCO
D2
M ,
where SCO is the CO flux in Jy km/s and D is
the distance to the galaxy in Mpc.
,
where SCO is the CO flux in Jy km/s and D is
the distance to the galaxy in Mpc.
We find a very similar molecular gas mass function to that of [Keres et al. (2003)], who presented this function for a far-infrared (FIR)-selected sample, also derived from the [Young et al. (1995)] sample. This is consistent with the idea that most of the molecular gas in the Universe is in normal galaxies, which are the same objects as the FIR sources.