


Clusters of galaxies have proved a popular environment for determining the LF. This is because the distances to the galaxies there are known (at least in a statistical sense) so that the LF can be determined by photometry alone and spectroscopic redshifts are not needed. This in turn means that the LF can be measured down to very faint limits.
But there is a price to be paid for the cosmologist. Cluster galaxies are in dense environments where the crossing time plus age is less than or comparable to the Hubble time. These galaxies have therefore had their properties shaped by cluster-related processes e.g. ram-pressure stripping of gas from the galaxies. Measurements of the galaxy LF in clusters might then tell us more about these cluster-related processes than about cosmological parameters like the shape of the power spectrum on small mass scales. This is particularly true of very dense environments like the centers of rich clusters with large fractions of elliptical galaxies. It is less true of diffuse spiral-rich environments and the outer parts of clusters.
In Figure 1, for a sample of clusters with LF determinations, I present the velociy dispersion (an indication of the mass of the cluster) as a function of the cluster redshift z. Also shown on this figure are lines corresponding to 200 kpc = 10 arcmin - this is where a rich cluster core roughly fits into a single 2K CCD frame on a 2 to 4 meter telescope - and corresponding to where a typical dSph galaxy with R = 24 has a scale-length (as inferred from the Binggeli plot) of 1 arcsec - to the right of this line, most faint cluster galaxies detected have intrinsic scale-lengths smaller than the seeing and so cannot be readily discriminated from background galaxies on morphological grounds.
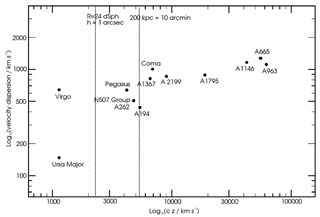 |
Figure 1. The velocity dispersions and redshifts for some clusters with recent LF determinations |
The techniques used to determine the LF in a particular cluster are determined by its position on Figure 1. In simplest terms, clusters are either on the left of the dashed lines (hereafter I call these "nearby clusters") or between or to the right of the dashed lines (I call these "distant clusters").
Most early work in this subject that reached absolute magnitudes faint enough to probe dwarf galaxies (those in sequence (4) of the Binggeli diagram) were photographic measurements of nearby clusters e.g. Virgo [29] and Fornax [10]. Clusters significantly more distant than Coma (see e.g. ref. 35 for a large photographic survey of Coma) could not be studied in this way because (i) photographic plates were not sensitive enough to probe the bulk of the dwarf population, and (ii) cluster members could not be readily distinguished from background/foreground galaxies.
However, the advent of 2K CCDs on 2 - 4 m telescopes allowed very precise statistical determinations of field galaxy counts down to very faint magnitudes (e.g. refs. 43 and 17). Background/foreground contamination in cluster fields could then be estimated and corrected for down to R = 25, and the LFs of several rich clusters out to z = 0.2 were measured. The main limitation of these studies was that the errors at the faintest magnitudes were quite large because of uncertainty in the field-to-field variance of the background. However, large samples of clusters could be studied, and these errors reduced when combining samples of similar clusters. In Section 5, some results of this type will be presented and discussed.
These 2K CCDs are not well suited to studies of nearby clusters, although individual dwarfs can easily be identified and no background subtraction is needed. This is because the CCDs are small and each exposure can only cover a negligible fraction of the cluster core (we are to the left of the 200 kpc = 10 arcmin line in Figure 1). Counting statistics are then crippling - a typical 2K CCD field in the center of the Virgo Cluster will have no or at most 1 or 2 dwarfs brighter than R = 22.
More recently, 8K and larger CCDs have become available on 4 m telescopes (e.g. the UH 8K mosaic on the 3.6 m CFHT [23]). Large samples of galaxies in nearby clusters can now be obtained and the LFs measured accurately down to very faint magnitudes. Because no background subtraction is required, the only errors at faint magnitudes come from counting statistics - the errors are consequently much smaller than the errors at the faint end for the distant clusters, at least for reasonably dense nearby clusters like Virgo and Fornax. An alternative approach has been employed by Phillipps et al. [27] who use sensitive median-stacked UK Schmidt plates [32] to measure the Virgo cluster LF down to MR ~ - 11.5 (see the paper by Jones et al. in these proceedings - this was one of the most significant new results at this meeting). A project in collaboration with B. Tully (University of Hawaii) has been undertaken to measure the Ursa Major LF but this cluster is sufficiently diffuse that counting statistics are still a significant problem.