3. PHYSICS OF REIONIZATION

Given the observational constraints discussed in the previous Section, it is important to develop models which can be reconciled with every data set. However, such a task is not straightforward simply because of the complexities in the physical processes involved. It is not that there is some unknown physics involved - we believe that we can write down every relevant equation - the difficulty lies in solving them in full generality. This is quite a common obstacle in most aspects of large scale structure formation, but let us concentrate on reionization for the moment.

A crucial issue about reionization is that this process is tightly coupled to the properties and evolution of star-forming galaxies and QSOs. Hence, the first requirement that any reionization model should fulfill is that it should be able to reproduce the available constraints concerning the luminous sources. Though there has been a tremendous progress in our understanding of formation of galaxies and stars at low redshifts, very little is known about the high redshift galaxies, particularly those belonging to the first generation. There are strong indications, both from numerical simulations and analytical arguments, that the first generation stars were metal-free, and hence massive, with a very different kind of spectrum than the stars we observe today [135]; they are known as the PopIII stars. Along similar lines, whereas a relatively solid consensus has been reached on the luminosity function, spectra and evolutionary properties of intermediate redshift QSOs, some debate remains on the presence of yet undetected low-luminosity QSOs powered by intermediate mass black holes at high redshift [136]. Even after modelling the ionizing sources to a reasonable degree of accuracy, predicting the joint reionization and star formation histories self-consistently is not an easy task as (i) we still do not have a clear idea on how the photons "escape" from the host galaxy to the surrounding IGM, and (ii) mechanical and radiative feedback processes can alter the hierarchical structure formation sequence of the underlying dark matter distribution as far as baryonic matter is concerned.

A different approach to studying reionization would be to parametrize the sources by various adjustable parameters (like efficiency of star formation, fraction of photons which can escape to the IGM, etc) and then calculate the evolution of global ionization and thermal properties of the IGM. Though it is possible to obtain a good qualitative picture of reionization through this approach, it is difficult to obtain the details, particularly those of the pre-overlap phase, through such simple analyses. For example, many details of the reionization process can be dealt only in an approximate manner (the shape of ionized region around sources and their overlapping, just to mention a few) and in terms of global averages (such as the filling factor and the clumping factor of ionized regions). We shall discuss this in more detail later in this Section.

It is thus clear that the complexities within the physics of reionization prohibit us from constructing detailed analytical models. The other option is to solve the relevant equations numerically and follow the ionization history. However, one should realize that in order to exploit the full power of the observational data available to constrain models, one must be able to connect widely differing spatial and temporal scales. In fact, it is necessary, at the same time, to resolve the IGM inhomogeneities (sub-kpc physical scales), follow the formation of the very first objects in which stars form (kpc), the radiative transfer of their ionizing radiation and the transport of their metals (tens of kpc), the build up of various radiation backgrounds (Mpc), and the effects of QSOs and sizes of the ionized regions (tens of Mpc). Thus, a proper modelling of the relevant physics on these scales, which would enable a direct and simultaneous comparison with all the available data set mentioned above, would require numerical simulations with a dynamical range of more than five orders of magnitude, which is far cry from the reach of our current computational technology. To overcome the problem, simulations have typically concentrated on trying to explain one (or few, in the best cases) of the observational constraints. It is therefore difficult from these studies to understand the extent to which their conclusions do not conflict with a different set of experiments other than the one they are considering.

However, one must realise that in spite of these difficulties in modelling reionization there have been great progresses in recent years, both analytically and through numerical simulations, in different aspects of the process. This Section will be devoted to the successes we have achieved towards understanding reionization.

3.1. Analytical approaches

As far as the analytical studies are concerned, there are two broad approaches in modelling, namely, (i) the evolution of ionized regions of individual ionizing sources and (ii) statistical approaches in computing the globally averaged properties and fluctuations.

The standard picture of reionization by discrete sources of radiation is characterized by the expansion and overlap of the individual ionized regions. In this paradigm, it is important to understand how the ionized regions evolve for different types of ionizing sources.

The most common sources studied are the ones with UV photons, i.e., photons with energies larger than 13.6 eV but within few tens of eV. These photons ionize and heat up the IGM through photoionizing neutral hydrogen (and possibly helium). Because of (i) a large value of the photoionization cross section around 13.6 eV, (ii) rapid increase of the number of absorbers (Ly "clouds") with lookback time and (iii) severe attenuation of sources at higher redshifts, the mean free path of photons at 13.6 eV becomes so small beyond a redshift of 2 that the radiation is largely "local". For example, the mean free path at 13.6 eV is typically 30 proper Mpc at z 3, which is much smaller than the horizon size. In this approximation, the background intensity depends only on the instantaneous value of the emissivity (and not its history) because all the photons are absorbed shortly after being emitted (unless the sources evolve synchronously over a timescale much shorter than the Hubble time).

When an isolated source of ionizing radiation, say a star or a QSO, turns on, the ionized volume initially grows in size at a rate determined by the emission of UV photons. The boundary of this volume is characterised by an ionization front which separates the ionized and neutral regions and propagates into the neutral gas. Most photons travel freely in the ionized bubble and are absorbed in a transition layer. Across the front the ionization fraction changes sharply on a distance of the order of the mean free path of an ionizing photon (which is much smaller than the horizon scale). The evolution of an expanding ionized region is governed by the equation [57, 137]

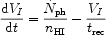(5)

where V_I is the comoving volume of the ionized region, 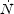_ph is the number of ionizing photons emitted by the central source per unit time, n_HI is the mean comoving density of neutral hydrogen and t_rec is the recombination timescale of neutral hydrogen given by

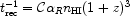(6)

In the above relation _R denotes the recombination rate ionized hydrogen and free electrons and is the clumping factor which takes into account the enhancement in the number of recombinations due to density inhomogeneities. It is clear from equation (5) that the growth of the ionized bubble is slowed down by recombinations in the highly inhomogeneous IGM. In the (over)simplified case of both 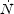_ph and t_rec not evolving with time, the evolution equation can be solved exactly to obtain

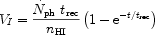(7)

While the volume of the ionized region depends on the luminosity of the central source, the time it takes to produce an ionization-bounded region is only a function of t_rec. It is clear that the ionized volume will approach its Strömgren radius after a few recombination timescales. Thus, when the recombination timescale is similar to or larger than the Hubble time (which is usually the case at lower redshifts, but depends crucially on the value of the clumping factor), the ionized region will never reach the Strömgren radius. The solution of the equation is more complicated in reality where the sources evolve, but the qualitative feature remains the same. After the bubbles have grown sufficiently, these individual bubbles start overlapping with each other eventually complete the reionization process.

As far as the hydrogen reionization is concerned, the evolution of the ionization front for stars and QSOs are qualitatively similar. The only difference is that the QSOs are much more luminous than stellar sources and hence the ionization front propagates much faster for QSOs. In the case of doubly-ionized helium, however, the propagation of ionization fronts for the two types of sources differ drastically. ⁴ Since normal stars hardly produce any photons above 54.4 eV, the propagation of the doubly-ionized helium ionization front is negligible; in contrast the QSOs have a stiff spectrum and one can show that the doubly-ionized helium front not only propagates quite fast into the medium, but closely follows the ionized hydrogen one. The analyses actually predict that the ionization of hydrogen and double-ionization of helium would be nearly simultaneous if QSOs were the dominant source of reionization, which cannot be the case for normal stellar population. Also note that the early metal-free massive PopIII stars too have a hard spectrum, and in their case the reionization of hydrogen and singly-ionized helium is simultaneous, similar to QSOs. This could provide an indirect way of identifying the sources of reionization from future observations.

If the sources of radiation produce photons of much higher energies, say in the X-ray band, the nature of the ionization front changes considerably. The most common example of such sources is the early population of accreting black holes, or miniquasars [138, 139]. These sources are expected to produce photons in the X-ray bands. The photons which are most relevant for this discussion would be those with energies below 2 keV, as photons with higher energies have mean free path similar to the horizon scale and thus would rarely be absorbed.

Since the absorption cross section of neutral hydrogen varies with frequency approximately as ^-3, the mean free path for photons with high energies would be very large. A simple calculation will show that for photons with energies above 100-200 eV, the mean free path would be larger than the typical separation between collapsed structures [140] (the details would depend upon the redshift and exact description of collapsed haloes). These photons would not be associated with any particular source at the moment when they are absorbed, and thus would ionize the IGM in a more homogeneous manner (as opposed to the overlapping bubble picture for UV sources). However, one should also note that the number of photons produced in the X-ray bands is usually not adequate for fully ionizing the IGM. Hence these hard photons can only partially ionize the IGM through repeated secondary ionizations. Basically, the photoelectron produced by the primary ionization would be very energetic (~ 1 keV) and could thus produce quite a few (~ 10) secondary electrons via collisional ionization. This may not be a very effective way of producing free electrons (when compared to the UV background), but is an efficient way of heating up the medium. This very population of hard photons deposits a fraction of its energy and can heat up the IGM to ~ 100 - 1000 K [141] before reionization - a process sometimes known as preheating.

In case of reionization through more exotic sources like decaying particles, the nature of ionized volumes would be completely different. The production of ionizing photons (or electrons) in this case is not related to any collapsed structure - rather it occurs throughout the space in an homogeneous manner. In such case, one expects only limited patchiness in the distribution of the background radiation or ionized fraction.

We have discussed various different ways in which the ionized regions could evolve depending on the nature of the ionizing sources. The next step would be to take into account the global distribution of the sources and ionized volumes and thus construct the global picture of reionization, which we shall study in the next subsection.

3.1.2. Statistical approaches

The most straightforward statistical quantity which is studied in reionization is the volume filling factor of ionized regions Q_I. For the most common UV sources, this is obtained by averaging equation (5) over a large volume:

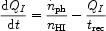(8)

where 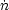_ph is average number of ionizing photons produced per unit volume per unit time. Note that the above equation implicitly assumes that the sources of radiation are distributed uniformly over the volume we are considering. The equation can be solved once we know the value and evolution of the photon production rate 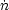_ph and also the clumping factor . One can get an estimate of 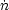_ph by assuming that it is proportional to the fraction of gas within collapsed haloes, while the value of is relatively difficult to calculate and is usually assumed to be somewhere between a few and 100. In this simple picture, reionization is said to be complete when Q_I reaches unity. Assuming a normal stellar population (i.e., a Salpeter-like IMF and standard stellar spectra obtained from population synthesis codes) and a value of 10-30, one obtains a reionization in the redshift range between 6 and 10 [142].

This approach can be improved if the density inhomogeneities of the IGM are taken into account. In the above picture, the inhomogeneities in the IGM are considered simply in terms of the clumping factor in the effective recombination timescale without taking into account the density distribution of the IGM. The importance of using a density distribution of the IGM lies in the fact that regions of lower densities will be ionized first, and high-density regions will remain neutral for a longer time. The main reason for this is that the recombination rate is higher in high-density regions where the gas becomes neutral very quickly ⁵. Thus, in the situation where all the individual ionized regions have overlapped (the so-called post-overlap stage), all the low-density regions (with overdensities, say, < _i) will be highly ionized, while there will be some high density peaks (like the collapsed systems) which will still remain neutral. The situation is slightly more complicated when the ionized regions are in the pre-overlap stage. At this stage, it is assumed that a volume fraction 1 - Q_I of the universe is completely neutral (irrespective of the density), while the remaining Q_I fraction of the volume is occupied by ionized regions. However, within this ionized volume, the high density regions (with > _I) will still be neutral. Once Q_I becomes unity, all regions with < _I are ionized and the rest are neutral. The high-density neutral regions manifest themselves as the Lyman-limit systems (i.e., systems with neutral hydrogen column densities N_HI > 10¹⁷ cm^-2) in the QSO absorption spectra. The reionization process after this stage is characterized by increase in _I - implying that higher density regions are getting ionized gradually [45].

To develop the equations embedding the above physical picture, we need to know the probability distribution function P() d for the overdensities. Given a P() d, it is clear that only a mass fraction

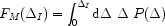(9)

needs be ionized, while the remaining high density regions will be completely neutral because of high recombination rates. The generalization of equation (5), appropriate for this description is given by [45, 143]

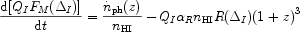(10)

The factor R(_I) is the analogous of the clumping factor, and is given by

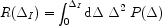(11)

The reionization is complete when Q_I = 1; at this point a mass fraction F_M(_I) is ionized, while the rest is (almost) completely neutral.

Note that this approach not only takes into account all the three stages of reionization, but also computes the clumping factor in a self-consistent manner. This approach has been combined with the evolution of thermal and ionization properties of the IGM [144] to predict various properties related to reionization and then compare with observations. By constraining the model free parameters with available data on redshift evolution of Lyman-limit absorption systems, GP and electron scattering optical depths, and cosmic star formation history, a unique reionization model can be identified, whose main predictions are: Hydrogen was completely reionized at z 15, while helium must have been doubly ionized by z 12 by the metal-free PopIII stars. Interestingly only 0.3 per cent of the stars produced by z = 2 need to be PopIII stars in order to achieve the first hydrogen reionization. At z 7 - 10, the doubly ionized helium suffered an almost complete recombination as a result of the extinction of PopIII stars. A QSO-induced complete helium reionization occurs at z 3.5; a similar double hydrogen reionization does not take place due to the large number of photons with energies > 13.6 eV from normal PopII stars and QSOs, even after all PopIII stars have disappeared. Following reionization, the temperature of the IGM corresponding to the mean gas density, T₀, is boosted to 1.5 × 10⁴ K; following that it decreases with a relatively flat trend. Observations of T₀ are consistent with the fact that helium is singly ionized at z 3.5, while they are consistent with helium being doubly ionized at z 3.5. This might be interpreted as a signature of (second) helium reionization. However, it is useful to remember that there could be other contributions to the ionizing background, like for example, because of thermal emission from gas shock heated during cosmic structure formation [145]. Such emission is characterized by a hard spectrum extending well beyond 54.4 eV and is comparable to the QSO intensity at z 3. These thermal photons alone could be enough to produce and sustain double reionization of helium already at z = 6. The observations of the state of helium at these intermediate redshifts (3 < z < 6) could be crucial to assess the nature of ionizing background arising from different sources.

None of the above models take into account the clustering of the sources (galaxies) in computing the growth of the volume filling factor of ionized regions. It is well known that the galaxies would form in high-density regions which are highly correlated. The overlap of the ionized bubbles and hence the morphology of the ionized regions would then be determined by the galaxy clustering pattern; for example, the sizes of the ionized bubbles could be substantially underestimated if the correlation between the sources are not taken into account. The first approach to treat this has been to use an approach based on the excursion set formalism (similar to the Press-Schechter approach in spirit) to calculate the growth and size distribution of ionized regions [146]. It can be shown that the sizes of the ionized regions can be larger than ~ 10 comoving Mpcs when the ionization fraction of the IGM is 0.5-1.0 [93]. This highlights the fact that it is quite difficult to study overlap of ionized regions with limited box size in numerical simulations (which are often less that 10 comoving Mpc). The other important result which can be drawn from such analyses is that the reionization can be a very inhomogeneous process; the overlap of bubbles would be completed in different portions of the IGM at different epochs depending on the density inhomogeneities in that region.

3.2. Simulations

Though the analytical studies mentioned above allow us to develop a good understanding of the different processes involved in reionization, they can take into account the physical processes only in some approximate sense. In fact, a detailed and complete description of reionization would require locating the ionizing sources, resolving the inhomogeneities in the IGM, following the scattering processes through detailed radiative transfer, and so on. Numerical simulations, in spite of their limitations, have been of immense importance in these areas.

The greatest difficulty any simulation faces while computing the growth of ionized regions is to solve the radiative transfer equation [147]

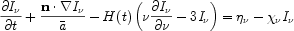(12)

where I I(t, x, n, ) is the monochromatic specific intensity of the radiation field, n is a unit vector along the direction of propagation of the ray, H(t) is the Hubble parameter, and is the ratio of cosmic scale factors between photon emission at frequency and the time t. Here and denote the emission coefficient and the absorption coefficient, respectively. The denominator in the second term accounts for the changes in path length along the ray due to cosmic expansion, and the third term accounts for cosmological redshift and dilution.

In principle, one could solve equation (12) directly for the intensity at every point in the seven-dimensional (t, x, n, ) space, given the coefficients and . However, the high dimensionality of the problem makes the solution of the complete radiative transfer equation well beyond our capabilities, particularly since we do not have any obvious symmetries in the problem and often need high spatial and angular resolution in cosmological simulations. Hence, the approach to the problem has been to use different numerical schemes and approximations, like ray-tracing [147, 148, 149, 150, 151, 152, 153, 154, 155], Monte Carlo methods [156, 157], local depth approximation [68] and others.

Since the radiative transfer is computationally extremely demanding, most efforts have been concentrating on small regions of space (~ 10-50 comoving Mpc). The main reason for this limitation is that the ionizing photons during early stages of reionization mostly originate from smaller haloes which are far more numerous than the larger galaxies at high redshifts. The need to resolve such small structures imposes a severe limit on the computational box size. On the other hand, these ionizing sources were strongly clustered at high redshifts and, as a consequence, the ionized regions they created are expected to overlap and grow to very large sizes, reaching upto tens of Mpc [158, 93, 159]. As already discussed, the many orders of magnitude difference between these length scales demand extremely high computing power from any simulations designed to study early structure formation from the point of view of reionization. Further limitations are imposed by the method used in the radiative transfer schemes; for most of them the computational expense grows roughly proportionally to the number of ionizing sources present. This generally makes the radiative transfer solution quite inefficient when more than a few thousand ionizing sources are involved, severely limiting the computational volume that can be simulated effectively. However these methods can be useful and quite accurate in certain special circumstances like, say, to study the growth of ionized regions around an isolated source.

A closely related problem which can be dealt with in numerical simulations is that of the clumpiness of the IGM. We have already discussed on how the density inhomogeneities can play an important role in characterising reionization. Various hydrodynamical simulations have been carried out using sophisticated tools to generate the density distribution of gas over large ranges of spatial and density scales. This, when combined with radiative transfer schemes, can give us an idea about the propagation of ionization fronts into an inhomogeneous medium, which is otherwise a very difficult problem. Using radiative transfer simulations over large length scales (~ 150 comoving Mpc) based on explicit photon conservation in space and time [155], quite a few conclusions about the nature of reionization (by UV sources) can be drawn. For example, it is likely that reionization proceeded in an inside-out fashion, with the high-density regions being ionized earlier, on average, than the voids. This has to do with the fact that most ionizing sources reside inside a high density halo. Interestingly, ionization histories of smaller-size (5 to 10 comoving Mpc) subregions exhibit a large scatter about the mean and do not describe the global reionization history well, thus showing the importance of large box sizes. The minimum reliable volume size for such predictions is found to be ~ 30 Mpc. There seems to be two populations of ionized regions according to their size: numerous, mid-sized (~ 10 Mpc) regions and a few, rare, very large regions tens of Mpc in size. The statistical distributions of the ionized fraction and ionized gas density at various scales show that both distributions are clearly non-Gaussian, indicating the non-linearities in the problem.

There is thus quite good progress in studying the growth of the ionized regions, particularly those due to UV sources, and also the qualitative features for the global reionization seem to be understood well. The number of unanswered questions still do remain large, particularly those related to the feedback effects. The expectation is that as more observations come up, the physics of the models would be nicely constrained and a consistent picture of reionization is obtained. We shall review the future prospects for this field in the next Section.

⁴ The propagation of singly-ionized helium front coincides with the hydrogen ionization front for almost all forms of the ionizing spectrum. Hence, as far as helium is concerned, most studies are concerned with the propagation of the doubly-ionized helium fronts. Back.

⁵ Of course, there will be a dependence on how far the high density region is from an ionizing source; however such complexities can only be dealt in a full numerical simulation. Back.