In the final Section, we review certain observations which will shape our understanding of reionization in near future, and also discuss the theoretical predictions concerning future data sets.
The spectroscopic studies of QSOs at z
6 hold
promising prospects for determining the neutrality of the IGM.
As we have discussed in Section 2, regions with high transmission in the
Ly
forest
become rare at high redshifts. Therefore the standard methods of
analyzing the
Ly forest (like the
probability distribution function and power spectrum) are
not very effective. An alternative method to analyze the
statistical properties of the transmitted flux is the distribution
of dark gaps
[160,
91],
defined as contiguous regions of the spectrum having an optical depth
above a threshold value (say 2.5
[91]
or 3.5
[90]).
The frequency and the width of the gaps are expected to increase
with redshift, which is verified in different analyses of observational
data [91,
90].
However, it is more interesting to check whether
the dark gap width distribution (DGWD) is at all sensitive to the
reionization history of the IGM, and whether one can constrain
reionization through DGWD. This is indeed possible as it is found
by semi-analytical models and simulations of
Ly forest
at z
6
[161].
In particular, about 30 per cent of the lines of sight (accounting for
statistical and systematic uncertainties)
in the range z = 5.7 - 6.3 are expected to have
dark gaps of widths larger than 60 Å (in the QSO rest frame) if the
IGM is in the pre-overlap stage at z
6, while no lines
of sight should have such large gaps if the IGM is already ionized.
The constraints become more stringent at higher redshifts.
Furthermore, 10 lines of sight should be sufficient for the DGWD to give
statistically robust results and discriminate between early and late
reionization scenarios. It is expected that the SDSS and Palomar-Quest
survey
[162]
would detect ~ 30 QSOs at
these redshifts within the next few years and hence we expect
robust conclusions from DGWD in very near future.
As we have discussed already, the first evidence for an early
reionization epoch came from the CMB polarization data. This
data is going to be much more precise in future with
experiments like PLANCK,
6
and is expected to improve the
constraints on 
el.
With improved statistical errors,
it might be possible to distinguish between different evolutions
of the ionized fraction, particularly with E-mode polarization
auto-correlation, as is found from theoretical calculations
[163].
An alternative option to probe reionization through CMB
is through the small scale observations of temperature anisotropies.
It has been well known that the scattering of the CMB photons
by the bulk motion of the electrons in clusters gives rise to a signal
at large 
, known as the
kinetic Sunyaev-Zeldovich (SZ) effect:
 |
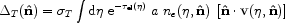(13) |
where 
=
dt /
a is the conformal time, v is the peculiar velocity field and
ne is the number density of electrons.
In principle, a signal should arise from the
fluctuations in the distribution of free electrons
arising from cosmic reionization.
Now, if the reionization is uniform, the only fluctuations
in ne can arise from the baryonic density fluctuations
, and
hence the power spectrum of temperature anisotropies
C would be mostly determined by
correlation terms like
<
v
v
>.
Though this can give
considerable signal (an effect known as the Ostriker-Vishniac
effect), particularly for the non-linear densities, it turns out that
for reionization the signal is dominated by the patchiness in the
ne distribution. In other words, if
xe
denotes the fluctuations in the
ionization fraction of the IGM, the correlation term
<
xe
v
xe
v >
(i.e., correlations of
the ionization fraction fluctuations and the large-scale bulk flow)
gives the dominant contribution to the temperature anisotropies
C.
Now, in most scenarios of reionization, it is expected that
the distribution of neutral hydrogen would be quite
patchy in the pre-overlap era, with the ionized hydrogen
mostly contained within isolated bubbles.
The amplitude of this signal is significant around
~ 1000 and is usually
comparable to or greater than the signal arising from standard kinetic
SZ effect (which, as mentioned earlier, is related to the scattering of
the CMB photons by the bulk motion of the electrons in clusters).
Theoretical estimates of the signal have been performed
for various reionization scenarios, and it has been predicted that
the experiment can be used for constraining reionization history
[164,
165].
Also, it is possible to have an idea about the nature of reionization
sources, as the signal from UV sources, X-ray sources and
decaying particles are quite different. With multi-frequency
experiments like Atacama Cosmology Telescope (ACT)
7
and South Pole Telescope (SPT)
8 coming up in near
future, this promises to put strong constraints on the reionization
scenarios.
Another interesting prospect for constraining reionization is
through high redshift energetic sources like gamma ray bursts (GRBs)
and supernovae. There are different ways of using these sources
for studying reionization.
The first is to study the spectra of individual sources and
estimate the neutral fraction of hydrogen through its
damping wing effects. This is similar to what is done in the
case of Ly emitters as
discussed in Section 2.
The damping wing of the surrounding neutral medium,
if strong enough, would suppress the spectrum
at wavelengths redward of the Lyman break. In fact, analyses
have been already performed on the GRB with highest detected
redshift (zem = 6.3), and the wing shape is well-fit
by a neutral fraction xHI = 0.00 ± 0.17
[166].
In order to obtain more stringent limits on reionization,
it is important to increase the sample size of z
6 GRBs.
Given a reionization model, one can actually calculate the
number of GRB afterglows in the pre-reionization era
which would be highly absorbed by the neutral hydrogen.
These GRBs would then be categorised as
"dark" GRBs (i.e., GRBs without afterglows), and the
redshift distribution of such objects can give us a good handle
on the evolution of the neutral hydrogen in the universe
[167,
168].
The second way in which GRBs could be used is to constrain the
star formation history, and hence get indirect constraints on
reionization. In most popular models of GRBs, it is assumed that they
are related to collapse of massive stars (just like supernovae),
and hence could be nice tracers of star formation.
In fact, one can write the number of GRBs (or supernovae) per
unit redshift range observed over a time
tobs as
[167,
169]
 |
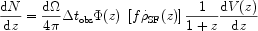(14) |
where the factor (1 + z) is due to the time dilation between
z and the present epoch, dV(z) is the comoving volume
element, d 
/
4 
is the mean
beaming factor and 
(z) is the
weight factor due to the limited sensitivity of the detector, because of
which, only brightest bursts will be observed at higher redshifts.
The quantity f is an efficiency factor which links the formation
of stars 
SF (z)
to that of GRBs (or supernovae); it corresponds to the number of GRBs
(supernovae)
per unit mass of forming stars, hence it depends on the fraction of
mass contained in (high mass) stars which are potential progenitors
of the GRBs (supernovae). Clearly, the value of f might depend
on some details of GRB formation and is expected to be quite
sensitive to the stellar IMF. Though such details still
need to be worked out, it seems promising that data on the
redshift distribution of GRBs and supernovae could give a handle
on the star formation rate, which in turn could give us insights
on quantities like efficiency of molecular cooling or the
relative contribution of minihaloes to radiation.
In general, the GRB rates at high redshifts should be able
to tell us how efficient stars were in ionizing the IGM.
Perhaps the most promising prospect of detecting the fluctuations in the neutral hydrogen density during the (pre-)reionization era is through the future 21 cm emission experiments [170] like LOFAR 9. The basic principle which is central to these experiments is the neutral hydrogen hyperfine transition line at a rest wavelength of 21 cm. This line, when redshifted, is observable in radio frequencies (~ 150 MHz for z ~ 10) as a brightness temperature:
 |
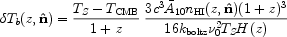(15) |
where TS is the spin temperature of the gas,
TCMB = 2.76 (1 + z) K
is the CMB temperature, A10 is the Einstein coefficient
and 
0 = 1420 MHz is
the rest frequency of the hyperfine line.
The expression can be simplified to
 |
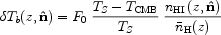(16) |
with
 |
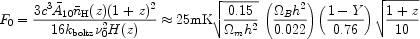(17) |
The observability of this brightness temperature against the
CMB background will depend on the relative values
of TS and TCMB. Depending on which
processes
dominate at different epochs, TS will couple
either to radiation (TCMB) or to matter (determined
by the kinetic temperature Tk). There are four broad
eras characterising the spin temperature
[171,
172]:
(i) At z
30, the density of matter is high enough to make collisional
coupling dominant, hence TS is coupled to
Tk. However, at z
100, the gas
temperature is coupled strongly to TCMB, thus making
TS 
Tk
TCMB. At these epochs, the
21 cm radiation is not observable. (ii) At
30 
z
100,
the kinetic temperature falls off adiabatically and hence is lower than
TCMB, while TS is still
collisionally coupled
to Tk. This would imply that the 21 cm radiation will
be observed in absorption against CMB. (iii) Subsequently
the radiative coupling would take over and make
TS = TCMB,
thus making the brightness temperature vanish. This continues
till the sources turn up and a
Ly background is
established. (iv) Once there is background of
Ly photons, that
will couple TS again to Tk through
the Wouthuysen-Field mechanism. From
this point on, the 21 cm radiation will be observed either
in emission or in absorption depending on whether
Tk is higher or lower than TCMB,
which turns out be highly model-dependent.
Almost in all models of reionization, the most interesting phase
for observing the 21 cm radiation is
6 z
20. This
is the phase where the IGM is suitably heated to temperatures
much higher than CMB (mostly due to X-ray heating
[141])
thus making it observable in emission. Furthermore, this is the era when
the bubble-overlapping phase is most active, and there is substantial
neutral hydrogen to generate a strong enough signal. At low
redshifts, after the IGM is reionized, nHI falls by orders
of magnitude and the 21 cm signal vanishes.
Most theoretical studies are concerned with studying the angular
power spectrum of the brightness temperature fluctuations, which
is essentially determined by the correlation terms
< 
Tb
Tb >. It is clear from equation
(16) that the temperature power spectrum is
directly related to the power spectrum of neutral hydrogen, i.e.,
< nHI nHI >. This then turns
out to be a direct probe of the neutral hydrogen distribution, and
potentially can track the evolution of the patchiness in the distribution
over redshift. In fact, one expects a peak in the signal on angular scales
corresponding to the characteristic size of the ionized bubbles.
While there are some significant systematics which have
to be controlled (say, for example, the foregrounds), the
experiments do promise a revolution in our understanding of reionization.
There are interesting ways in which one can combine signals from
different experiments too. For example, an obvious step would be
to calculate the correlation between CMB signal from
kinetic SZ effect and the 21 cm brightness temperatures
< T
Tb >.
This will essentially be determined by the correlations
< ne nHI v >
[173].
It is expected, that the ionized number density ne will
be highly anti-correlated with the neutral
number density nHI. In fact, the simulations do
show a clear signal for this anti-correlation. Depending on the
angular scales of anti-correlation, one can actually re-construct the
sizes of the bubbles as a function of redshift and thus
compute the reionization history
[174].
We hope to have convinced the reader that we are about to enter the most exciting phase in the study of reionization as new observations with LOFAR, ALMA and NGWST will soon settle the long-standing question on when and how the Universe was reionized. From the theoretical point of view, it is thereby important to develop detailed analytical and numerical models to extract the maximum information about the physical processes relevant for reionization out of the expected large and complex data sets.
6 http://www.rssd.esa.int/Planck/ Back
7 http://www.hep.upenn.edu/act/ Back
8 http://spt.uchicago.edu/ Back