9. BLACK HOLES AND SOLITONS

9.1. Primordial black holes

At first glance, black holes would appear to be among the unlikeliest of background radiation sources. In fact, experimental data on the intensity of the EBL constrain black holes more strongly than any of the dark-matter candidates we have discussed so far. Before explaining how this comes about, we distinguish between "ordinary" black holes (which form via the gravitational collapse of massive stars at the end of their lives) and primordial black holes (PBHs) which may have arisen from the collapse of overdense regions in the early Universe. The existence of the former is very nearly an established fact, while the latter remain hypothetical. However, it is PBHs which are of interest to us as potential dark-matter candidates.

The reason for this is as follows. Ordinary black holes come from baryonic progenitors (i.e. stars) and are hence classified with the baryonic dark matter of the Universe. (They are of course not "baryonic" in other respects, since among other things their baryon number is not defined.) Ordinary black holes are therefore subject to the nucleosynthesis bound (94), which limits them to less than 5% of the critical density. PBHs are not subject to this bound because they form during the radiation-dominated era, before nucleosynthesis begins. Nothing prevents them from making up most of the density in the Universe. Moreover they constitute cold dark matter because their velocities are low. (That is, they collectively obey a dust-like equation of state, even though they might individually be better described as "radiation-like" than baryonic.) PBHs were first proposed as dark-matter candidates by Zeldovich and Novikov in 1966 [394] and Hawking in 1971 [395].

Black holes contribute to the EBL via a process discovered by Hawking in 1974 and often called Hawking evaporation [396]. Photons cannot escape from inside the black hole, but they are produced at or near the horizon by quantum fluctuations in the surrounding curved spacetime. These give rise to a net flux of particles which propagates outward from a black hole (of mass M) at a rate proportional to M^-2 (with the black-hole mass itself dropping at the same rate). For ordinary, stellar-mass black holes, this process occurs so slowly that contributions to the EBL are insignificant, and the designation "black" remains perfectly appropriate over the lifetime of the Universe. PBHs, however, can in principle have masses far smaller than those of a star, leading to correspondingly higher luminosities. Those with M 10¹⁵ g (the mass of a small asteroid) would in fact evaporate quickly enough to shed all their mass over less than ~ 10 Gyr. They would already have expired in a blaze of high-energy photons and other elementary particles as M 0.

We will use the PBHs themselves as sources of radiation in what follows, taking them to be distributed homogeneously throughout space. The degree to which they actually cluster in the potential wells of galaxies and galaxy clusters is not of concern here, since we are concerned with their combined PBH contributions to the diffuse background. Another subtlety must, however, be taken into account. Unlike the dark-matter halos of previous sections, PBHs cover such a wide range of masses (and luminosities) that we can no longer treat all sources as identical. Instead we must define quantities like number density and energy spectrum as functions of PBH mass as well as time, and integrate our final results over both parameters.

The first step is to identify the distribution of PBH masses at the time when they formed. There is little prospect of probing the time before nucleosynthesis experimentally, so any theory of PBH formation is necessarily speculative to some degree. However, the scenario requiring the least extrapolation from known physics would be one in which PBHs arose via the gravitational collapse of small initial density fluctuations on a standard Robertson-Walker background, with an equation of state with the usual form (27), and with initial density fluctuations distributed like

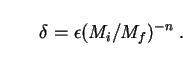(257)

Here M_i is the initial mass of the PBH, M_f is the mass lying inside the particle horizon (or causally connected Universe) at PBH formation time, and is an unknown proportionality constant.

PBH formation under these conditions was originally investigated by Carr [397], who showed that the process is favoured over an extended range of masses only if n = 2/3. Proceeding on this assumption, he found that the initial mass distribution of PBHs formed with masses between M_i and M_i + dM_i per unit comoving volume is

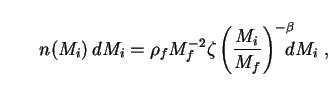(258)

where _f is the mean density at formation time. The parameters and are formally given by 2(2 - 1) / and exp[- ( - 1)² / 2²] respectively, where is the equation-of-state parameter as usual. However, in the interests of lifting every possible restriction on conditions prevailing in the early Universe, we follow Carr [398] in treating and as free parameters, not necessarily related to and . Insofar as the early Universe was governed by the equation of state (27), takes values between 2 (dust-like or "soft") and 3 (stiff or "hard"), with = 5/2 corresponding to the most natural situation (i.e. = 4/3 as for a non-interacting relativistic gas). We allow to take values as high as 4, corresponding to "superhard" early conditions. The parameter represents the fraction of the Universe which goes into PBHs of mass M_f at time t_f. It is a measure of the initial inhomogeneity of the Universe.

The fact that Eq. (258) has no exponential cutoff at high mass is important because it allows us (in principle at least) to obtain a substantial cosmological density of PBHs. Since 2 4, however, the power-law distribution is dominated by PBHs of low mass. This is the primary reason why PBHs turn out to be so tightly constrained by data on background radiation. It is the low-mass PBHs whose contributions to the EBL via Hawking evaporation are the strongest.

Much subsequent effort has gone into the identification of alternative formation mechanisms which could give rise to a more favourable distribution of PBH masses (i.e. one peaked at sufficiently high mass to provide the requisite CDM density without the unwanted background radiation from the low-mass tail). For example, PBHs might arise from a post-inflationary spectrum of density fluctuations which is not perfectly scale-invariant but has a characteristic length scale of some kind [399]. The parameter in (258) would then depend on the inflationary potential (or analogous quantities). This kind of dependence has been discussed in the context of two-stage inflation [400], extended inflation [401], chaotic inflation [402], "plateau" inflation [403], hybrid inflation [404] and inflation with isocurvature fluctuations [405].

A narrow spectrum of masses might also be expected if PBHs formed during a spontaneous phase transition rather than arising from primordial fluctuations. The quark-hadron transition [406], grand unified symmetry-breaking transition [407] and Weinberg-Salam phase transition [408] have all been considered in this regard. The initial mass distribution in each case would be peaked near the horizon mass M_f at transition time. The quark-hadron transition has attracted particular attention because PBH formation would be enhanced by a temporary softening of the equation of state; and because M_f for this case is coincidentally close to M, so that PBHs formed at this time might be responsible for MACHO observations of microlensing in the halo [409]. Cosmic string loops have also been explored as possible seeds for PBHs with a peaked mass spectrum [410, 411]. Considerable interest has recently been generated by the discovery that PBHs could provide a physical realization of the theoretical phenomenon known as critical collapse [412]. If this is so, then initial PBH masses would no longer necessarily be clustered near M_f.

While any of the above proposals can in principle concentrate the PBH population within a narrow mass range, all of them face the same problem of fine-tuning if they are to produce the desired present-day density of PBHs. In the case of inflationary mechanisms it is the form of the potential which must be adjusted. In others it is the bubble nucleation rate, the string mass per unit length, or the fraction of the Universe going into PBHs at formation time. Thus, while modifications of the initial mass distribution may weaken the "standard" constraints on PBH properties (which we derive below), they do not as yet have a compelling physical basis. Similar comments apply to attempts to link PBHs with specific observational phenomena. It has been suggested, for instance, that PBHs with the right mass could be responsible for certain classes of -ray bursts [413, 414, 415], or for long-term quasar variability via microlensing [416, 417]. Other possible connections have been drawn to diffuse -ray emission from the Galactic halo [418, 419] and the MACHO microlensing events [420, 421]. All of these suggestions, while intriguing, would beg the question: "Why this particular mass scale?"

9.2. Evolution and density

In order to obtain the comoving number density of PBHs from their initial mass distribution, we use the fact that PBHs evaporate at a rate which is inversely proportional to the square of their masses:

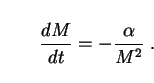(259)

This applies to uncharged, non-rotating black holes, which is a reasonable approximation in the case of PBHs since these objects discharge quickly relative to their lifetimes [422] and also give up angular momentum by preferentially emitting particles with spin [423]. The parameter depends in general on PBH mass M and its behaviour was worked out in detail by Page in 1976 [424]. The most important PBHs are those with 4.5 × 10¹⁴ g M 9.4 × 10¹⁶ g. Black holes in this range are light (and therefore "hot") enough to emit massless particles (including photons) as well as ultra-relativistic electrons and positrons. The corresponding value of is

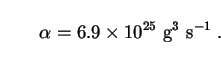(260)

For M > 9.4 × 10¹⁶ g, the value of drops to 3.8 × 10²⁵ g³ s^-1 because the larger black hole is "cooler" and no longer able emit electrons and positrons. EBL contributions from PBHs of this mass are however of lesser importance because of the shape of the mass distribution.

As the PBH mass drops below 4.5 × 10¹⁴ g, its energy kT climbs past the rest energies of progressively heavier particles, beginning with muons and pions. As each mass threshold is passed, the PBH is able to emit more particles and the value of increases further. At temperatures above the quark-hadron transition (kT 200 MeV), MacGibbon and Webber have shown that relativistic quark and gluon jets are likely to be emitted rather than massive elementary particles [425]. These jets subsequently fragment into stable particles, and the photons produced in this way are actually more important (at these energies) than the primary photon flux. The precise behaviour of in this regime depends to some extent on one's choice of particle physics. A plot of (M) for the standard model is found in the review by Halzen [426], who note that climbs to 7.8 × 10²⁶ g³ s^-1 at kT = 100 GeV, and that its value would be at least three times higher in supersymmetric extensions of the standard model where there are many more particle states to be emitted.

As we will shortly see, however, EBL contributions from PBHs at these temperatures are suppressed by the fact that the latter have already evaporated. If we assume for the moment that PBH evolution is adequately described by (259) with = constant as given by (260), then integration gives

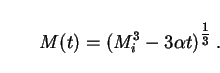(261)

The lifetime t_pbh of a PBH is found by setting M(t_pbh) = 0, giving t_pbh = M_i³ / 3. Therefore the initial mass of a PBH which is just disappearing today (t_pbh = t₀) is given by

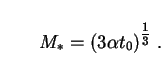(262)

Taking t₀ = 16 Gyr and using (260) for , we find that M_* = 4.7 × 10¹⁴ g. A numerical analysis allowing for changes in the value of over the full range of PBH masses with 0.06 _m,0 1 and 0.4 h₀ 1 leads to a somewhat larger result [426]:

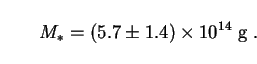(263)

PBHs with M M_* are exploding at redshift z 0 and consequently dominate the spectrum of EBL contributions. The parameter M_* is therefore of central importance in what follows.

We now obtain the comoving number density of PBHs with masses between M and M + dM at any time t. This is the same as the comoving number density of PBHs with initial masses between M_i and M_i + dM_i at formation time, so n(M, t) dM = n(M_i) dM_i. Inverting Eq. (261) to get M_i = (M³ + 3 t)^1/3 and differentiating, we find from (258) that

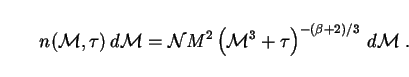(264)

Here we have used (262) to replace M_*³ with 3 t₀ and switched to dimensionless parameters M / M_* and t / t₀. The quantity is formally given in terms of the parameters at PBH formation time by = ( _f / M_f)(M_f / M_*)^-1 and has the dimensions of a number density. As we will see shortly, it corresponds roughly to the comoving number density of PBHs of mass M_*. Following Page and Hawking [427], we allow to move up or down as required by observational constraints. The theory to this point is thus specified by two free parameters: the PBH normalization and the equation-of-state parameter .

To convert to the present mass density of PBHs with mass ratios between and + d, we multiply Eq. (264) by M = M_* and put = 1:

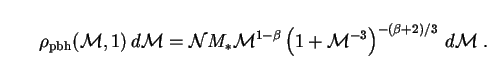(265)

The total mass in PBHs is then found by integrating over from zero to infinity. Changing variables to x ^-3, we obtain:

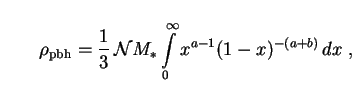(266)

where a 1/3( - 2) and b 4/3. The integral is solved to give

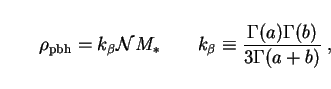(267)

where (x) is the gamma function. Allowing to take values from 2 through 5/2 (the most natural situation) and up to 4, we find that

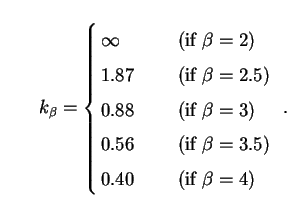(268)

The total mass density of PBHs in the Universe is thus _pbh M_*. Eq. (267) can be recast as a relation between the characteristic number density and the PBH density parameter _pbh = _pbh / _crit,0:

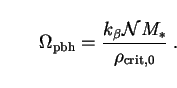(269)

The quantities and _pbh are thus interchangeable as free parameters. If we adopt the most natural value for (=2.5) together with an upper limit on due to Page and Hawking of 10⁴ pc^-3 [427], then Eqs. (24), (263), (268) and (269) together imply that _pbh is at most of order ~ 10^-8 h₀^-2. If this upper limit holds (as we confirm below, then there is little hope for PBHs to make up the dark matter.

Eq. (268) shows that one way to boost their importance would be to assume a soft equation of state at formation time (i.e. a value of close to 2 as for dust-like matter, rather than 2.5 as for radiation). Physically this is related to the fact that low-pressure matter offers little resistance to gravitational collapse. Such a softening has been shown to occur during the quark-hadron transition [409], leading to significant increases in _pbh for PBHs which form at that time (subject to the fine-tuning problem noted in Sec. 9.1). For PBHs which arise from primordial density fluctuations, however, such conditions are unlikely to hold throughout the formation epoch. In the limit 2, Eq. (258) breaks down in any case because it becomes possible for PBHs to form on scales smaller than the horizon [397].

9.3. Spectral energy distribution

Hawking [428] proved that an uncharged, non-rotating black hole emits bosons (such as photons) in any given quantum state with energies between E and E + dE at the rate

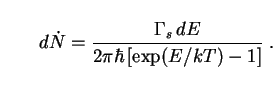(270)

Here T is the effective black-hole temperature, and _s is the absorption coefficient or probability that the same particle would be absorbed by the black hole if incident upon it in this state. The function d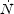 is related to the spectral energy distribution (SED) of the black hole by d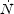 = F(, ) d / E, since we have defined F(, ) d as the energy emitted between wavelengths and + d. We anticipate that F will depend explicitly on the PBH mass as well as wavelength. The PBH SED thus satisfies

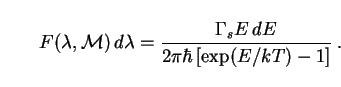(271)

The absorption coefficient _s is a function of and E as well as the quantum numbers s (spin), (total angular momentum) and m (axial angular momentum) of the emitted particles. Its form was first calculated by Page [424]. At high energies, and in the vicinity of the peak of the emitted spectrum, a good approximation is given by [429]

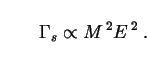(272)

This approximation breaks down at low energies, where it gives rise to errors of order 50% for (G M E / c³) ~ 0.05 [430] or (with E = 2 c / and M ~ M_*) for ~ 10^-3 Å. This is adequate for our purposes, as we will find that the strongest constraints on PBHs come from those with masses M ~ M_* at wavelengths ~ 10^-4 Å.

Putting (272) into (271) and making the change of variable to wavelength = hc / E, we obtain the SED

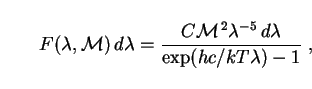(273)

where C is a proportionality constant. This has the same form as the blackbody spectrum, Eq. (78). We have made three simplifying assumptions in arriving at this result. First, we have neglected the black-hole charge and spin (as justified in Sec. 9.2). Second, we have used an approximation for the absorption coefficient _s. And third, we have treated all the emitted photons as if they are in the same quantum state, whereas in fact the emission rate (270) applies separately to the = s (= 1), = s + 1 and = s + 2 modes. There are thus actually three distinct quasi-blackbody photon spectra with different characteristic temperatures for any single PBH. However Page [424] has demonstrated that the = s mode is overwhelmingly dominant, with the = s + 1 and = s + 2 modes contributing less than 1% and 0.01% of the total photon flux respectively. Eq. (273) is thus a reasonable approximation for the SED of the PBH as a whole.

To fix the value of C we use the fact that the total flux of photons (in all modes) radiated by a black hole of mass M is given by [424]

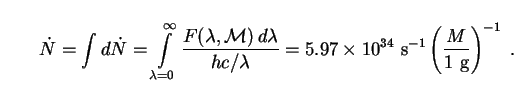(274)

Inserting (273) and recalling that M = M_* , we find that

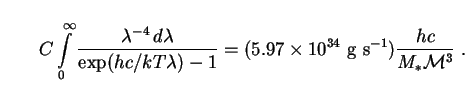(275)

The definite integral on the left-hand side of this equation can be solved by switching variables to = c / :

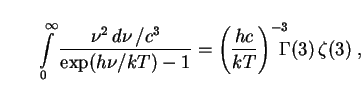(276)

where (n) and (n) are the gamma function and Riemann zeta function respectively. We then apply the fact that the temperature T of an uncharged, non-rotating black hole is given by

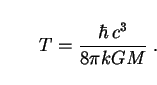(277)

Putting (276) and (277) into (275) and rearranging terms leads to

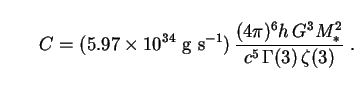(278)

Using (3) = 2! = 2 and (3) = 1.202 along with (263) for M_*, we find

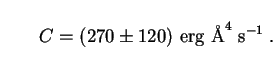(279)

We can also use the definitions (277) to define a useful new quantity:

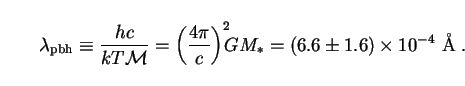(280)

The size of this characteristic wavelength tells us that we will be concerned primarily with the high-energy -ray portion of the spectrum. In terms of C and _pbh the SED (273) now reads

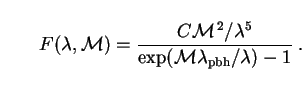(281)

While this contains no explicit time-dependence, the spectrum does of course depend on time through the PBH mass ratio . To find the PBH luminosity we employ Eq. (57), integrating the SED F(, ) over all to obtain:

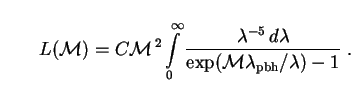(282)

This definite integral is also solved by means of a change of variable to frequency , with the result that

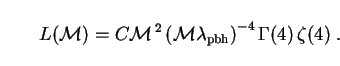(283)

Using Eqs. (263), (278) and (280) along with the values (4) = 3! = 6 and (4) = ⁴/96, we can put this into the form

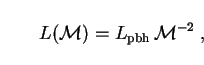(284)

where

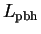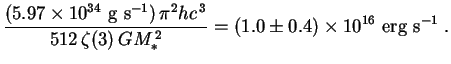Compared to the luminosity of an ordinary star, the typical PBH (of mass ratio 1) is not very luminous. A PBH of 900 kg or so might theoretically be expected to reach the Sun's luminosity; however, in practice it would already have exploded, having long since reached an effective temperature high enough to emit a wide range of massive particles as well as photons. The low luminosity of black holes in general can be emphasized by using the relation M / M_* to recast Eq. (284) in the form

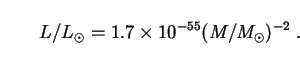(285)

This expression is not strictly valid for PBHs of masses near M, having been derived for those with M ~ M_* ~ 10¹⁵ g. (Luminosity is lower for larger black holes, and one of solar mass would be so much colder than the CMB that it would absorb radiation faster than it could emit it.) So, Hawking evaporation or not, most black holes are indeed very black.

9.4. Bolometric intensity

To obtain the total bolometric intensity of PBHs out to a look-back time t_f, we substitute the PBH number density (264) and luminosity (282) into the integral (12) as usual. Now however the number density n(t) is to be replaced by n(, ) d, L() takes the place of L(t), and we integrate over all PBH masses as well as look-back times :

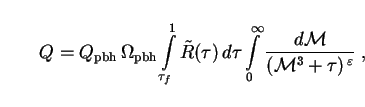(286)

where

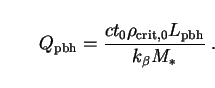(287)

Here ( + 2) / 3 and we have used (269) to replace with _pbh. In principle, the integral over should be cut off at a finite lower limit _c(), equal to the mass of the lightest PBH which has not yet evaporated at time . This arises because the initial PBH mass distribution (258) requires a nonzero minimum M_min in order to avoid divergences at low mass. In practice, however, the cutoff rapidly evolves toward zero from its its initial value of _c(0) = M_min / M_*. If M_min is of the order of the Planck mass as usually suggested [431], then _c() drops to zero well before the end of the radiation-dominated era. Since we are concerned with times later than this, we can safely set _c() = 0.

Eq. (286) can be used to put a rough upper limit on _pbh from the bolometric intensity of the background light [432]. Let us assume that the Universe is flat, as suggested by most observations (Sec. 4). Then its age t₀ can be obtained from Eq. (56) as

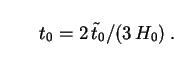(288)

Here 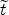_{0 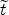m}(0) where 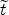_m(z) is the dimensionless function

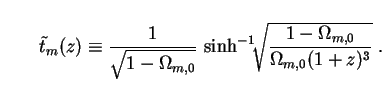(289)

Putting (288) into (287) and using Eqs. (18), (24), (263) and (284), we find:

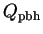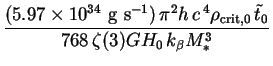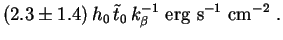			(290)

We are now ready to evaluate Eq. (286). To begin with we note that the integral over mass has an analytic solution:

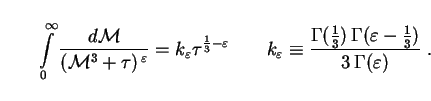(291)

For the EdS case (_m,0 = 1), 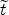₀ = 1 and Eq. (51) implies:

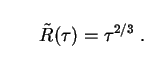(292)

Putting Eqs. (291) and (292) into (286), we find that

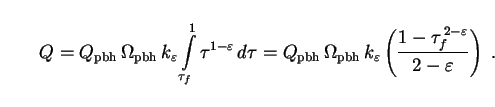(293)

The parameter _f is obtained for the EdS case by inverting (292) to give _f = (1 + z_f)^-3/2. The subscript "f" ("formation") is here a misnomer since we do not integrate back to PBH formation time, which occurred in the early stages of the radiation-dominated era. Rather we integrate out to the redshift at which processes like pair production become significant enough to render the Universe approximately opaque to the (primarily -ray) photons from PBH evaporation. Following Kribs [430] this is z_f 700.

Using this value of z_f and substituting Eqs. (290) and (291) into (293), we find that the bolometric intensity of background radiation due to evaporating PBHs in an EdS Universe is

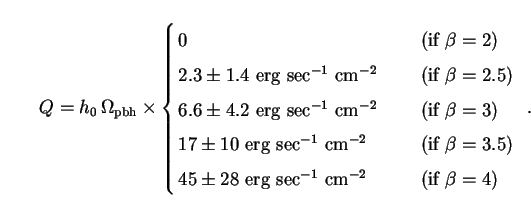(294)

This vanishes for = 2 because k in this limit, as discussed in Sec. 9.2. The case = 4 (i.e. = 2) is evaluated with the help of L'Hôpital's rule, which gives lim₂(1 - _f^2-) / (2 - ) = - ln_f.

The values of Q in Eq. (294) are far higher than the actual bolometric intensity of background radiation in an EdS universe, 2/5 Q_* = 1.0 × 10^-4 erg s^-1 cm^-2 (Fig. 2.6). Moreover this background is already well accounted for by known astrophysical sources. A firm upper bound on _pbh (for the most natural situation with = 2.5) is therefore

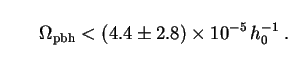(295)

For harder equations of state ( > 2.5) the PBH density would have to be even lower. PBHs in the simplest formation scenario are thus eliminated as important dark-matter candidates, even without reference to the cosmic -ray background.

For models containing dark energy as well as baryons and black holes, the integrated background intensity goes up because the Universe is older, and down because Q _pbh. The latter effect is stronger, so that the above constraint on _pbh will be weaker in a model such as CDM (with _m,0 = 0.3, _,0 = 0.7). To determine the importance of this effect, we can re-evaluate the integral (286) using the general formula (54) for 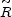() in place of (292). We will make the minimal assumption that PBHs constitute the only CDM, so that _m,0 = _pbh + _bar with _bar given by (94) as usual. Eq. (56) shows that the parameter _f is given for arbitrary values of _m,0 by _f = 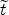_m(z_f) / 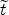₀ where the function 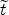_m(z) is defined as before by (289).

Evaluation of Eq. (286) leads to the plot of bolometric intensity Q versus _pbh in Fig. 40. As before, Q is proportional to h₀ because it goes as both _pbh = _{pbh crit,0} h₀² and t₀ h₀^-1. Since Q 0 for 2 we have chosen a minimum value of = 2.2 as representative of "soft" conditions. Fig. 40 confirms that, regardless of cosmological model, PBH contributions to the background light are too high unless _pbh << 1. The values in Eq. (294) are recovered at the right-hand edge of the figure where _pbh approaches one, as expected. For all other models, if we impose a conservative upper bound Q < Q_* (as indicated by the faint dotted line) then it follows that _pbh < (6.9 ± 4.2) × 10^-5h₀^-1 for = 2.5. This is about 60% higher than the limit (295) for the EdS case.

Figure 40. The bolometric intensity due to evaporating primordial black holes as a function of their collective density pbh and the equation-of-state parameter . We have assumed that m,0 = bar + pbh with bar = 0.016h0-2, h0 = 0.75 and ,0 = 1 - m,0. The horizontal dotted line indicates the approximate bolometric intensity (Q*) of the observed EBL.

9.5. Spectral intensity

Stronger limits on PBH density can be obtained from the -ray background, where these objects contribute most strongly to the EBL and where we have good data (as summarized in Sec. 8.6). Spectral intensity is found as usual by substituting the comoving PBH number density (264) and SED (281) into Eq. (61). As in the bolometric case, we now have to integrate over PBH mass as well as time = t / t₀, so that

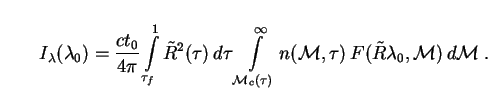(296)

Following the discussion in Sec. 9.4 we set _c() = 0. In light of our bolometric results it is unlikely that PBHs make up a significant part of the dark matter, so we no longer tie the value of _m,0 to _pbh. Models with _{m,0 bar} must therefore contain a second species of cold dark matter (other than PBHs) to provide the required matter density. Putting (264) and (281) into (296) and using (263), (269) and (278), we find that

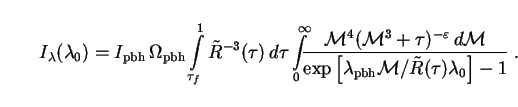(297)

Here the dimensional prefactor is a function of both and ₀ and reads

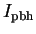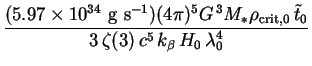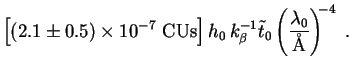			(298)

We have divided through by the photon energy hc / ₀ to put the results in units of CUs as usual. The range of uncertainty in I(₀) is smaller than that in Q, Eq. (290), because I(₀) depends only linearly on M_* whereas Q is proportional to M_*^-3. (This in turn results from the fact that I C M_* ² whereas Q L_pbh M_*^-2. One more factor of M_*^-1 comes from _pbh / M_* in both cases.) Like Q, I depends linearly on h₀ since integrated intensity in either case is proportional to both _{pbh crit,0} h₀² and t₀ h₀^-1.

Numerical integration of Eq. (297) leads to the plots shown in Fig. 41, where we have set _pbh = 10^-8. Following Page and Hawking [427] we have chosen values of _m,0 = 0.06 in panel (a) and _m,0 = 1 in panel (b). (Results are not strictly comparable in the former case, however, since we assume that _,0 = 1 - _m,0 rather than _,0 = 0.) Our results are in good agreement with the earlier ones except at the longest wavelengths (lowest energies), where PBH evaporation is no longer well described by a simple blackbody SED, and where the spectrum begins to be affected by pair production on nuclei. As expected the spectra peak near 10^-4 Å in the -ray region. Also plotted in Fig. 41 are the data from SAS-2 ([384]; heavy dashed line), COMPTEL ([382]; triangles) and EGRET ([385]; heavy solid line).

Figure 41. The spectral intensity of the diffuse -ray background from evaporating primordial black holes in flat models, as compared with experimental limits from SAS-2, COMPTEL and EGRET. Panel (a) assumes m,0 = 0.06, while Panel (b) is plotted for m,0 = 1 (the EdS case). All curves assume pbh = 10-8 and h0 = 0.75.

By adjusting the value of _pbh up or down from its value of 10^-8 in Fig. 41, we can match the theoretical PBH spectra to those measured (e.g., by EGRET), thereby obtaining the maximum value of _pbh consistent with observation. For = 2.5 this results in

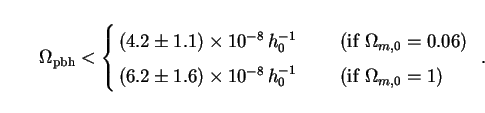(299)

These limits are three orders of magnitude stronger than the one from bolometric intensity, again confirming that PBHs in the simplest formation scenario cannot be significant contributors to the dark matter. Using (269) this result can be translated into an upper limit on :

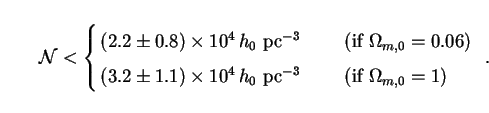(300)

These numbers are in good agreement with the original Page-Hawking bound of < 1 × 10⁴ pc^-3 [427], which was obtained for h₀ = 0.6.

Subsequent workers have refined the -ray background constraints on _pbh and in a number of ways. MacGibbon and Webber [425] pointed out that PBHs whose effective temperatures have climbed above the rest energy of hadrons probably give off more photons by indirect processes than by direct emission. This occurs because it is not bound states (i.e. hadrons) that are most likely to be emitted, but their elementary constituents (quarks and gluons in the form of relativistic jets). Accelerator experiments and numerical simulations indicate that these jets subsequently fragment into secondary particles whose decays (especially those of the pions) produce a far greater flux of photons than that emitted directly from the PBH. The net effect is to increase the PBH luminosity, particularly in low-energy -rays, strengthening the constraint on _pbh by about an order of magnitude [429]. The most recent upper limit obtained in this way using EGRET data (assuming _m,0 = 1) is _pbh < (5.1 ± 1.3) × 10^-9 h₀^-2 [433].

Complementary upper limits on PBH contributions to the dark matter have come from direct searches for those evaporating within a few kpc of the Earth. Such limits are subject to more uncertainty than ones based on the EBL because they depend on assumptions about the degree to which PBHs are clustered. If there is no clustering then (295) can be converted into a stringent upper bound on the local PBH evaporation rate, 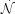< 10^-7 pc^-3 yr^-1. 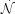This however relaxes to 10 pc^-3 yr^-1 if PBHs are strongly clustered [426], in which case limits from direct searches could potentially become competitive with those based on the EBL. Data taken at energies near 50 TeV with the CYGNUS air-shower array has led to a bound of 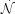< 8.5 × 10⁵ pc^-3 yr^-1 [434], and a comparable limit of 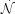< (3.0 ± 1.0) × 10⁶ pc^-3 yr^-1 has been obtained at 400 GeV using an imaging atmospheric Cerenkov technique developed by the Whipple collaboration [435]. Very strong constraints have also been claimed based on balloon observations of cosmic-ray antiprotons [436].

Other ideas have been advanced which could weaken the bounds on PBHs as dark-matter candidates. It might be, for instance, that these objects leave behind stable relics rather than evaporating completely [437], a possibility that has recently been revived on the grounds that total evaporation would be inconsistent with a generalized gravitational version of the uncertainty principle [438]. This however raises a new problem (similar to the "gravitino problem" discussed in Sec. 8.5) because such relics would have been overproduced by quantum and thermal fluctuations in the early Universe. Inflation can be invoked to reduce their density, but must be finely tuned if the same relics are to make up an interesting fraction of the dark matter today [439].

A different suggestion due to Heckler [440, 441] has been that particles emitted from the black hole might interact strongly enough above a critical temperature to form a photosphere. This would make the PBH appear cooler as seen from a distance than its actual surface temperature, just as the solar photosphere makes the Sun appear cooler than its core. (In the case of the black hole, however, one has not only an electromagnetic photosphere but a QCD "gluosphere.") The reality of this effect is still under debate [433], but preliminary calculations indicate that it could reduce the intensity of PBH contributions to the -ray background by 60% at 100 MeV, and by as much as two orders of magnitude at 1 GeV [442].

Finally, as discussed already in Sec. 9.1, the limits obtained above can be weakened or evaded if PBH formation occurs in such a way as to produce fewer low-mass objects. The challenge faced in such proposals is to explain how a distribution of this kind comes about in a natural way. A common procedure is to turn the question around and use observational data on the present intensity of the -ray background as a probe of the original PBH formation mechanism. Such an approach has been applied, for example, to put constraints on the spectral index of density fluctuations in the context of PBHs which form via critical collapse [430] or inflation with a "blue" or tilted spectrum [443]. Thus, even should they turn out not to exist, primordial black holes provide a valuable window on conditions in the early Universe, where information is otherwise scarce.

9.6. Solitons

In view of the fact that conventional black holes are disfavoured as dark-matter candidates, it is worthwhile to consider alternatives. One of the simplest of these is the extension of the black-hole concept from the four-dimensional (4D) spacetime of general relativity to higher dimensions. Higher-dimensional relativity, also known as Kaluza-Klein gravity, has a long history and underlies modern attempts to unify gravity with the standard model of particle physics [444]. The extra dimensions have traditionally been assumed to be compact, in order to explain their non-appearance in low-energy physics. The past few years, however, have witnessed a surge of interest in non-compactified theories of higher-dimensional gravity [445, 446, 447]. In such theories the dimensionality of spacetime can manifest itself at experimentally accessible energies. We focus on the prototypical five-dimensional (5D) case, although the extension to higher dimensions is straightforward in principle.

Black holes are described in 4D general relativity by the Schwarzschild metric, which reads (in isotropic coordinates)

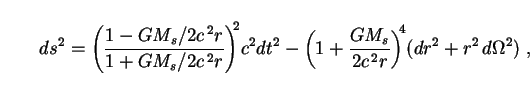(301)

where d² d² + sin² d ². This is a description of the static, spherically-symmetric spacetime around a pointlike object (such as a collapsed star or primordial density fluctuation) with Schwarzschild mass M_s. As we have seen, it is unlikely that such objects can make up the dark matter.

If the Universe has more than four dimensions, then the same object must be modelled with a higher-dimensional analog of the Schwarzschild metric. Various possibilities have been explored over the years, with most attention focusing on a 5D solution first discussed in detail by Gross and Perry [448], Sorkin [449] and Davidson and Owen [450] in the early 1980s. This is now generally known as the soliton metric and reads:

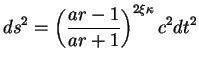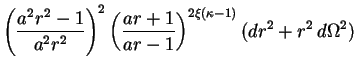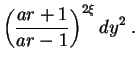			302

Here y is the new coordinate and there are three metric parameters (a, , ) rather than just one (M_s) as in Eq. (301). Only two of these are independent, however, because a consistency condition (which follows from the field equations) requires that ²(² - + 1) = 1. In the limit where 0, and 1, Eq. (302) reduces to (301) on 4D hypersurfaces y = const. In this limit we can also identify the parameter a as a = 2c² / GM_s where M_s is the Schwarzschild mass.

We wish to understand the physical properties of this solution in four dimensions. To accomplish this we do two things. First, we assume that Einstein's field equations in their usual form hold in the full five-dimensional spacetime. Second, we assume that the Universe in five dimensions is empty, with no 5D matter fields or cosmological constant. The field equations then simplify to

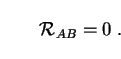(303)

Here _AB is the 5D Ricci tensor, defined in exactly the same way as the 4D one except that spacetime indices A, B run over 0-4 instead of 0-3. Putting a 5D metric such as (302) into the vacuum 5D field equations (303), we recover the 4D field equations (106) with a nonzero energy-momentum tensor _µ. Matter and energy, in other words, are induced in 4D by pure geometry in 5D. It is by studying the properties of this induced-matter energy-momentum tensor (_µ) that we learn what the soliton looks like in four dimensions.

The details of the mechanism just outlined [451] and its application to solitons in particular [452, 453] have been well studied and we do not review this material here. It is important to note, however, that the Kaluza-Klein soliton differs from an ordinary black hole in several key respects. It contains a singularity at its center, but this center is located at r = 1/a rather than r = 0. (The point r = 0 is, in fact, not even part of the manifold, which ends at r = 1 / a.) Its event horizon also shrinks to a point at r = 1 / a. For these reasons the soliton is better classified as a naked singularity than a black hole.

Solitons in the induced-matter picture are further distinguished from conventional black holes by the fact that they have an extended matter distribution rather than having all their mass compressed into the singularity. It is this feature which proves to be of most use to us in putting constraints on solitons as dark-matter candidates [454]. The time-time component of the induced-matter energy-momentum tensor gives us the density of the solitonic fluid as a function of radial distance:

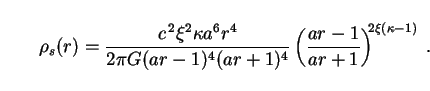(304)

From the other elements of _µ one finds that pressure can be written p_s = 1/3 _s c ², so that the soliton has a radiation-like equation of state. In this respect the soliton more closely resembles a primordial black hole (which forms during the radiation-dominated era) than one which arises as the endpoint of stellar collapse. The elements of _µ can also be used to calculate the gravitational mass of the fluid inside r:

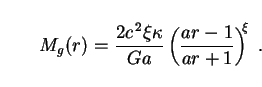(305)

At large distances r >> 1 / a from the center the soliton's density (304) and gravitational mass (305) go over to

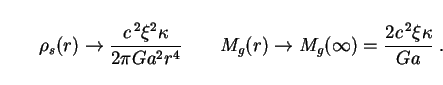(306)

The second of these expressions shows that the asymptotic value of M_g is in general not the same as M_s [M_g() = M_s for r >> 1 / a], but reduces to it in the limit 1. Viewed in four dimensions, the soliton resembles a hole in the geometry surrounded by a spherically-symmetric ball of ultra-relativistic matter whose density falls off at large distances as 1 / r⁴. If the Universe does have more than four dimensions, then objects like this should be common, being generic to 5D Kaluza-Klein gravity in exactly the same way that black holes are to 4D general relativity.

We therefore assess their impact on the background radiation, assuming that the fluid making up the soliton is in fact composed of photons (although one might also consider ultra-relativistic particles such as neutrinos in principle). We do not have spectral information on these so we proceed bolometrically. Putting the second of Eqs. (306) into the first gives

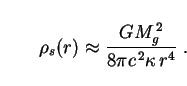(307)

Numbers can be attached to the quantities , r and M_g as follows. The first () is technically a free parameter. However, a natural choice from the physical point of view is ~ 1. For this case the consistency relation implies ~ 1 also, guaranteeing that the asymptotic gravitational mass of the soliton is close to its Schwarzschild one. To obtain a value for r, let us assume that solitons are distributed homogeneously through space with average separation d and mean density _s = _{s crit,0} = M_s / d³. Since _s drops as r^-4 whereas the number of solitons at a distance r climbs only as r³, the local density of solitons is largely determined by the nearest one. We can therefore replace r by d = (M_s / _{s crit,0})^1/3. The last unknown in (307) is the soliton mass M_g (= M_s if = 1). The fact that _s r^-4 is reminiscent of the density profile of the Galactic dark-matter halo, Eq. (174). Theoretical work on the classical tests of 5D general relativity [455] and limits on violations of the equivalence principle [456] also suggests that solitons are likely to be associated with dark matter on galactic or larger scales. Let us therefore express M_s in units of the mass of the Galaxy, which from (175) is M_gal 2 × 10¹² M. Eq. (307) then gives the local energy density of solitonic fluid as

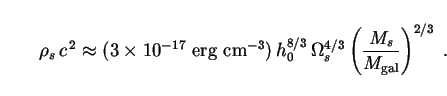(308)

To get a characteristic value, we take M_s = M_gal and adopt our usual values h₀ = 0.75 and _s = _cdm = 0.3. Let us moreover compare our result to the average energy density of the CMB, which dominates the spectrum of background radiation (Fig. 1). The latter is found from Eq. (141) as _cmb c ² = _crit,0 c ² = 4 × 10^-13 erg cm^-3. We therefore obtain

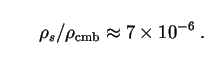(309)

This is of the same order of magnitude as the limit set on anomalous contributions to the CMB by COBE and other experiments. Thus the dark matter could consist of solitons, if they are not more massive than galaxies. Similar arguments can be made on the basis of tidal effects and gravitational lensing [454]. To go further and put more detailed constraints on these candidates from background radiation or other considerations will require a deeper investigation of their microphysical properties.

Let us summarize our results for this section. We have noted that standard (stellar) black holes cannot provide the dark matter insofar as their contributions to the density of the Universe are effectively baryonic. Primordial black holes evade this constraint, but we have reconfirmed the classic results of Page, Hawking and others: the collective density of such objects must be negligible, for otherwise their presence would have been obvious in the -ray background. In fact, we have shown that their bolometric intensity alone is sufficient to rule them out as important dark-matter candidates. These constraints may be relaxed if primordial black holes can form in such a way that they are distributed with larger masses, but it is not clear that such a distribution can be shown to arise in a natural way. As an alternative, we have considered black hole-like objects in higher-dimensional gravity. Bolometric arguments do not rule these out, but there are a number of theoretical issues to be worked out before a more definitive assessment of their potential can be made.