8. WEAKLY INTERACTING MASSIVE PARTICLES

8.1. The lightest supersymmetric particle

Weakly interacting massive particles (WIMPs) are as-yet undiscovered particles whose rest masses far exceed those of baryons, but whose interaction strengths are comparable to those of neutrinos. The most widely-discussed examples arise in the context of supersymmetry (SUSY), which is motivated independently of the dark-matter problem as a theoretical framework for many attempts to unify the forces of nature. SUSY predicts that, for every known fermion in the standard model, there exists a new bosonic "superpartner" and vice versa (more than doubling the number of fundamental degrees of freedom in the simplest models; see [301] for a review). These superpartners were recognized as potential dark-matter candidates in the early 1980s by Cabibbo [302], Pagels and Primack [303], Weinberg [304] and others [305, 306, 307, 308, 309], with the generic term "WIMP" being coined in 1985 [310].

There is, as yet, no firm experimental evidence for SUSY WIMPs. This means that their rest energies, if they exist, lie beyond the range currently probed by accelerators (and in particular beyond the rest energies of their standard-model counterparts). Supersymmetry is, therefore, not an exact symmetry of nature. The masses of the superpartners, like that of the axion (Sec. 6), must have been generated by a symmetry-breaking event in the early Universe. Subsequently, as the temperature of the expanding fireball dropped below their rest energies, heavier species would have dropped out of equilibrium and begun to disappear by pair annihilation, leaving progressively lighter ones behind. Eventually, only one massive superpartner would have remained: the lightest supersymmetric particle (LSP). It is this particle which plays the role of the WIMP in SUSY theories. Calculations using the Boltzmann equation show that the collective density of relic LSPs today lies within one or two orders of magnitude of the required CDM density across much of the parameter space of most SUSY theories [311]. In this respect, SUSY WIMPs are more natural DM candidates than axions (Sec. 6), whose cosmological density ranges a priori over many orders of magnitude.

SUSY WIMPs contribute to the cosmic background radiation in at least three ways. The first is by pair annihilation to photons. This process occurs even in the simplest, or minimal SUSY model (MSSM), but is very slow because it takes place via intermediate loops of charged particles such as leptons and quarks and their antiparticles. The underlying reason for the stability of the LSP in the MSSM is an additional new symmetry of nature, known as R-parity, which is necessary (among other things) to protect the proton from decaying via intermediate SUSY states. The other two types of background contributions occur in non-minimal SUSY theories, in which R-parity is not conserved (and in which the proton can decay). In these theories, LSPs can decay into photons directly via loop diagrams, and also indirectly via tree-level decays to secondary particles which then scatter off pre-existing background photons to produce a signal.

The first step in assessing the importance of each of these processes is to choose an LSP. Early workers variously identified this as the photino (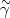) [302], the gravitino (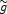) [303], the sneutrino (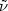) [307] or the selectron (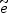) [308]. (SUSY superpartners are denoted by a tilde and take the same names as their standard-model counterparts, with a prefix "s" for superpartners of fermions and a suffix "ino" for those of bosons.) In a landmark study, Ellis [309] showed in 1984 that most of these possibilities are disfavoured, and that the LSP is in fact most likely to be a neutralino (), a linear superposition of the photino (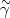), the zino (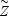) and two neutral higgsinos (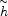₁⁰ and 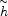₂⁰). (These are the SUSY spin-1/2 counterparts of the photon, Z⁰ and Higgs bosons respectively.) There are four neutralinos, each a mass eigenstate made up of (in general) different amounts of photino, zino, etc., although in special cases a neutralino could be "mostly photino," say, or "pure zino." The LSP is by definition the lightest such eigenstate. Accelerator searches place a lower limit on its rest energy which currently stands at mc² > 46 GeV [312].

In minimal SUSY, the density of neutralinos drops only by way of the (slow) pair-annihilation process, and it is quite possible for these particles to "overclose" the Universe if their rest energy is too high. This does not change the geometry of the Universe, but rather speeds up its expansion rate, which is proportional to the square root of the total matter density from Eq. (22). In such a situation, the Universe would have reached its present size in too short a time. Lower bounds on the age of the Universe thus impose an upper bound on the neutralino rest energy which has been set at m c² 3200 GeV [313]. Detailed exploration of the parameter space of minimal SUSY theory tightens this upper limit in most cases to m c² 600 GeV [314]. Much recent work is focused on a slimmed-down version of the MSSM known as the constrained minimal SUSY model (CMSSM), in which all existing experimental bounds and cosmological requirements are comfortably met by neutralinos with rest energies in the range 90 GeV m c² 400 GeV [315].

Even in its constrained minimal version, SUSY physics contains at least five adjustable input parameters, making the neutralino a considerably harder proposition to test than the axion or the massive neutrino. Fortunately, there are several other ways (besides accelerator searches) to look for these particles. Because their rest energies are above the temperature at which they decoupled from the primordial fireball, WIMPs have non-relativistic velocities and are found predominantly in gravitational potential wells like those of our own Galaxy. They will occasionally scatter against target nuclei in terrestrial detectors as the Earth follows the Sun around the Milky Way. Annual variations in this signal resulting from the Earth's orbital motion through the Galactic dark-matter halo can be used to isolate a WIMP signal. Just such a signal was reported by the DAMA team in 2000 using detectors in Italy's Gran Sasso mountains, with an implied WIMP rest energy of m c² = 52⁺¹⁰_-8 GeV [316]. However, subsequent experiments under the Fréjus peak in France (EDELWEISS [317]) and at Stanford University [318] and the Soudan mine in Minnesota [319] (CDMS) have not been able to reproduce this result. New detectors such as ZEPLIN in England's Boulby mine [320] and IGEX at Canfranc in Spain [321] are rapidly coming online to help with the search.

A second, indirect search strategy is to look for annihilation byproducts from neutralinos which have collected inside massive bodies. Most attention has been directed at the possibility of detecting antiprotons from the Galactic halo [322] or neutrinos from the Sun [323] or Earth [324]. The heat generated in the cores of gas giants like Jupiter or Uranus has also been considered as a potential annihilation signature [325]. The main challenge in each case lies in separating the signal from the background noise. In the case of the Earth, one can look for neutrino-induced muons which are distinguishable from the atmospheric background by the fact that they are travelling straight up. The AMANDA experiment, whose detectors are buried deep in the Antarctic ice, has recently reported upper limits on the density of terrestrial WIMPs based on this principle [326].

8.2. Pair annihilation

Pair annihilation into photons provides a complementary indirect search technique. The photons so produced lie in the -ray portion of the spectrum for the range of WIMP rest energies considered here (50 GeV m c² 1000 GeV). Beginning with Sciama [308], Silk and Srednicki [322], many workers have studied the possibility of -rays from SUSY WIMP annihilations in the halo of the Milky Way, which gives the strongest signal. Prognoses for detection have ranged from very optimistic [327] to very pessimistic [328]; converging gradually to the conclusion that neutralino-annihilation contributions would be at or somewhat below the level of the Galactic background, and possibly distinguishable from it by their spectral shape [329, 330, 331]. Recent studies have focused on possible enhancements of the signal in the presence of a high-density Galactic core [332], a flattened halo [333], a very extended singular halo [334], a massive central black hole [335], significant substructure [336, 337, 338] and adiabatic compression due to baryons [339]. The current state of the art in this area is summarized in Ref. [340] with attention to prospects for detection by the upcoming GLAST mission.

WIMPs at the higher end of the mass range (~ 1 TeV) would produce a weaker signal, but it has been argued that this might be more than made up for by the larger effective area of the atmospheric Cerenkov telescopes (ACTs) used to detect them [342]. Not all authors are as sanguine [343], but new observations of high-energy -rays from the Galactic center by the CANGAROO [344] and VERITAS collaborations [345] provide tantalizing examples of what might be possible with this technique. The Milagro extensive air-shower array is another experiment that has recently set upper limits on the density of ~ TeV WIMPs in the vicinity of the Sun [346]. Other teams have carried the search farther afield, toward objects like dwarf spheroidal galaxies [347], the Large Magellanic Cloud [348] and the giant elliptical galaxy M87 in Virgo [349].

The possibility of neutralino-annihilation contributions to the diffuse extragalactic background, rather than the signal from localized concentrations of dark matter, has received less attention. First to apply the problem to SUSY WIMPs were Cabibbo [302], who however assumed a WIMP rest energy (10-30 eV) which we now know is far too low. Like the decaying neutrino (Sec. 7), this would produce a background in the ultraviolet. It is excluded, however, by an argument due to Lee and Weinberg, which restricts WIMPs to rest energies above 2 GeV [306]. EBL contributions from SUSY WIMPs in this range were first estimated by Silk and Srednicki [322]. Their conclusion, and those of most workers who have followed them [350, 351, 352], is that neutralino annihilations would be responsible for no more than a small fraction of the observed -ray background. Here we review this argument, reversing our usual procedure and attempting to set a reasonably conservative upper limit on neutralino contributions to the EBL.

We concentrate on processes in which neutralino pairs annihilate directly into photon pairs via intermediate loop diagrams (Fig. 32), since these provide the most distinctive signature of new physics. Neutralino annihilations actually produce most of their photons indirectly, via tree-level annihilations to hadrons (mostly pions) which then decay to photons, electrons, positrons and neutrinos. (The electrons and positrons add even more to the signal by inverse Compton scattering off low-energy CMB photons.) However, the energies of the photons produced in this way are broadly distributed, resulting in a continuum -ray spectrum which is difficult if not impossible to distinguish from the astrophysical background [353]. By contrast, the one-loop annihilation processes in Fig. 32 give rise to a photon spectrum that is essentially monoenergetic, E m c² (subject only to modest Doppler broadening due to galactic rotation). No conventional astrophysical processes produce such a narrow peak, whose detection against the diffuse extragalactic background would constitute compelling evidence for dark matter.

Figure 32. Some Feynman diagrams corresponding to the annihilation of two neutralinos (), producing a pair of photons (). The process is mediated by fermions (f) and their supersymmetric counterparts, the sfermions ().

We again take galactic dark-matter halos as our sources of background radiation, with comoving number density n₀. Photon wavelengths are distributed normally about the peak wavelength in the galaxy rest frame:

(221)

where m₁₀ m c² / (10 GeV) is the neutralino rest energy in units of 10 GeV. The standard deviation can be related to the velocity dispersion of bound dark-matter particles as in previous sections, so that = 2(v_c / c) _ann. With v_c ~ 220 km s^-1 and m₁₀ ~ 1 this is of order ~ 10^-9 Å. For convenience we specify this with the dimensionless parameter ₉ / (10^-9 Å). The spectral energy distribution is then given by Eq. (75) as

(222)

The luminosity due to neutralino annihilations is proportional to the rest energy of the annihilating particles times the annihilation rate, which in turn goes as the cross-section (v) times the square of the neutralino number density, n². The resulting expression may be written

(223)

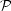
where < v > is the photo-annihilation cross-section (in cm³ s^-1), m^{-2 2}(r) 4 r² dr is the radial average of n² over the halo (in cm^-6) and (r) is the neutralino density distribution (in g cm^-3). Berezinsky [354] have determined < v > a for non-relativistic neutralinos as

(224)

Here is the fine structure constant, m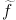 is the mass of an intermediate sfermion, y (Z₁₂ / Z₁₁) tan_W, _W is the weak mixing angle and Z_ij are elements of the real orthogonal matrix which diagonalizes the neutralino mass matrix. In particular, the "pure photino" case is specified by Z₁₁ = sin_W, y = 1 and the "pure zino" by Z₁₁ = cos_W, y = - tan² _W. Collecting these expressions together and parametrizing the sfermion rest energy by 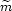₁₀ m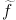 / 10 GeV, we obtain:

(225)

Here f (=1 for photinos, 0.4 for zinos) is a dimensionless quantity whose value parametrizes the makeup of the neutralino.

Since we attempt in this section to set an upper limit on EBL contributions from neutralino annihilations, we take f 1 (the photino case). In the same spirit, we would like to use lower limits for the sfermion mass 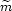₁₀. It is important to estimate this quantity accurately since the cross-section goes as 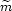₁₀^-4. Giudice and Griest [355] have made a detailed study of photino annihilations and find a lower limit on 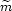₁₀ as a function of m₁₀, assuming that photinos provide at least 0.025h₀^-2 of the critical density. Over the range 0.1 m₁₀ 4, this lower limit is empirically well fit by a function of the form 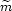₁₀ 4m₁₀ ^0.3. If this holds over our broader range of masses, then we obtain an upper limit on the neutralino annihilation cross-section of < v > (3 × 10^-29 cm³s^-1) m₁₀^0.8. This expression gives results which are about an order of magnitude higher than the cross-sections quoted by Gao [351].

For the WIMP density distribution (r) we adopt the simple and widely-used isothermal model [331]:

(226)

Here = 5 × 10^-25 g cm^-3 is the approximate dark-matter density in the solar vicinity, assuming a spherical halo [260], r = 8 kpc is the distance of the Sun from the Galactic center [356] and a = (2 - 20) kpc is a core radius. To fix this latter parameter, we can integrate (226) over volume to obtain total halo mass M_h(r) inside radius r:

(227)

Observations of the motions of Galactic satellites imply that the total mass inside 50 kpc is about 5 × 10¹¹ M [75]. This in (227) implies a = 9 kpc, which we consequently adopt. The maximum extent of the halo is not well-constrained observationally, but can be specified if we take M_h = (2 ± 1) × 10¹² M as in (175). Eq. (227) then gives a halo radius r_h = (170 ± 80) kpc. The cosmological density of WIMPs in galactic dark-matter halos adds up to _h = n₀ M_h / _crit,0 = (0.07 ± 0.04) h₀.

If there are no other sources of CDM, then the total matter density is _m,0 = _h + _bar 0.1h₀ and the observed flatness of the Universe (Sec. 4) implies a strongly vacuum-dominated cosmology. While we use this as a lower limit on WIMP contributions to the dark matter in subsequent sections, it is quite possible that CDM also exists in larger-scale regions such as galaxy clusters. To take this into account in a general way, we define a cosmological enhancement factor f_c (_m,0 - _bar) / _h representing the added contributions from WIMPs outside galactic halos (or perhaps in halos which extend far enough to fill the space between galaxies). This takes the value f_c = 1 for the most conservative case just described, but rises to f_c = (4 ± 2) h₀^-1 in the CDM model with _m,0 = 0.3, and (14 ± 7) h₀^-1 in the EdS model with _m,0 = 1.

With (r) known, we are in a position to calculate the quantity :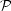

(228)

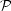
Using the values for , r and a specified above and setting r_h = 250 kpc to get an upper limit, we find that (5 × 10⁶⁵ cm^-3) m₁₀^-2. Putting this result along with the cross-section (225) into (223), we obtain:

(229)

Inserting Giudice and Griest's [355] lower limit on the sfermion mass 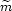₁₀ (as empirically fit above), we find that (229) gives an upper limit on halo luminosity of L_h,ann (5 × 10³⁵ erg s^-1) f m₁₀^-0.2. Higher estimates can be found in the literature [357], but these assume a singular halo whose density drops off as only (r) r^-1.8 and extends out to a very large halo radius, r_h = 4.2 h₀^-1 Mpc. For a standard isothermal distribution of the form (226), our results confirm that halo luminosity due to neutralino annihilations alone is very low, amounting to less than 10^-8 times the total bolometric luminosity of the Milky Way.

The combined bolometric intensity of neutralino annihilations between redshift z_f and the present is given by substituting the comoving number density n₀ and luminosity L_h,ann into Eq. (15) to give

(230)

where Q_,ann = (cn₀ L_h,annf_c) / H₀ and we have assumed spatial flatness. With values for all these parameters as specified above, we find

(231)

Here we have set z_f = 30 (larger values do not substantially increase the value of Q) and used values of f_c = 1, 4h₀^-1 and 20h₀^-1 respectively. The effects of a larger cosmological enhancement factor f_c are partially offset in (230) by the fact that a universe with higher matter density _m,0 is younger, and hence contains less background light in general. Even the highest value of Q given in (231) is negligible in comparison to the intensity (21) of the EBL due to ordinary galaxies.

The total spectral intensity of annihilating neutralinos is found by substituting the SED (222) into (62) to give

(232)

For a typical neutralino with m₁₀ 10 the annihilation spectrum peaks near ₀ 10^-7 Å. The dimensional prefactor reads

			(233)

Here we have divided through by the photon energy hc / ₀ to put results into continuum units or CUs as usual (Sec. 3.2). Eq. (232) gives the combined intensity of radiation from neutralino annihilations, emitted at various wavelengths and redshifted by various amounts, but observed at wavelength ₀. Results are plotted in Fig. 33 together with observational constraints.

Figure 33. The spectral intensity of the diffuse -ray background due to neutralino annihilations (lower left), compared with observational limits from high-altitude balloon experiments (N80), the SAS-2 spacecraft and the COMPTEL and EGRET instruments. The three plotted curves for each value of m c2 depend on the total density of neutralinos: galaxy halos only (m,0 = 0.1h0; heavy lines), CDM model (m,0 = 0.3; medium lines), or EdS model (m,0 = 1; light lines).

8.3. One-loop decays

We turn next to non-minimal SUSY theories in which R-parity is not necessarily conserved and the LSP (in this case the neutralino) can decay. The cosmological consequences of R-parity breaking have been reviewed by Bouquet and Salati [358]. There is one direct decay mode into photons, + . Feynman diagrams for this process are shown in Fig. 34. Because these decays occur via loop diagrams, they are again subdominant. We consider theories in which R-parity breaking is accomplished spontaneously. 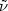This means introducing a scalar sneutrino with a nonzero vacuum expectation value v_R < _R >, as discussed by Masiero and Valle [359]. Neutralino decays into photons could be detectable if m and v_R are large [360].

Figure 34. Some Feynman diagrams corresponding to one-loop decays of the neutralino () into a neutrino (here the -neutrino and a photon (). The process can be mediated by the W-boson and a -lepton, or by the and its supersymmetric counterpart ().

The photons produced in this way are again monochromatic, with E = 1/2 m c². In fact the SED here is the same as (222) except that peak wavelength is doubled, _loop = 2hc / m c² = (2.5 × 10^-6 Å) m₁₀^-1. The only parameter that needs to be recalculated is the halo luminosity L_h. For one-loop neutralino decays of lifetime , this takes the form:

(234)

Here N = M_h / m is the number of neutralinos in the halo and b is the branching ratio, or fraction of neutralinos that decay into photons. This is estimated by Berezinsky [360] as

(235)

where the new parameter f_R v_R / (100 GeV). The requirement that SUSY WIMPs not carry too much energy out of stellar cores implies that f_R is of order ten or more [359]. We take f_R > 1 as a lower limit.

We adopt M_h = (2 ± 1) × 10¹² M as usual, with r_h = (170 ± 80) kpc from the discussion following (227). As in the previous section, we parametrize our lack of certainty about the distribution of neutralinos on larger scales with the cosmological enhancement factor f_c. Collecting these results together and expressing the decay lifetime in dimensionless form as f / (1 Gyr), we obtain for the luminosity of one-loop neutralino decays in the halo:

(236)

With m₁₀ ~ f_R ~ f ~ 1, Eq. (236) gives L_h,loop ~ 2 × 10⁷ L. This is considerably brighter than the halo luminosity due to neutralino annihilations in minimal SUSY models, but still amounts to less than 10^-3 times the bolometric luminosity of the Milky Way.

Combined bolometric intensity is found as in the previous section, but with L_h,ann in (230) replaced by L_h,loop so that

(237)

This is again small. However, we see that massive (m₁₀ 10) neutralinos which provide close to the critical density (_m,0 ~ 1) and decay on timescales of order 1 Gyr or less (f 1) could in principle rival the intensity of the conventional EBL.

To obtain more quantitative constraints, we turn to spectral intensity. This is given by Eq. (232) as before, except that the dimensional prefactor I_,ann must be replaced by

			(238)

Results are plotted in Fig. 35 for neutralino rest energies 1 m₁₀ 100. While their bolometric intensity is low, these particles are capable of significant EBL contributions in narrow portions of the -ray background. To keep the diagram from becoming too cluttered, we have assumed values of f such that the highest predicted intensity in each case stays just below the EGRET limits. Numerically, this corresponds to lower bounds on the decay lifetime of between 100 Gyr (for m c² = 10 GeV) and 10⁵ Gyr (for m c² = 300 GeV). For rest energies at the upper end of this range, these limits are probably optimistic because the decay photons are energetic enough to undergo pair production on CMB photons. Some would not reach us from cosmological distances, instead being re-processed into lower energies along the way. As we show in the next section, however, stronger limits arise from a different process in any case. We defer further discussion of Fig. 35 to Sec. 8.6.

Figure 35. The spectral intensity of the diffuse -ray background due to neutralino one-loop decays (lower left), compared with observational upper limits from high-altitude balloon experiments (filled dots), SAS-2, EGRET and COMPTEL. The three plotted curves for each value of m c2 correspond to models with m,0 = 0.1h0 (heavy lines), m,0 = 0.3 (medium lines) and m,0 = 1 (light lines). For clarity we have assumed decay lifetimes in each case such that highest theoretical intensities lie just under the observational constraints.

8.4. Tree-level decays

The dominant decay processes for the LSP neutralino in non-minimal SUSY (assuming spontaneously broken R-parity) are tree-level decays to leptons and neutrinos, ⁺ + ^- + . Of particular interest is the case = e; Feynman diagrams for this process are shown in Fig. 36. Although these processes do not contribute directly to the EBL, they do so indirectly, because the high-energy electrons undergo inverse Compton scattering (ICS) off the CMB photons via e + _cmb e + . This gives rise to a flux of high-energy photons which can be at least as important as those from the direct (one-loop) neutralino decays considered in the previous subsection [361].

Figure 36. The Feynman diagrams corresponding to tree-level decays of the neutralino () into a neutrino () and a lepton-antilepton pair (here, the electron and positron). The process can be mediated by the W or Z-boson.

The spectrum of photons produced in this way depends on the rest energy of the original neutralino. We consider first the case m₁₀ 10, which is more or less pure ICS. The input ("zero-generation") electrons are monoenergetic, but after multiple scatterings they are distributed like E^-2 [362]. From this the spectrum of outgoing photons can be calculated as [363]

(239)

where

Here E_e = 1/3 m c² = (3.3 GeV) m₁₀ is the energy of the input electrons, m_e is their rest mass, and E_cmb = 2.7kT_cmb is the mean energy of the CMB photons. Using m_e c² = 0.51 MeV and T_cmb = 2.7 K, and allowing for decays at arbitrary redshift z (after Berezinsky [363]), we obtain the expression E_max(z) = (36 keV) m₁₀²(1 + z)^-1.

The halo SED may be determined as a function of wavelength by setting F() d = EN(E) dE where E = hc / . Normalizing the spectrum so that ₀ F() d = L_h,tree, we find:

(240)

where = hc / E_max = (0.34 Å) m₁₀^-2(1 + z) and L_h,tree is the halo luminosity due to tree-level decays.

In the case of more massive neutralinos with m₁₀ 10, the situation is complicated by the fact that outgoing photons become energetic enough to initiate pair production via + _cmb e⁺ + e^-. This injects new electrons into the ICS process, resulting in electromagnetic cascades. For particles which decay at high redshifts (z 100), other processes such as photon-photon scattering must also be taken into account [364]. Cascades on non-CMB background photons may also be important [365]. A full treatment of these effects requires detailed numerical analysis [366]. Here we simplify the problem by assuming that the LSP is stable enough to survive into the late matter-dominated (or vacuum-dominated) era. The primary effect of cascades is to steepen the decay spectrum at high energies, so that [363]

(241)

where

Here E₀ is a minimum absorption energy. We adopt the numerical expressions E_x = (1.8 × 10³ GeV)(1 + z)^-1 and E_c = (4.5 × 10⁴ GeV)(1 + z)^-1 after Protheroe [367]. Employing the relation F() d = EN(E) dE and normalizing as before, we find:

(242)

where the new parameters are _x = hc / E_x = (7 × 10^-9 Å)(1 + z) and _c = hc / E_c = (3 × 10^-10 Å)(1 + z).

The luminosity L_h,tree is given by

(243)

where b_e is now the branching ratio for all processes of the form e + all and E_e = 2/3 m c² is the total energy lost to the electrons. We assume that all of this eventually finds its way into the EBL. Berezinsky [360] supply the following branching ratio:

(244)

Here f parametrizes the composition of the neutralino, taking the value 0.4 for the pure higgsino case. With the halo mass specified by (175) and f / (1 Gyr) as usual, we obtain:

(245)

This is approximately four orders of magnitude higher than the halo luminosity due to one-loop decays, and provides for the first time the possibility of significant EBL contributions. With all adjustable parameters taking values of order unity, we find that L_h,tree ~ 2 × 10¹⁰ L, which is comparable to the bolometric luminosity of the Milky Way.

The combined bolometric intensity of all neutralino halos is computed as in the previous two sections. Replacing L_h,loop in (230) with L_h,tree leads to

(246)

These are of the same order as (or higher than) the bolometric intensity of the EBL from ordinary galaxies, Eq. (21).

To obtain the spectral intensity, we substitute the SEDs F_ics() and F_casc() into Eq. (62). The results can be written

(247)

where the quantities I_,tree and (z) are defined as follows. For neutralino rest energies m₁₀ 10 (ICS):

			(248)

Conversely, for m₁₀ 10 (cascades):

			(249)

Numerical integration of Eq. (247) leads to the plots in Fig. 37. Cascades (like the pair annihilations we have considered already) dominate the -ray part of the spectrum. The ICS process, however, is most important at lower energies, in the x-ray region. We discuss the observational limits and the constraints that can be drawn from them in more detail in Sec. 8.6.

Figure 37. The spectral intensity of the diffuse -ray and x-ray backgrounds due to neutralino tree-level decays, compared with observational upper limits from SAS-2, EGRET and COMPTEL in the -ray region, from XMM-Newton and RXTE in the x-ray region, and from Gruber's fits to various experimental data (G92,G99). The three plotted curves for each value of m c2 correspond to models with m,0 = 0.1h0 (heavy lines), m,0 = 0.3 (medium lines) and m,0 = 1 (light lines). For clarity we have assumed decay lifetimes in each case such that highest theoretical intensities lie just under the observational constraints.

8.5. Gravitinos

Gravitinos (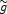) are the SUSY spin-3/2 counterparts of gravitons. Although often mentioned along with neutralinos, they are not favoured as dark-matter candidates in the simplest SUSY theories. The reason for this, known as the gravitino problem [305], boils down to the fact that they interact too weakly, not only with other particles but with themselves as well. Hence they annihilate slowly and survive long enough to "overclose" the Universe unless some other way is found to reduce their numbers. Decays are one possibility, but not if the gravitino is a stable LSP. Gravitino decay products must also not be allowed to interfere with processes such as primordial nucleosynthesis [304]. Inflation, followed by a judicious period of reheating, can thin out their numbers to almost any desired level. But the reheat temperature T_R must satisfy kT_R 10¹² GeV or gravitinos will once again become too numerous [309]. Related arguments based on entropy production, primordial nucleosynthesis and the CMB power spectrum force this number down to kT_R (10⁹ - 10¹⁰) GeV [368] or even kT_R (10⁶ - 10⁹) GeV [369]. These temperatures are incompatible with the generation of baryon asymmetry in the Universe, a process which is usually taken to require kT_R ~ 10¹⁴ GeV or higher [96].

Recent developments are however beginning to loosen the baryogenesis requirement [370], and there are alternative models in which baryon asymmetry is generated at energies as low as ~ 10 TeV [371] or even 10 MeV - 1 GeV [372]. With this in mind we include a brief look at gravitinos here. There are two possibilities: (1) If the gravitino is not the LSP, then it decays early in the history of the Universe, well before the onset of the matter-dominated era. 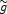In models where the gravitino decays both radiatively and hadronically, for example, it can be "long-lived for its mass" with a lifetime of 10⁶ s [373]. Particles of this kind have important consequences for nucleosynthesis, and might affect the shape of the CMB if 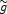were to exceed ~ 10⁷ s. However, they are irrelevant as far as the EBL is concerned. We therefore restrict our attention to the case (2), in which the gravitino is the LSP. In light of the results we have already obtained for the neutralino, we disregard annihilations and consider only models in which the LSP can decay.

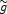
The decay mode depends on the specific mechanism of R-parity violation. We follow Berezinsky [374] and concentrate on dominant tree-level processes. In particular we consider the decay e⁺ + all , followed by ICS off the CMB, as in Sec. 8.4. 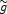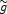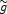The spectrum of photons produced by this process is identical to that in the neutralino case, except that the mono-energetic electrons have energy E_e = 1/2 m c² = (5 GeV) m₁₀ [374], where m c² is the rest energy of the gravitino and m₁₀ m c² / (10 GeV) as before. This in turn implies that E_max = (81 keV) m₁₀²(1 + z)^-1 and = hc / E_max = (0.15 Å) m₁₀^-2(1 + z). The values of _x and _c are unchanged.

The SED comprises Eqs. (240) for ICS and (242) for cascades, as before. Only the halo luminosity needs to be recalculated. This is similar to Eq. (243) for neutralinos, except that the factor of 2/3 becomes 1/2, and the branching ratio can be estimated at [374]

(250)

Using our standard value for the halo mass M_h, and parametrizing the gravitino decay lifetime by f 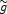/ (1 Gyr) as before, we obtain the following halo luminosity due to gravitino decays:

(251)

This is higher than the luminosity due to neutralino decays, and exceeds the luminosity of the Milky Way by several times if f ~ 1.

The bolometric intensity of all gravitino halos is computed exactly as before. Replacing L_h,tree in (230) with L_h,grav, we find:

(252)

It is clear that gravitinos must decay on timescales longer than the lifetime of the Universe (f 16), or they would produce a background brighter than that of the galaxies.

The spectral intensity is the same as before, Eq. (247), but with the new numbers for and L_h. This results in

(253)

where the prefactor I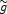 is defined as follows. For m₁₀ 10 (ICS):

			(254)

Conversely, for m₁₀ 10 (cascades):

			(255)

The function (z) has the same form as in Eqs. (248) and (249) and does not need to be redefined (requiring only the new value for the cutoff wavelength ). Because the branching ratio b_e in (250) is independent of the gravitino rest mass, m₁₀ appears in these results only through . Thus the ICS part of the spectrum goes as m₁₀^-1 while the cascade part does not depend on m₁₀ at all. As with neutralinos, cascades dominate the -ray part of the spectrum, and the ICS process is most important in the x-ray region. Numerical integration of Eq. (253) leads to the results plotted in Fig. 38. We proceed in the next section to discuss these, comparing them to our previous results for neutralinos, and beginning with an overview of the observational constraints.

Figure 38. The spectral intensity of the diffuse -ray and x-ray backgrounds due to gravitino tree-level decays, compared with experimental data from SAS-2, EGRET, COMPTEL, XMM-Newton and RXTE, as well as compilations by Gruber. The three plotted curves for each value of m c2 correspond to models with m,0 = 0.1h0 (heavy lines), m,0 = 0.3 (medium lines) and m,0 = 1 (light lines). For clarity we have assumed decay lifetimes in each case such that highest theoretical intensities lie just under the observational constraints.

8.6. The x-ray and -ray backgrounds

The experimental situation as regards EBL intensity in the x-ray and -ray regions is more settled than that in the optical and ultraviolet. Detections (as opposed to upper limits) have been made in both bands, and are consistent with expectations based on known astrophysical sources. The constraints that we derive here are thus conservative ones, in the sense that the EBL flux which could plausibly be due to decaying WIMPs is almost certainly smaller than the levels actually measured.

At the lowest or soft x-ray energies, which lie roughly between 0.1-3 keV (4-100 Å), new measurements have been reported from the Chandra spacecraft [375]. (Universal conventions have not been established regarding the boundaries between different wavebands; we follow most authors and define these according to the different detection techniques that must be used in each region.) These data appear as a small bowtie-shaped box near ₀ ~ 10 Å in Fig. 1, where it can be seen that they interpolate beautifully between previous detections at shorter and longer wavelengths. The small rectangle immediately to the right of the Chandra bowtie (near ₀ ~ 100 Å) in Fig. 1 comes from measurements by the EUVE satellite in 1993 [376].

The hard x-ray background (3-800 keV, or 0.02-4 Å) is crucial in constraining the decays of low-mass neutralinos and gravitinos via the ICS process, as can be seen in Figs. 37 and 38. We have plotted two compilations of observational data in the hard x-ray band, both by Gruber [377, 378]. The first (labelled "G92" in Figs. 37 and 38) is an empirical fit to various pre-1992 measurements, including those from the Kosmos and Apollo spacecraft, HEAO-1 and balloon experiments. The range of uncertainty in this data increases logarithmically from 2% at 3 keV to 60% at 3 MeV [377]. The second compilation (labelled "G99") is a revision of this fit in light of new data at higher energies, and has been extended deep into the -ray region. New results from XMM-Newton [379] and the Rossi X-ray Timing Explorer [380] confirm the accuracy of this revised fit at low energies ("L02" and "R03" respectively in Figs. 37 and 38). The prominent peak in the range 3-300 keV (0.04-4 Å) is widely attributed to integrated light from active galactic nuclei (AGN) [381].

In the low-energy -ray region (0.8-30 MeV, or 0.0004-0.02 Å) we have used results from the COMPTEL instrument on the Compton Gamma-Ray Observatory (CGRO), which was operational from 1990-2000 [382]. Four data points are plotted in Figs. 33, 35, 37 and 38, and two more (upper limits only) appear at low energies in Figs. 37 and 38. These experimental results, which interpolate smoothly between other data at both lower and higher energies, played a key role in the demise of the "MeV bump" (visible in Figs. 37 and 38 as a significant upturn in Gruber's fit to the pre-1992 data from about 0.002-0.02 Å). This apparent feature in the background had attracted a great deal of attention from theoretical cosmologists as a possible signature of new physics. Figs. 37 and 38 suggest that it could also have been interpreted as the signature of a long-lived non-minimal SUSY WIMP with a rest energy near 100 GeV. The MeV bump is, however, no longer believed to be real, as the new fit ("G99") makes clear. Most of the background in this region is now suspected to be due to Type Ia supernovae (SNIa) [383].

We have included two measurements in the high-energy -ray band (30 MeV-30 GeV, or 4 × 10^-7 - 4 × 10^-4 Å): one from the SAS-2 satellite which flew in 1972-3 [384] and one from the EGRET instrument which was part of the CGRO mission along with COMPTEL [385]. As may be seen in Figs. 33, 35, 37 and 38, the new results essentially extend the old ones to 120 GeV (₀ = 10^-7 Å), with error bars which have been reduced by a factor of about ten. Most of this extragalactic background is thought to arise from unresolved blazars, highly variable AGN whose relativistic jets point in our direction [386]. Some authors have recently argued that Galactic contributions to the background were underestimated in the original EGRET analysis [387, 388]; if so, the true extragalactic background intensity would be lower than that plotted here, strengthening the constraints we derive below.

Because the extragalactic component of the -ray background has not been reliably detected beyond 120 GeV, we have fallen back on measurements of total flux in the very high-energy (VHE) region (30 GeV-30 TeV, or 4 × 10^-10 - 4 × 10^-7 Å). These were obtained from a series of balloon experiments by Nishimura in 1980 [389], and appear in Figs. 33 and 35 as filled dots (labelled "N80"). They constitute a very robust upper limit on EBL flux, since much of this signal must have originated in the upper atmosphere. At the very highest energies, in the ultra high-energy (UHE) region (> 30 TeV), these data join smoothly to upper limits on the diffuse -ray flux from extensive air-shower arrays such as HEGRA (20-100 TeV [390]) and CASA-MIA (330 TeV-33 PeV [391]). Here we reach the edge of the EBL for practical purposes, since -rays with energies of ~ 10 - 100 PeV are attenuated by pair production on CMB photons over scales ~ 30 kpc [392].

Some comments are in order here about units. For experimental reasons, measurements of x-ray and -ray backgrounds are often expressed in terms of integral flux EI_E( > E₀), or number of photons with energies above E₀. This presents no difficulties since the differential spectrum in this region is well approximated with a single power-law component, I_E(E₀) = I_*(E₀ / E_*)^-. The conversion to integral form is then given by

(256)

The spectrum is specified in either case by its index together with the values of E_* and I_* (or E₀ and EI_E in the integral case). Thus SAS-2 results were reported as = 2.35^+0.4_-0.3 with EI_E = (5.5 ± 1.3) × 10^-5 s^-1 cm^-2 ster^-1 for E₀ = 100 MeV [384]. The EGRET spectrum is instead fit by = 2.10 ± 0.03 with I_* = (7.32 ± 0.34) × 10^-9 s^-1 cm^-2 ster^-1 MeV^-1 for E_* = 451 MeV [385]. To convert a differential flux in these units to I in CUs, one multiplies by E₀/₀ = E₀² / hc = 80.66E₀² where E₀ is photon energy in MeV.

We now discuss our results, beginning with the neutralino annihilation fluxes plotted in Fig. 33. These are at least four orders of magnitude fainter than the background detected by EGRET [385] (and five orders of magnitude below the upper limit set by the data of Nishimura [389] at shorter wavelengths). This agrees with previous studies assuming a critical density of neutralinos [322, 351]. Fig. 33 shows that EBL contributions would drop by another order of magnitude in the favoured scenario with _m,0 0.3, and by another if neutralinos are confined to galaxy halos (_m,0 0.1h₀). Because the annihilation rate goes as the square of the WIMP density, it has been argued that modelling WIMP halos with steep density cusps might raise their luminosity, possibly enhancing their EBL contributions by a factor of as much as ~ 10⁴ -10⁵ [393]. While such a scenario might in principle bring WIMP annihilations back up to the brink of observability in the diffuse background, density profiles with the required steepness are not seen in either our own Galaxy or those nearby. More recent assessments have reconfirmed the general outlook discussed above in Sec. 8.2; namely, that the best place to look for WIMP annihilations is in the direction of nearby concentrations of dark matter such as the Galactic center and dwarf spheroidals in the Local Group [340, 341]. The same stability that makes minimal-SUSY WIMPs so compelling as dark-matter candidates also makes them hard to detect.

Fig. 35 shows the EBL contributions from one-loop neutralino decays in non-minimal SUSY. We have put h₀ = 0.75, z_f = 30 and f_R = 1. Depending on their decay lifetime (here parametrized by f), these particles are capable in principle of producing a backgound comparable to (or even in excess of) the EGRET limits. The plots in Fig. 35 correspond to the smallest values of f that are consistent with the data for m₁₀ = 1, 3, 10, 30 and 100. Following the same procedure here as we did for axions in Sec. 6, we can repeat this calculation over more finely-spaced intervals in neutralino rest mass, obtaining a lower limit on decay lifetime as a function of m. Results are shown in Fig. 39 (dotted lines). The lower limit obtained in this way varies from 4 Gyr for the lightest neutralinos (assumed to be confined to galaxy halos with a total matter density of _m,0 = 0.1h₀) to 70,000 Gyr for the heaviest (which provide enough CDM to put _m,0 = 1).

Figure 39. The lower limits on WIMP decay lifetime derived from observations of the x-ray and -ray backgrounds. Neutralino bounds are shown for both one-loop decays (dotted lines) and tree-level decays (dashed lines). For gravitinos we show only the tree-level constraints (solid lines). For each process there are three curves corresponding to models with m,0 = 1 (light lines), m,0 = 0.3 (medium lines) and m,0 = 0.1h0 (heavy lines).

Fig. 37 is a plot of EBL flux from indirect neutralino decays via the tree-level, ICS and cascade processes described in Sec. 8.4. These provide us with our strongest constraints on non-minimal SUSY WIMPs. We have set h₀ = 0.75, z_f = 30 and f = f_R = 1, and assumed values of f such that the highest predicted intensities lie just under observational limits, as before. Neutralinos at the light end of the mass range are constrained by x-ray data, while those at the heavy end run up against the EGRET measurements. Both the shape and absolute intensity of the ICS spectra depend on the neutralino rest mass, but the cascade spectra depend on m₁₀ through intensity alone (via the prefactor I_,tree). When normalized to the observational upper bound, all curves for m₁₀ > 10 therefore overlap. Normalizing across the full range of neutralino rest masses (as for one-loop decays) gives the lower bound on lifetime plotted in Fig. 39 (dashed lines). This varies from 60 Gyr to 6 × 10⁷ Gyr, depending on the values of m c² and _m,0.

Fig. 38, finally, shows the EBL contributions from tree-level gravitino decays. These follow the same pattern as the neutralino decays. Requiring that the predicted signal not exceed the x-ray and -ray observations, we obtain the lower limits on decay lifetime plotted in Fig. 39 (solid lines). The flatness of these curves (relative to the constraints on neutralinos) is a consequence of the fact that the branching ratio (250) is independent of m₁₀. Our lower limits on range from 200 Gyr to 20, 000 Gyr.

Let us sum up our findings in this section. We have considered neutralinos and gravitinos, either of which could be the LSP and hence make up the dark matter. In the context of non-minimal SUSY theories, these particles can decay and contribute to both the x-ray and -ray backgrounds. We have shown that any such decay must occur on timescales longer than 10² - 10⁸ Gyr (for neutralinos) or 10² - 10⁴ Gyr (for gravitinos), depending on their rest masses and various theoretical input parameters. These results confirm that, whether it is a neutralino or gravitino, the LSP in non-minimal SUSY theories must be very nearly stable . To the extent that an "almost-stable" LSP would require that R-party conservation be violated at improbably low levels, our constraints suggest that the SUSY WIMP either exists in the context of minimal SUSY theories, or not at all.