


Let us next consider some key events in the evolutionary history of our
universe
[8].
The most well understood phase of the universe occurs when the
temperature is less than about 1012 K. Above this
temperature, thermal production of baryons and
their strong interaction is significant and somewhat difficult to
model. We can ignore
such complications at lower temperatures and - as we shall see -
several interesting
physical phenomena did take place during the later epochs with
T  1012.
1012.
The first thing we need to do is to determine the composition of the
universe when
T  1012 K. We will certainly have, at this time, copious
amount of photons and all species of neutrinos and antineutrinos. In
addition, neutrons and protons must exist
at this time since there is no way they could be produced later
on. (This implies that phenomena which took place at higher temperatures
should have left a small excess of
baryons over anti baryons; we do not quite understand how this happened
and will just take it as an initial condition.)
Since the rest mass of electrons correspond to a much lower temperature
(about 0.5 × 1010 K),
there will be large number of electrons and positrons at this
temperature but in order to maintain
charge neutrality, we need to have a slight excess of electrons over
positrons (by about 1 part
in 109) with the net negative charge compensating the
positive charge contributed by protons.
1012 K. We will certainly have, at this time, copious
amount of photons and all species of neutrinos and antineutrinos. In
addition, neutrons and protons must exist
at this time since there is no way they could be produced later
on. (This implies that phenomena which took place at higher temperatures
should have left a small excess of
baryons over anti baryons; we do not quite understand how this happened
and will just take it as an initial condition.)
Since the rest mass of electrons correspond to a much lower temperature
(about 0.5 × 1010 K),
there will be large number of electrons and positrons at this
temperature but in order to maintain
charge neutrality, we need to have a slight excess of electrons over
positrons (by about 1 part
in 109) with the net negative charge compensating the
positive charge contributed by protons.
An elementary calculation using the known interaction rates show that
all these particles are in thermal equilibrium at this epoch. Hence
standard rules of
statistical mechanics allows us to determine the number density (n),
energy density
( ) and
the pressure (p) in terms of the distribution function f:
) and
the pressure (p) in terms of the distribution function f:
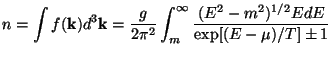 |
(10) |
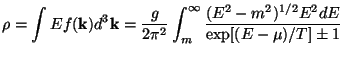 |
(11) |
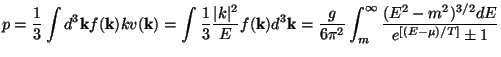 |
(12) |
Next, we can argue that the chemical potentials for electrons, positrons
and neutrinos can be taken to be
zero. For example, conservation of chemical potential in the reaction
e+e-
 2
2  implies that
the chemical potentials of electrons and positrons must differ in a
sign. But since the number densities of electrons and positrons, which
are determined by the chemical potential, are very close to each other,
the chemical potentials of electrons and positrons must be (very
closely) equal to each other. Hence both must be (very close to)
zero. Similar reasoning based on lepton number shows that neutrinos
should also have zero chemical potential. Given this, one can evaluate
the integrals for all the relativistic
species and we obtain for the total energy density
implies that
the chemical potentials of electrons and positrons must differ in a
sign. But since the number densities of electrons and positrons, which
are determined by the chemical potential, are very close to each other,
the chemical potentials of electrons and positrons must be (very
closely) equal to each other. Hence both must be (very close to)
zero. Similar reasoning based on lepton number shows that neutrinos
should also have zero chemical potential. Given this, one can evaluate
the integrals for all the relativistic
species and we obtain for the total energy density
 |
(13) |
where
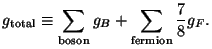 |
(14) |
The corresponding entropy density is given by
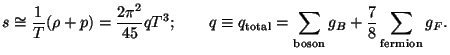 |
(15) |
As a simple application of the above result, let us consider the fate of
neutrinos in the expanding universe. From the standard weak interaction
theory, one can compute the reaction rate
 of the
neutrinos with the rest of the species. When this
reaction rate fall below the expansion rate H of the universe,
the reactions cannot keep the neutrinos coupled to the rest of the
matter. A simple calculation
[8]
shows that the relevant ratio is given by
of the
neutrinos with the rest of the species. When this
reaction rate fall below the expansion rate H of the universe,
the reactions cannot keep the neutrinos coupled to the rest of the
matter. A simple calculation
[8]
shows that the relevant ratio is given by
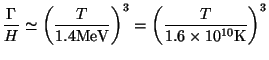 |
(16) |
Thus, for T  1.6 × 1010 K, the neutrinos decouple from matter. At
slightly lower temperature, the electrons and positrons annihilate
increasing the number density of photons. Neutrinos do not get any
share of this energy since they have already decoupled from the rest of
the matter. As a result, the photon temperature goes up with respect to
the neutrino temperature once the
e+e- annihilation is complete. This
increase in the temperature
is easy to calculate. As far as the photons are concerned, the increase
in the temperature is essentially due to the change in the degrees of
freedom g and is given by:
1.6 × 1010 K, the neutrinos decouple from matter. At
slightly lower temperature, the electrons and positrons annihilate
increasing the number density of photons. Neutrinos do not get any
share of this energy since they have already decoupled from the rest of
the matter. As a result, the photon temperature goes up with respect to
the neutrino temperature once the
e+e- annihilation is complete. This
increase in the temperature
is easy to calculate. As far as the photons are concerned, the increase
in the temperature is essentially due to the change in the degrees of
freedom g and is given by:
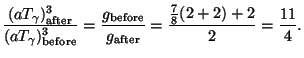 |
(17) |
(In the numerator, one 2 is for electron; one 2 is for positron; the 7/8 factor arises because these are fermions. The final 2 is for photons. In the denominator, there are only photons to take care of.) Therefore
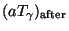 |
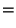 |
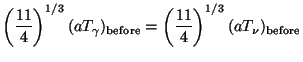 |
|
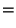 |
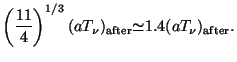 |
(18) |
The first equality is from Eq. (17); the second arises because the
photons and neutrinos had the same temperature originally; the third
equality is from the fact that for decoupled neutrinos
aT is a constant. This result leads to the prediction that, at present, the
universe will contain a bath of neutrinos which has temperature that is
(predictably) lower than that of CMBR. The future detection of such a
cosmic neutrino background will allow us to probe the universe at its
earliest epochs.
is a constant. This result leads to the prediction that, at present, the
universe will contain a bath of neutrinos which has temperature that is
(predictably) lower than that of CMBR. The future detection of such a
cosmic neutrino background will allow us to probe the universe at its
earliest epochs.
2.2. Primordial Nucleosynthesis
When the temperature of the universe is higher than the binding
energy of the nuclei (~ MeV), none of the heavy elements (helium and the
metals) could have existed in the universe.
The binding energies of the first four light nuclei,
2H, 3H, 3He
and 4He are 2.22 MeV, 6.92 MeV,
7.72 MeV and 28.3 MeV respectively.
This would suggest that these nuclei could be
formed when the temperature of the universe is in the range of
(1 - 30)MeV. The actual synthesis takes place only at a much lower
temperature, Tnuc = Tn
 0.1MeV. The main reason
for this delay is the `high entropy' of our universe, i.e., the high
value for the photon-to-baryon ratio,
0.1MeV. The main reason
for this delay is the `high entropy' of our universe, i.e., the high
value for the photon-to-baryon ratio,
 -1.
Numerically,
-1.
Numerically,
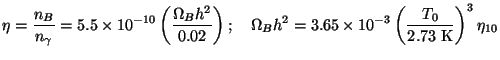 |
(19) |
To see this, let us assume, for a moment, that the nuclear (and other) reactions are fast enough to maintain thermal equilibrium between various species of particles and nuclei. In thermal equilibrium, the number density of a nuclear species a NZ with atomic mass A and charge Z will be
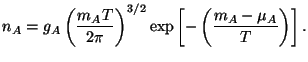 |
(20) |
From this one can obtain the equation
for the temperature TA at which the mass
fraction of a particular species-A will be of order unity
(XA
 1). We find that
1). We find that
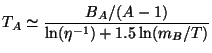 |
(21) |
where BA is the binding energy of the species.
This temperature will be fairly lower than BA
because of the large value of
 -1.
For 2H, 3He and
4He the value of TA is 0.07 MeV,
0.11 MeV and 0.28 MeV respectively. Comparison
with the binding energy of these nuclei shows that these values are
lower than the corresponding binding energies BA
by a factor of about 10, at least.
-1.
For 2H, 3He and
4He the value of TA is 0.07 MeV,
0.11 MeV and 0.28 MeV respectively. Comparison
with the binding energy of these nuclei shows that these values are
lower than the corresponding binding energies BA
by a factor of about 10, at least.
Thus, even when the thermal equilibrium is maintained, significant
synthesis of nuclei can occur only at T
 0.3 MeV and not
at higher temperatures.
If such is the case, then we would expect significant production
(XA
0.3 MeV and not
at higher temperatures.
If such is the case, then we would expect significant production
(XA 1) of nuclear species-A at temperatures T
1) of nuclear species-A at temperatures T
 TA. It turns out, however, that
the rate of nuclear reactions is not high enough to maintain
thermal equilibrium between various species. We have to determine the
temperatures up to which thermal equilibrium can be maintained and redo the
calculations to find non-equilibrium mass fractions.
The general procedure for studying non equilibrium abundances in an
expanding universe is based on rate equations. Since we will
require this formalism again in
Section 2.3 (for the study of recombination), we will
develop it in a somewhat general context.
TA. It turns out, however, that
the rate of nuclear reactions is not high enough to maintain
thermal equilibrium between various species. We have to determine the
temperatures up to which thermal equilibrium can be maintained and redo the
calculations to find non-equilibrium mass fractions.
The general procedure for studying non equilibrium abundances in an
expanding universe is based on rate equations. Since we will
require this formalism again in
Section 2.3 (for the study of recombination), we will
develop it in a somewhat general context.
Consider a reaction in which two particles 1 and 2 interact to form two
other particles 3 and 4. For example, n +
 e
e
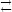 p+e constitutes one
such reaction which converts neutrons into protons in the forward direction
and protons into neutrons in the reverse direction; another example we
will come
across in the next section is p+e
p+e constitutes one
such reaction which converts neutrons into protons in the forward direction
and protons into neutrons in the reverse direction; another example we
will come
across in the next section is p+e
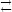 H +
H +
 where the
forward reaction describes recombination of electron and proton forming
a neutral hydrogen atom (with the emission of a photon), while the
reverse reaction is the photoionisation of a hydrogen atom. In general,
we are interested in how the number density n1 of
particle species 1, say, changes due to a reaction of the form 1 +
2
where the
forward reaction describes recombination of electron and proton forming
a neutral hydrogen atom (with the emission of a photon), while the
reverse reaction is the photoionisation of a hydrogen atom. In general,
we are interested in how the number density n1 of
particle species 1, say, changes due to a reaction of the form 1 +
2 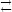 3 + 4.
3 + 4.
We first note that even if there is no reaction, the number density will
change as n1
 a-3
due to the expansion of the universe; so what we are really after
is the change in n1 a3. Further, the
forward reaction will be proportional to
the product of the number densities n1
n2 while the reverse reaction will be proportional
to n3 n4. Hence we can write an
equation for the rate of change of particle species
n1 as
a-3
due to the expansion of the universe; so what we are really after
is the change in n1 a3. Further, the
forward reaction will be proportional to
the product of the number densities n1
n2 while the reverse reaction will be proportional
to n3 n4. Hence we can write an
equation for the rate of change of particle species
n1 as
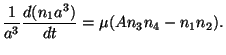 |
(22) |
The left hand side is the relevant rate of change over and above that
due to the expansion of the universe; on the right hand side, the two
proportionality constants have been written as
µ and (Aµ), both of which, of course,
will be functions of time.
(The quantity µ has the dimensions of
cm3s-1, so that nµ has the
dimensions of s-1; usually µ

 v where
v where
 is the cross-section
for the relevant process and v is
the relative velocity.) The left hand side has to vanish
when the system is in thermal equilibrium with ni =
nieq, where
the superscript `eq' denotes the equilibrium densities for the different
species labeled by i=1 - 4. This condition allows us to rewrite
A as A = n1eq
n2eq / (n3eq
n4eq). Hence the rate equation becomes
is the cross-section
for the relevant process and v is
the relative velocity.) The left hand side has to vanish
when the system is in thermal equilibrium with ni =
nieq, where
the superscript `eq' denotes the equilibrium densities for the different
species labeled by i=1 - 4. This condition allows us to rewrite
A as A = n1eq
n2eq / (n3eq
n4eq). Hence the rate equation becomes
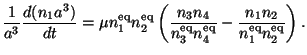 |
(23) |
In the left hand side, one can write (d / dt) = H a (d / da) which shows that the relevant time scale governing the process is H-1. Clearly, when H / nµ >> 1 the right hand side becomes ineffective because of the (µ / H) factor and the number of particles of species 1 does not change. We see that when the expansion rate of the universe is large compared to the reaction rate, the given reaction is ineffective in changing the number of particles. This certainly does not mean that the reactions have reached thermal equilibrium and ni = nieq; in fact, it means exactly the opposite: The reactions are not fast enough to drive the number densities towards equilibrium densities and the number densities "freeze out" at non equilibrium values. Of course, the right hand side will also vanish when ni = nieq which is the other extreme limit of thermal equilibrium.
Having taken care of the general formalism, let us now
apply it to the process of nucleosynthesis
which requires protons and neutrons combining together to form bound
nuclei of heavier
elements like deuterium, helium etc.. The abundance of these elements
are going to be determined by the relative abundance of neutrons and protons
in the universe. Therefore, we need to first worry about the maintenance
of thermal equilibrium between protons and the neutrons in the early
universe. As long as the inter-conversion between n and p
through the weak interaction processes
( + n
+ n
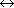 p+e),
(
p+e),
( + n
+ n
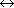 p +
p +
 ) and the `decay'
(n
) and the `decay'
(n 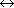 p + e +
p + e +  ),
is rapid (compared to the
expansion rate of the universe), thermal equilibrium will be
maintained. Then the equilibrium (n / p) ratio will be
),
is rapid (compared to the
expansion rate of the universe), thermal equilibrium will be
maintained. Then the equilibrium (n / p) ratio will be
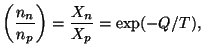 |
(24) |
where Q = mn - mp = 1.293
MeV. At high (T >> Q) temperatures, there will be equal
number of neutrons and protons but as the temperature drops below about
1.3 MeV, the neutron fraction will start dropping exponentially provided
thermal equilibrium is still maintained. To check whether thermal
equilibrium is indeed maintained, we need to compare the expansion rate
with the reaction rate. The expansion rate is given by H =
(8 G
G
 / 3)1/2
where
/ 3)1/2
where  =
(
=
( 2 / 30) g
T4 with g
2 / 30) g
T4 with g
 10.75 representing
the effective relativistic degrees of freedom present at these temperatures.
At T = Q, this gives H
10.75 representing
the effective relativistic degrees of freedom present at these temperatures.
At T = Q, this gives H
 1.1
s-1. The reaction rate needs to be computed from weak
interaction theory. The neutron to proton conversion rate, for example,
is well approximated by
1.1
s-1. The reaction rate needs to be computed from weak
interaction theory. The neutron to proton conversion rate, for example,
is well approximated by
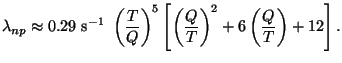 |
(25) |
At T=Q, this gives

 5 s-1,
slightly more rapid than the expansion rate. But as T drops below
Q, this decreases rapidly
and the reaction ceases to be fast enough to maintain thermal equilibrium.
Hence we need to work out the neutron abundance by using
Eq.(23).
5 s-1,
slightly more rapid than the expansion rate. But as T drops below
Q, this decreases rapidly
and the reaction ceases to be fast enough to maintain thermal equilibrium.
Hence we need to work out the neutron abundance by using
Eq.(23).
Using n1 = nn, n3 = np and n2, n4 = nl where the subscript l stands for the leptons, Eq.(23) becomes
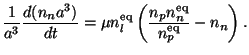 |
(26) |
We now use Eq.(24), write (nleqµ)
=  np which is
the rate for neutron to proton conversion and introduce the fractional
abundance Xn = nn /
(nn + np).
Simple manipulation then leads to the equation
np which is
the rate for neutron to proton conversion and introduce the fractional
abundance Xn = nn /
(nn + np).
Simple manipulation then leads to the equation
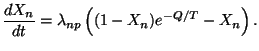 |
(27) |
Converting from the variable t to the variable s = (Q / T) and using (d / dt) = - HT(d / dT), the equations we need to solve reduce to
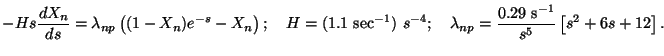 |
(28) |
It is now straightforward to integrate these equations numerically and determine how the neutron abundance changes with time. The neutron fraction fall out of equilibrium when temperatures drop below 1 MeV and it freezes to about 0.15 at temperatures below 0.5 MeV.
As the temperature decreases further, the neutron decay with a half
life of  n
n
 886.7 sec (which is
not included in the above analysis) becomes important and starts
depleting the neutron number density. The only way neutrons can survive
is through the synthesis of light elements.
As the temperature falls further to T = THe
886.7 sec (which is
not included in the above analysis) becomes important and starts
depleting the neutron number density. The only way neutrons can survive
is through the synthesis of light elements.
As the temperature falls further to T = THe
 0.28 MeV,
significant amount of He could have been produced if the nuclear
reaction rates were high enough. The possible reactions which produces
4He are [D(D,n)
3He(D,p)
4He, D(D,p)
3H(D,n)
4He, D(D,
0.28 MeV,
significant amount of He could have been produced if the nuclear
reaction rates were high enough. The possible reactions which produces
4He are [D(D,n)
3He(D,p)
4He, D(D,p)
3H(D,n)
4He, D(D,
 )
4He].
These are all based on D, 3He and
3H and do not occur rapidly enough
because the mass fraction of D, 3He and
3H are still quite
small [10-12, 10-19 and 5× 10-19
respectively]
at T
)
4He].
These are all based on D, 3He and
3H and do not occur rapidly enough
because the mass fraction of D, 3He and
3H are still quite
small [10-12, 10-19 and 5× 10-19
respectively]
at T  0.3 MeV.
The reactions n + p
0.3 MeV.
The reactions n + p
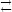 d+
d+ will lead to an equilibrium abundance ratio of deuterium given by
will lead to an equilibrium abundance ratio of deuterium given by
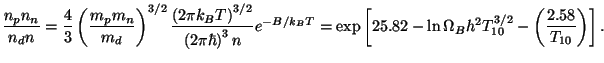 |
(29) |
The equilibrium deuterium abundance passes through unity
(for  B
h2 = 0.02) at the temperature of about 0.07 MeV
which is when the nucleosynthesis can really begin.
B
h2 = 0.02) at the temperature of about 0.07 MeV
which is when the nucleosynthesis can really begin.
So we need to determine the neutron fraction at T = 0.07 MeV
given that it was about 0.15 at 0.5 MeV. During this epoch, the
time-temperature relationship is given by t = 130 sec (T /
0.1 MeV)-2. The neutron decay factor is
exp(-t/ n)
n)
 0.74 for T = 0.07 MeV. This decreases the neutron fraction to 0.15
× 0.74 = 0.11 at the time of nucleosynthesis.
When the temperature becomes T
0.74 for T = 0.07 MeV. This decreases the neutron fraction to 0.15
× 0.74 = 0.11 at the time of nucleosynthesis.
When the temperature becomes T
 0.07 MeV, the
abundance of D and
3H builds up and these elements further react to form
4He. A
good fraction of D and 3H is converted to
4He (See
Fig. 1 which shows the growth of deuterium
and its subsequent fall when helium is built up). The resultant abundance
of 4He can be easily calculated by assuming that
almost all neutrons
end up in 4He. Since each 4He
nucleus has two neutrons, (nn/2) helium nuclei
can be formed (per unit volume) if the number density of neutrons is
nn.
Thus the mass fraction of 4He will be
0.07 MeV, the
abundance of D and
3H builds up and these elements further react to form
4He. A
good fraction of D and 3H is converted to
4He (See
Fig. 1 which shows the growth of deuterium
and its subsequent fall when helium is built up). The resultant abundance
of 4He can be easily calculated by assuming that
almost all neutrons
end up in 4He. Since each 4He
nucleus has two neutrons, (nn/2) helium nuclei
can be formed (per unit volume) if the number density of neutrons is
nn.
Thus the mass fraction of 4He will be
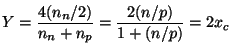 |
(30) |
where xc = n / (n + p) is the
neutron abundance at the time of production of deuterium. For
 B
h2 = 0.02, xc
B
h2 = 0.02, xc
 0.11 giving Y
0.11 giving Y
 0.22. Increasing
baryon density to
0.22. Increasing
baryon density to
 B
h2 = 1 will make Y
B
h2 = 1 will make Y
 0.25.
An accurate fitting formula for the dependence of helium abundance on
various parameters is given by
0.25.
An accurate fitting formula for the dependence of helium abundance on
various parameters is given by
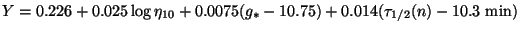 |
(31) |
where
 10
measures the baryon-photon ratio today via Eq.(19)
and g* is the effective number of
relativistic degrees of freedom contributing to the energy density and
10
measures the baryon-photon ratio today via Eq.(19)
and g* is the effective number of
relativistic degrees of freedom contributing to the energy density and
 1/2 (n) is
the neutron half life. The results (of a more exact treatment) are shown
in Fig. 1.
1/2 (n) is
the neutron half life. The results (of a more exact treatment) are shown
in Fig. 1.
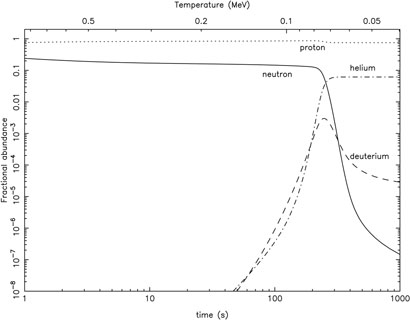 |
Figure 1. The evolution of mass fraction of different species during nucleosynthesis |
As the reactions converting D and 3H to
4He proceed, the number
density of D and 3H is depleted and the
reaction rates - which are proportional to

 XA(
XA( n
n )
<
)
< v> -
become small. These reactions soon freeze-out leaving a
residual fraction of D and 3H (a fraction of
about 10-5 to 10-4). Since
v> -
become small. These reactions soon freeze-out leaving a
residual fraction of D and 3H (a fraction of
about 10-5 to 10-4). Since


 it is clear
that the fraction of
(D, 3H) left unreacted will decrease with
it is clear
that the fraction of
(D, 3H) left unreacted will decrease with
 . In contrast, the
4He synthesis - which is not limited by any reaction
rate - is fairly independent of
. In contrast, the
4He synthesis - which is not limited by any reaction
rate - is fairly independent of
 and depends
only on the (n / p) ratio at
T
and depends
only on the (n / p) ratio at
T  0.1 MeV.
The best fits, with typical errors, to deuterium abundance
calculated from the theory, for the range
0.1 MeV.
The best fits, with typical errors, to deuterium abundance
calculated from the theory, for the range
 =
(10-10 - 10-9) is given by
=
(10-10 - 10-9) is given by
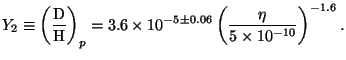 |
(32) |
The production of still heavier elements - even those like 16C, 16O which have higher binding energies than 4He - is suppressed in the early universe. Two factors are responsible for this suppression: (1) For nuclear reactions to proceed, the participating nuclei must overcome their Coulomb repulsion. The probability to tunnel through the Coulomb barrier is governed by the factor F = exp[-2 A1/3 (Z1 Z2)2/3(T / 1 MeV)-1/3] where A-1 = A1-1 + A2-1. For heavier nuclei (with larger Z), this factor suppresses the reaction rate. (2) Reaction between helium and proton would have led to an element with atomic mass 5 while the reaction of two helium nuclei would have led to an element with atomic mass 8. However, there are no stable elements in the periodic table with the atomic mass of 5 or 8! The 8Be, for example, has a half life of only 10-16 seconds. One can combine 4He with 8Be to produce 12C but this can occur at significant rate only if it is a resonance reaction. That is, there should exist an excited state 12C nuclei which has an energy close to the interaction energy of 4He + 8Be. Stars, incidentally, use this route to synthesize heavier elements. It is this triple-alpha reaction which allows the synthesis of heavier elements in stars but it is not fast enough in the early universe. (You must thank your stars that there is no such resonance in 16O or in 20Ne - which is equally important for the survival of carbon and oxygen.)
The current observations indicate, with reasonable certainty
that: (i) (D / H)  1 × 10-5. (ii) [(D +
3He) / H]
1 × 10-5. (ii) [(D +
3He) / H]
 (1-8)×
10-5 and (iii) 0.236 < (4He / H)
<0.254. These observations are consistent with the predictions if
10.3 min
(1-8)×
10-5 and (iii) 0.236 < (4He / H)
<0.254. These observations are consistent with the predictions if
10.3 min

 10.7 min, and
10.7 min, and
 = (3 - 10)
× 10-10.
Using
= (3 - 10)
× 10-10.
Using  = 2.68
× 10-8
= 2.68
× 10-8
 B
h2, this leads to the important conclusion:
0.011
B
h2, this leads to the important conclusion:
0.011 
 B
h2
B
h2  0.037.
When combined with the broad bounds on h, 0.6
0.037.
When combined with the broad bounds on h, 0.6
 h
h
 0.8,
say, we can constrain the baryonic density of the universe to be:
0.01
0.8,
say, we can constrain the baryonic density of the universe to be:
0.01 
 B
B
 0.06.
These are the typical bounds on
0.06.
These are the typical bounds on
 B
available today. It shows that, if
B
available today. It shows that, if
 total
total
 1 then most of the
matter in the universe must be non baryonic.
1 then most of the
matter in the universe must be non baryonic.
Since the 4He production depends on g, the
observed value of 4He restricts
the total energy density present at the time of nucleosynthesis. In
particular, it constrains the number
(N ) of light neutrinos (that is, neutrinos with
m
) of light neutrinos (that is, neutrinos with
m
 1 MeV which would
have been relativistic at
T
1 MeV which would
have been relativistic at
T  1 MeV). The
observed abundance is best explained by
N
1 MeV). The
observed abundance is best explained by
N = 3, is barely consistent with
N
= 3, is barely consistent with
N = 4 and rules out
N
= 4 and rules out
N > 4. The laboratory bound on the total number of particles including
neutrinos, which couples to
the Z0 boson is determined by measuring the decay
width of the particle Z0; each particle with mass less
than (mz / 2)
> 4. The laboratory bound on the total number of particles including
neutrinos, which couples to
the Z0 boson is determined by measuring the decay
width of the particle Z0; each particle with mass less
than (mz / 2)
 46 GeV contributes
about 180 MeV to this decay width. This bound is
N
46 GeV contributes
about 180 MeV to this decay width. This bound is
N = 2.79 ± 0.63 which is consistent with the cosmological observations.
= 2.79 ± 0.63 which is consistent with the cosmological observations.
2.3. Decoupling of matter and radiation
In the early hot phase, the radiation will be in thermal equilibrium with
matter; as the universe cools below kB T
 (
( a / 10)
where
a / 10)
where  a
is the binding energy of atoms, the electrons and ions will combine
to form neutral atoms and radiation will decouple from matter. This occurs
at Tdec
a
is the binding energy of atoms, the electrons and ions will combine
to form neutral atoms and radiation will decouple from matter. This occurs
at Tdec
 3 × 103 K.
As the universe expands further, these photons will continue to exist
without any further interaction. It will retain thermal
spectrum since the redshift of the frequency
3 × 103 K.
As the universe expands further, these photons will continue to exist
without any further interaction. It will retain thermal
spectrum since the redshift of the frequency

 a-1 is
equivalent to changing the temperature in the spectrum by the scaling
T
a-1 is
equivalent to changing the temperature in the spectrum by the scaling
T (1 / a).
It turns out that the major component of the extra-galactic
background light (EBL) which exists today is in the microwave band and
can be fitted very accurately by
a thermal spectrum at a temperature of about 2.73 K.
It seems reasonable to interpret this radiation as a relic arising
from the early, hot, phase of the evolving universe.
This relic radiation, called cosmic microwave background
radiation, turns out to be a gold mine of cosmological information and
is extensively investigated in recent times. We shall now discuss some
details related to the formation of neutral atoms and the decoupling of
photons. Cosmic Microwave Background Radiation
(1 / a).
It turns out that the major component of the extra-galactic
background light (EBL) which exists today is in the microwave band and
can be fitted very accurately by
a thermal spectrum at a temperature of about 2.73 K.
It seems reasonable to interpret this radiation as a relic arising
from the early, hot, phase of the evolving universe.
This relic radiation, called cosmic microwave background
radiation, turns out to be a gold mine of cosmological information and
is extensively investigated in recent times. We shall now discuss some
details related to the formation of neutral atoms and the decoupling of
photons. Cosmic Microwave Background Radiation
The relevant reaction is, of course, e + p
 H
+
H
+ and if
the rate of this reaction is faster than the expansion
rate, then one can calculate the neutral fraction using Saha's equation.
Introducing the fractional ionisation,
Xi, for each of the particle species
and using the facts np = ne and
np + nH = nB, it
follows that
Xp = Xe and XH =
(nH / nB) = 1 -
Xe. Saha's equation now gives
and if
the rate of this reaction is faster than the expansion
rate, then one can calculate the neutral fraction using Saha's equation.
Introducing the fractional ionisation,
Xi, for each of the particle species
and using the facts np = ne and
np + nH = nB, it
follows that
Xp = Xe and XH =
(nH / nB) = 1 -
Xe. Saha's equation now gives
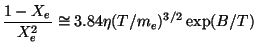 |
(33) |
where  = 2.68
× 10-8(
= 2.68
× 10-8( B h2) is the baryon-to-photon
ratio. We may define Tatom as the temperature at which
90 percent of the electrons, say, have combined with protons: i.e. when
Xe = 0.1. This leads to the condition:
B h2) is the baryon-to-photon
ratio. We may define Tatom as the temperature at which
90 percent of the electrons, say, have combined with protons: i.e. when
Xe = 0.1. This leads to the condition:
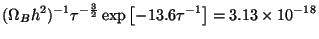 |
(34) |
where  = (T / 1
eV). For a given value of
(
= (T / 1
eV). For a given value of
( B
h2), this equation can be easily solved by iteration.
Taking logarithms and iterating once we find
B
h2), this equation can be easily solved by iteration.
Taking logarithms and iterating once we find
 -1
-1
 3.084 -
0.0735ln(
3.084 -
0.0735ln( B
h2) with the corresponding redshift (1 + z) =
(T / T0) given by
B
h2) with the corresponding redshift (1 + z) =
(T / T0) given by
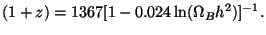 |
(35) |
For  B
h2 = 1, 0.1,0.01 we get Tatom
B
h2 = 1, 0.1,0.01 we get Tatom
 0.324 eV, 0.307 eV,
0.292 eV respectively. These values correspond to the redshifts of
1367, 1296 and 1232.
0.324 eV, 0.307 eV,
0.292 eV respectively. These values correspond to the redshifts of
1367, 1296 and 1232.
Because the preceding analysis was based on equilibrium densities, it is
important to check that the rate of the reactions p + e
 H +
H +
 is fast enough to maintain equilibrium.
For
is fast enough to maintain equilibrium.
For  B
h2
B
h2  0.02, the equilibrium condition is only marginally
satisfied, making this analysis suspect. More importantly, the direct
recombination to the ground state of the hydrogen atom - which was used in
deriving the Saha's equation - is not very effective in producing neutral
hydrogen in the early universe. The problem is that each such recombination
releases a photon of energy 13.6 eV which will end up ionizing another
neutral hydrogen atom which has been formed earlier. As a result, the
direct recombination to the ground state does not change the neutral
hydrogen fraction at the lowest order. Recombination through the
excited states of hydrogen is more effective since such a recombination
ends up emitting more than one photon each of which has an energy less
than 13.6 eV. Given these facts, it is necessary to once again use the
rate equation developed in the previous section to track the evolution
of ionisation fraction.
0.02, the equilibrium condition is only marginally
satisfied, making this analysis suspect. More importantly, the direct
recombination to the ground state of the hydrogen atom - which was used in
deriving the Saha's equation - is not very effective in producing neutral
hydrogen in the early universe. The problem is that each such recombination
releases a photon of energy 13.6 eV which will end up ionizing another
neutral hydrogen atom which has been formed earlier. As a result, the
direct recombination to the ground state does not change the neutral
hydrogen fraction at the lowest order. Recombination through the
excited states of hydrogen is more effective since such a recombination
ends up emitting more than one photon each of which has an energy less
than 13.6 eV. Given these facts, it is necessary to once again use the
rate equation developed in the previous section to track the evolution
of ionisation fraction.
A simple procedure for doing this, which captures the
essential physics, is as follows: We again begin with Eq. (23) and
repeating the analysis done in the last section, now with
n1 = ne, n2 =
np, n3 = nH and
n4 =
n ,
and defining Xe = ne /
(ne + nH) = np/
nH one can easily derive the rate equation for this case:
,
and defining Xe = ne /
(ne + nH) = np/
nH one can easily derive the rate equation for this case:
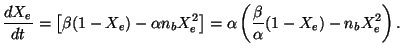 |
(36) |
This equation is analogous to Eq. (27); the first term gives the
photoionisation rate which produces the free electrons and the second
term is the recombination
rate which converts free electrons into hydrogen atom and we have used the
fact ne = nb Xe
etc.. Since we know that direct recombination to the ground
state is not effective, the recombination rate
 is the rate for
capture of electron by a proton forming an excited state of hydrogen.
To a good approximation, this rate is given by
is the rate for
capture of electron by a proton forming an excited state of hydrogen.
To a good approximation, this rate is given by
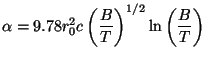 |
(37) |
where r0 = e2 / me
c2 is the classical electron radius. To integrate
Eq. (36) we also need to know
 /
/
 . This is easy because
in thermal equilibrium the right hand side of Eq. (36) should vanish
and Saha's equation tells us the value of Xe in
thermal equilibrium. On using Eq. (33), this gives
. This is easy because
in thermal equilibrium the right hand side of Eq. (36) should vanish
and Saha's equation tells us the value of Xe in
thermal equilibrium. On using Eq. (33), this gives
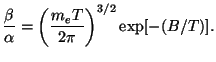 |
(38) |
We can now integrate Eq. (36) using the variable B / T
just as we used the variable Q / T in solving
Eq. (27). The result shows that the actual recombination proceeds more
slowly compared to that predicted by the Saha's equation.
The actual fractional ionisation is higher
than the value predicted by Saha's equation at temperatures below about
1300. For example, at z = 1300, these values differ by a factor 3;
at z  900, they
differ by a factor of 200. The value of
Tatom, however, does not change significantly.
A more rigorous analysis shows that, in the redshift range
of 800 < z < 1200, the fractional ionisation varies rapidly
and is given (approximately) by the formula,
900, they
differ by a factor of 200. The value of
Tatom, however, does not change significantly.
A more rigorous analysis shows that, in the redshift range
of 800 < z < 1200, the fractional ionisation varies rapidly
and is given (approximately) by the formula,
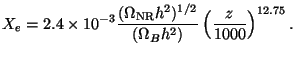 |
(39) |
This is obtained by fitting a curve to the numerical solution.
The formation of neutral atoms makes the photons decouple from the matter. The redshift for decoupling can be determined as the epoch at which the optical depth for photons is unity. Using Eq. (39), we can compute the optical depth for photons to be
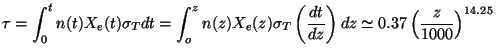 |
(40) |
where we have used the relation H0 dt
 -
- NR-1/2 z-5/2
dz which is valid for z >> 1.
This optical depth is unity at zdec=1072.
From the optical depth, we can also compute the probability that the
photon was last scattered in the interval (z, z +
dz). This is given by
(exp -
NR-1/2 z-5/2
dz which is valid for z >> 1.
This optical depth is unity at zdec=1072.
From the optical depth, we can also compute the probability that the
photon was last scattered in the interval (z, z +
dz). This is given by
(exp - )
(d
)
(d / dz) which
can be expressed as
/ dz) which
can be expressed as
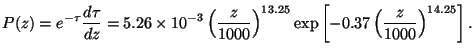 |
(41) |
This P(z) has a sharp maximum at z
 1067 and a width of about
1067 and a width of about
 z
z
 80. It is therefore
reasonable to assume that decoupling occurred at z
80. It is therefore
reasonable to assume that decoupling occurred at z
 1070 in an interval of
about
1070 in an interval of
about  z
z
 80.
We shall see later that the finite thickness of the
surface of last scattering has important observational consequences.
80.
We shall see later that the finite thickness of the
surface of last scattering has important observational consequences.