3. STRUCTURE FORMATION AND LINEAR PERTURBATION THEORY

Having discussed the evolution of the background universe, we now turn to the study of structure formation. Before discussing the details, let us briefly summarise the broad picture and give references to some of the topics that we will not discuss. The key idea is that if there existed small fluctuations in the energy density in the early universe, then gravitational instability can amplify them in a well-understood manner leading to structures like galaxies etc. today. The most popular model for generating these fluctuations is based on the idea that if the very early universe went through an inflationary phase [9], then the quantum fluctuations of the field driving the inflation can lead to energy density fluctuations [10 , 11]. It is possible to construct models of inflation such that these fluctuations are described by a Gaussian random field and are characterized by a power spectrum of the form P(k) = A kⁿ with n 1 (see Sec. 7). The models cannot predict the value of the amplitude A in an unambiguous manner but it can be determined from CMBR observations. The CMBR observations are consistent with the inflationary model for the generation of perturbations and gives A (28.3 h^-1 Mpc)⁴ and n = 0.97 ± 0.023 (The first results were from COBE [12] and WMAP has reconfirmed them with far greater accuracy). When the perturbation is small, one can use well defined linear perturbation theory to study its growth. But when ( / ) is comparable to unity the perturbation theory breaks down. Since there is more power at small scales, smaller scales go non-linear first and structure forms hierarchically. The non linear evolution of the dark matter halos (which is an example of statistical mechanics of self gravitating systems; see e.g. [13]) can be understood by simulations as well as theoretical models based on approximate ansatz [14] and nonlinear scaling relations [15]. The baryons in the halo will cool and undergo collapse in a fairly complex manner because of gas dynamical processes. It seems unlikely that the baryonic collapse and galaxy formation can be understood by analytic approximations; one needs to do high resolution computer simulations to make any progress [16]. All these results are broadly consistent with observations.

As long as these fluctuations are small, one can study their evolution by linear perturbation theory, which is what we will start with [17]. The basic idea of linear perturbation theory is well defined and simple. We perturb the background FRW metric by g_ik^FRW g_ik^FRW + h_ik and also perturb the source energy momentum tensor by T_ik^FRW T_ik^FRW + T_ik. Linearising the Einstein's equations, one can relate the perturbed quantities by a relation of the form (g_ik^FRW) h_ik = T_ik where is second order linear differential operator depending on the back ground metric g_ik^FRW . Since the background is maximally symmetric, one can separate out time and space; for e.g, if k = 0, simple Fourier modes can be used for this purpose and we can write down the equation for any given mode, labelled by a wave vector k as:

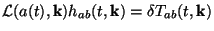(42)

To every mode we can associate a wavelength normalized to today's value: (t) = (2 / k)(1 + z)^-1 and a corresponding mass scale which is invariant under expansion:

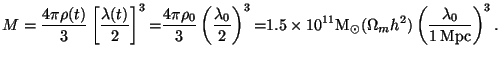(43)

The behaviour of the mode depends on the relative value of (t) as compared to the Hubble radius d_H(t) ( / a)^-1. Since the Hubble radius: d_H(t) t while the wavelength of the mode: (t) a(t) (t^1/2, t^2/3) in the radiation dominated and matter dominated phases it follows that (t) > d_H(t) at sufficiently early times. When (t) = d_H(t), we say that the mode is entering the Hubble radius. Since the Hubble radius at z = z_eq is

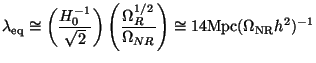(44)

it follows that modes with ₀ > _eq enter Hubble radius in MD phase while the more relevant modes with < _eq enter in the RD phase. Thus, for a given mode we can identify three distinct phases: First, very early on, when > d_H, z > z_eq the dynamics is described by general relativity. In this stage, the universe is radiation dominated, gravity is the only relevant force and the perturbations are linear. Next, when < d_H and z > z_eq one can describe the dynamics by Newtonian considerations. The perturbations are still linear and the universe is radiation dominated. Finally, when < d_H, z < z_eq we have a matter dominated universe in which we can use the Newtonian formalism; but at this stage - when most astrophysical structures form - we need to grapple with nonlinear astrophysical processes.

Let us now consider the metric perturbation in greater detail. When the metric is perturbed to the form: g_ab g_ab + h_ab the perturbation can be split as h_ab = (h₀₀, h₀ w, h). We also know that any 3-vector w(x) can be split as w = w + w^|| in which w^|| = ^|| is curl-free (and carries one degree of freedom) while w is divergence-free (and has 2 degrees of freedom). This result is obvious in k-space since we can write any vector w(k) as a sum of two terms, one along k and one transverse to k:

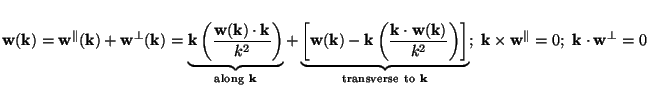(45)

Fourier transforming back, we can split w into a curl-free and divergence-free parts. Similar decomposition works for h by essentially repeating the above analysis on each index. We can write:

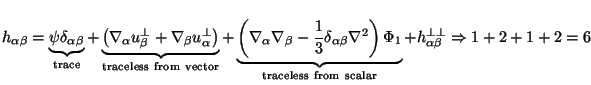(46)

The u is divergence free and h is traceless and divergence free. Thus the most general perturbation h_ab (ten degrees of freedom) can be built out of

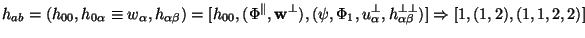(47)

We now use the freedom available in the choice of four coordinate transformations to set four conditions: ^|| = ₁ = 0 and u = 0 thereby leaving six degrees of freedom in (h₀₀ 2, , w, h ) as nonzero. Then the perturbed line element takes the form:

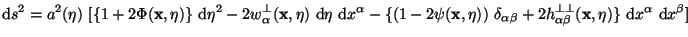(48)

To make further simplification we need to use two facts from Einstein's equations. It turns out that the Einstein's equations for w and h decouple from those for (, ). Further, in the absence of anisotropic stress, one of the equations give = . If we use these two facts, we can simplify the structure of perturbed metric drastically. As far as the growth of matter perturbations are concerned, we can ignore w and h and work with a simple metric:

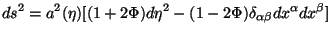(49)

with just one perturbed scalar degree of freedom in . This is what we will study.

Having decided on the gauge, let us consider the evolution equations for the perturbations. While one can directly work with the Einstein's equations, it turns out to be convenient to use the equations of motion for matter variables, since we are eventually interested in the matter perturbations. In what follows, we will use the over-dot to denote (d / d) so that the standard Hubble parameter is H = (1 / a)(da / dt) = / a². With this notation, the continuity equation becomes:

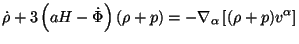(50)

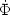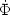Since the momentum flux in the relativistic case is ( + p) v, all the terms in the above equation are intuitively obvious, except probably the term. To see the physical origin of this term, note that the perturbation in Eq. (49) changes the factor in front of the spatial metric from a² to a²(1 - 2) so that lna lna - ; hence the effective Hubble parameter from ( / a) to ( / a) - which explains the extra 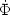term. This is, of course, the exact equation for matter variables in the perturbed metric given by Eq. (49); but we only need terms which are of linear order. Writing the curl-free velocity part as v = v, the linearised equations, for dark matter (with p=0) and radiation (with p = (1/3) ) perturbations are given by:

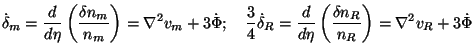(51)

where n_m and n_R are the number densities of dark matter particles and radiation. The same equations in Fourier space [using the same symbols for, say, (t,x) or (t,k)] are simpler to handle:

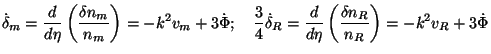(52)

Note that these equations imply

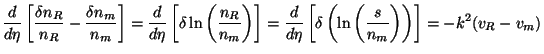(53)

For long wavelength perturbations (in the limit of k 0), this will lead to the conservation of perturbation (s / n_m) in the entropy per particle.

Let us next consider the Euler equation which has the general form:

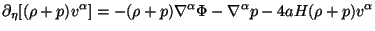(54)

Once again each of the terms is simple to interpret. The ( + p) arises because the pressure also contributes to inertia in a relativistic theory and the factor 4 in the last term on the right hand side arises because the term v ( + p) on the left hand side needs to be compensated. Taking the linearised limit of this equation, for dark matter and radiation, we get:

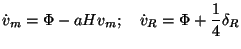(55)

Thus we now have four equations in Eqs. (52), (55) for the five variables (_m, _R, v_m, v_R, ). All we need to do is to pick one more from Einstein's equations to complete the set. The Einstein's equations for our perturbed metric are:

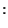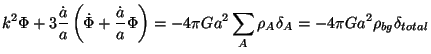			(56)
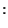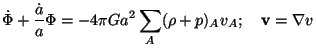			(57)
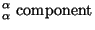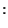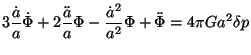			(58)

where A denotes different components like dark matter, radiation etc. Using Eq. (57) in Eq. (56) we can get a modified Poisson equation which is purely algebraic:

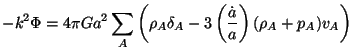(59)

which once again emphasizes the fact that in the relativistic theory, both pressure and density act as source of gravity.

To get a feel for the solutions let us consider a flat universe dominated by a single component of matter with the equation of state p = w . (A purely radiation dominated universe, for example, will have w = 1/3.) In this case the Friedmann background equation gives a^{-3 (1 + w)} and

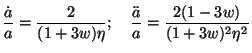(60)

The equation for the potential can be reduced to the form:

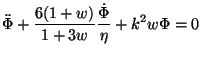(61)

The second term is the damping due to the expansion while last term is the pressure support that will lead to oscillations. Clearly, the factor k determines which of these two terms dominates. When the pressure term dominates (k >> 1), we expect oscillatory behaviour while when the background expansion dominates (k << 1), we expect the growth to be suppressed. This is precisely what happens. The exact solution is given in terms of the Bessel functions

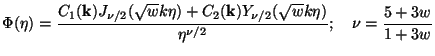(62)

From the theory of Bessel functions, we know that:

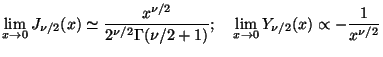(63)

This shows that if we want a finite value for as 0, we can set C₂ = 0. This gives the gravitational potential to be

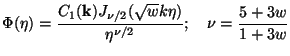(64)

The corresponding density perturbation will be:

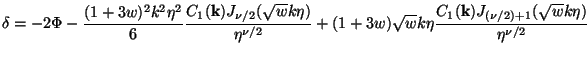(65)

To understand the nature of the solution, note that d_H = ( / a)^-1 and kd_H d_H / k. So the argument of the Bessel function is just the ratio (d_H / ). From the theory of Bessel functions, we know that for small values of the argument J(x) x is a power law while for large values of the argument it oscillates with a decaying amplitude:

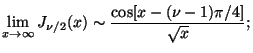(66)

Hence, for modes which are still outside the Hubble radius (k << ^-1), we have a constant amplitude for the potential and density contrast:

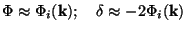(67)

That is, the perturbation is frozen (except for a decaying mode) at a constant value. On the other hand, for modes which are inside the Hubble radius (k >> ^-1), the perturbation is rapidly oscillatory (if w 0). That is the pressure is effective at small scales and leads to acoustic oscillations in the medium.

A special case of the above is the flat, matter-dominated universe with w=0. In this case, we need to take the w 0 limit and the general solution is indeed a constant = _i(k) (plus a decaying mode _decay ^-5 which diverges as 0). The corresponding density perturbations is:

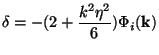(68)

which shows that density perturbation is "frozen" at large scales but grows at small scales:

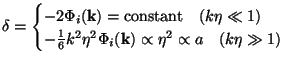(69)

We will use these results later on.