5. TRANSFER FUNCTION FOR MATTER PERTURBATIONS

We now have all the ingredients to evolve the matter perturbation from an initial value = _i at y = y_i << 1 to the current epoch y = y₀ = a_eq^-1 in the matter dominated phase at y >> 1. Initially, the wavelength of the perturbation will be bigger than the Hubble radius and the perturbation will essentially remain frozen. When it enters the Hubble radius in the radiation dominated phase, it begins to grow but only logarithmically (see section 4.2 ) until the universe becomes matter dominated. In the final matter dominated phase, the perturbation grows linearly with expansion factor. The relation between final and initial perturbation can be obtained by combining these results.

Usually, one is more interested in the power spectrum P_k(t) and the power per logarithmic band in k-space _k(t). These quantities are defined in terms of _k(t) through the equations:

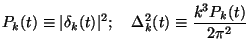(100)

It is therefore convenient to study the evolution of k^3/2 _k since its square will immediately give the power per logarithmic band _k² in k-space.

Let us first consider a mode which enters the Hubble radius in the radiation dominated phase at the epoch a_enter. From the scaling relation, a_ent / k t_ent a_ent² we find that y_ent = (k_eq / k). Hence

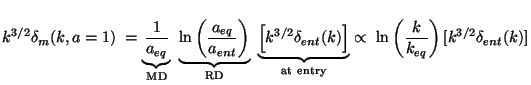(101)

where two factors - as indicated - gives the growth in radiation (RD) and matter dominated (MD) phases. Let us next consider the modes that enter in the matter dominated phase. In this case, a_ent / k t_ent a_ent^3/2 so that y_ent = (k_eq / k)². Hence

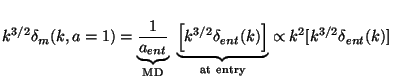(102)

To proceed further, we need to know the k-dependence of the perturbation when it enters the Hubble radius which, of course, is related to the mechanism that generates the initial power spectrum. The most natural choice will be that all the modes enter the Hubble radius with a constant amplitude at the time of entry. This would imply that the physical perturbations are scale invariant at the time of entering the Hubble radius, a possibility that was suggested by Zeldovich and Harrison [18] (years before inflation was invented!). We will see later that this is also true for perturbations generated by inflation and thus is a reasonable assumption at least in such models. Hence we shall assume

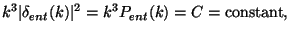(103)

Using this we find that the current value of perturbation is given by

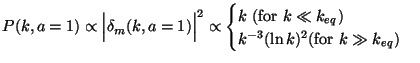(104)

The corresponding power per logarithmic band is

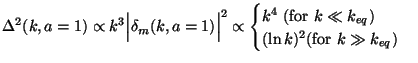(105)

The form for P(k) shows that the evolution imprints the scale k_eq on the power spectrum even though the initial power spectrum is scale invariant. For k < k_eq (for large spatial scales), the primordial form of the spectrum is preserved and the evolution only increases the amplitude preserving the shape. For k > k_eq (for small spatial scales), the shape is distorted and in general the power is suppressed in comparison with larger spatial scales. This arises because modes with small wavelengths enter the Hubble radius early on and have to wait till the universe becomes matter dominated in order to grow in amplitude. This is in contrast to modes with large wavelengths which continue to grow. It is this effect which suppresses the power at small wavelengths (for k > k_eq) relative to power at larger wavelengths.