6. TEMPERATURE ANISOTROPIES OF CMBR

We shall now apply the formalism we have developed to understand the temperature anisotropies in the cosmic microwave background radiation which is probably the most useful application of linear perturbation theory. We shall begin by developing the general formulation and the terminology which is used to describe the temperature anisotropies.

Towards every direction in the sky, n = (, ) we can define a fractional temperature fluctuation (n) (T / T) (, ). Expanding this quantity in spherical harmonics on the sky plane as well as in terms of the spatial Fourier modes, we get the two relations:

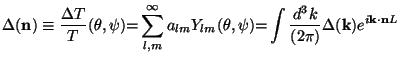(106)

where L = ₀ - _LSS is the distance to the last scattering surface (LSS) from which we are receiving the radiation. The last equality allows us to define the expansion coefficients a_lm in terms of the temperature fluctuation in the Fourier space (k) . Standard identities of mathematical physics now give

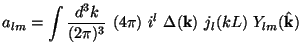(107)

Next, let us consider the angular correlation function of temperature anisotropy, which is given by:

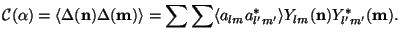(108)

where the wedges denote an ensemble average. For a Gaussian random field of fluctuations we can express the ensemble average as < a_lm a_l'm'^,tt>* > = C_{l ll' mm'}. Using Eq. (107), we get a relation between C_l and (k). Given (k), the C_l's are given by:

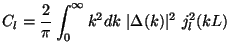(109)

Further, Eq. (108) now becomes:

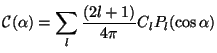(110)

Equation (110) shows that the mean-square value of temperature fluctuations and the quadrupole anisotropy corresponding to l = 2 are given by

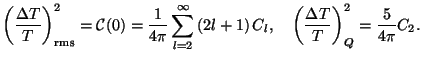(111)

These can be explicitly computed if we know (k) from the perturbation theory. (The motion of our local group through the CMBR leads to a large l = 1 dipole contribution in the temperature anisotropy. In the analysis of CMBR anisotropies, this is usually subtracted out. Hence the leading term is the quadrupole with l=2.)

It should be noted that, for a given l, the C_l is the average over all m = -l, ...-1, 0, 1, ... l. For a Gaussian random field, one can also compute the variance around this mean value. It can be shown that this variance in C_l is 2 C_l² / (2l + 1). In other words, there is an intrinsic root-mean-square fluctuation in the observed, mean value of C_l's which is of the order of C_l / C_l (2l + 1)^-1/2. It is not possible for any CMBR observations which measures the C_l's to reduce its uncertainty below this intrinsic variance - usually called the "cosmic variance". For large values of l, the cosmic variance is usually sub-dominant to other observational errors but for low l this is the dominant source of uncertainty in the measurement of C_l's. Current WMAP observations are indeed only limited by cosmic variance at low-l.

As an illustration of the formalism developed above, let us compute the C_l's for low l which will be contributed essentially by fluctuations at large spatial scales. Since these fluctuations will be dominated by gravitational effects, we can ignore the complications arising from baryonic physics and compute these using the formalism we have developed earlier.

We begin by noting that the redshift law of photons in the unperturbed Friedmann universe, ₀ = (a) / a, gets modified to the form ₀ = (a) / [a(1 + )] in a perturbed FRW universe. The argument of the Planck spectrum will thus scale as

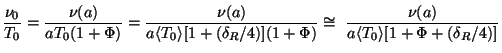(112)

This is equivalent to a temperature fluctuation of the amount

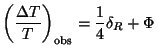(113)

at large scales. (Note that the observed T / T is not just (_R / 4) as one might have naively imagined.) To proceed further, we recall our large scale solution (see Eq. (78)) for the gravitational potential:

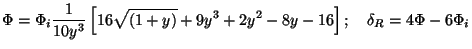(114)

At y=y_dec we can take the asymptotic solution _dec (9/10)_i. Hence we get

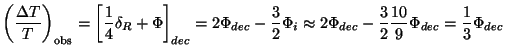(115)

We thus obtain the nice result that the observed temperature fluctuations at very large scales is simply related to the fluctuations of the gravitational potential at these scales. (For a discussion of the 1/3 factor, see [19]). Fourier transforming this result we get (k) = (1/3) (k, _LSS) where _LSS is the conformal time at the last scattering surface. (This contribution is called Sachs-Wolfe effect.) It follows from Eq. (109) that the contribution to C_l from the gravitational potential is

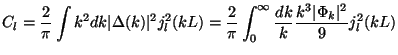(116)

with

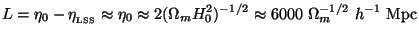(117)

For a scale invariant spectrum, k³ |_k|² is a constant independent of k. (Earlier on, in Eq. (103) we said that scale invariant spectrum has k³ |_k|² = constant. These statements are equivalent since -2 at the large scales because of Eq. (85) with the extra correction term in Eq. (85) being about 3× 10^-4 for k L^-1,y = y_dec.) As we shall see later, inflation generates such a perturbation. In this case, it is conventional to introduce a constant amplitude A and write:

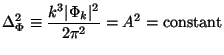(118)

Substituting this form into Eq. (116) and evaluating the integral, we find that

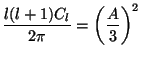(119)

As an application of this result, let us consider the observations of COBE which measured the temperature fluctuations for the first time in 1992. This satellite obtained the RMS fluctuations and the quadrupole after smoothing over an angular scale of about _c 10°. Hence the observed values are slightly different from those in Eq. (111). We have, instead,

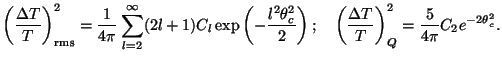(120)

Using Eqs. (118), (119) we find that

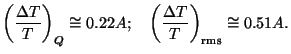(121)

Given these two measurements, one can verify that the fluctuations are consistent with the scale invariant spectrum by checking their ratio. Further, the numerical value of the observed (T / T) can be used to determine the amplitude A. One finds that A 3 × 10^-5 which sets the scale of fluctuations in the gravitational potential at the time when the perturbation enters the Hubble radius.

Incidentally, note that the solution _R = 4 - 6_i corresponds to _m = (3/4)_R = 3 - (9/2)_i. At y = y_dec, taking _dec = (9/10)_i, we get _m = 3_dec - (9/2)(10/9)_dec = -2_dec. Since (T / T)_obs = (1/3)_dec we get _m = -6(T / T)_obs. This shows that the amplitude of matter perturbations is a factor six larger that the amplitude of temperature anisotropy for our adiabatic initial conditions. In several other models, one gets _m = (1)(T / T)_obs. So, to reach a given level of nonlinearity in the matter distribution at later times, these models will require higher values of (T / T)_obs at decoupling. This is one reason for such models to be observationally ruled out.

There is another useful result which we can obtain from Eq. (109) along the same lines as we derived the Sachs-Wolfe effect. Whenever k³|(k)|² is a slowly varying function of k, we can pull out this factor out of the integral and evaluate the integral over j_l². This will give the result for any slowly varying k³ |(k)|²

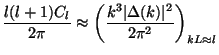(122)

This is applicable even when different processes contribute to temperature anisotropies as long as they add in quadrature. While far from accurate, it allows one to estimate the effects rapidly.

6.1. CMBR Temperature Anisotropy: More detailed theory

We shall now work out a more detailed theory of temperature anisotropies of CMBR so that one can understand the effects at small scales as well. A convenient starting point is the distribution function for photons with perturbed Planckian distribution, which we can write as:

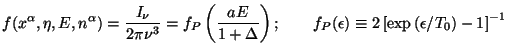(123)

The f_p() is the standard Planck spectrum for energy and we take = a E (1 + )^-1 to take care of the perturbations. In the absence of collisions, the distribution function is conserved along the trajectories of photons so that df / d = 0. So, in the presence of collisions, we can write the time evolution of the distribution function as

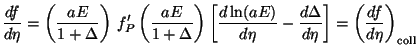(124)

where the right hand side gives the contribution due to collisional terms. Equivalently, in terms of , the same equation takes the form:

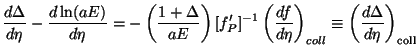(125)

To proceed further, we need the expressions for the two terms on the left hand side. First term, on using the standard expansion for total derivative, gives:

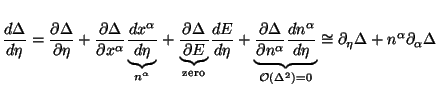(126)

(Note that we are assuming / E = 0 so that the perturbations do not depend on the frequency of the photon.) To determine the second term, we note that it vanishes in the unperturbed Friedmann universe and arises essentially due to the variation of . Both the intrinsic time variation of as well as its variation along the photon path will contribute, giving:

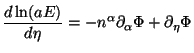(127)

(The minus sign arises from the fact that the we have (1 + 2) in g₀₀ but (1 - 2) in the spatial perturbations.) Putting all these together, we can bring the evolution equation Eq. (125) to the form:

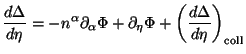(128)

Let us next consider the collision term, which can be expressed in the form:

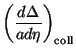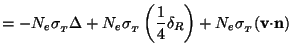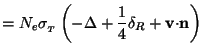		(129)

Each of the terms in the right hand side of the first line has a simple interpretation. The first term describes the removal of photons from the beam due to Thomson scattering with the electrons while the second term gives the scattering contribution into the beam. In a static universe, we expect these two terms to cancel if = (1/4)_R which fixes the relative coefficients of these two terms. The third term is a correction due to the fact that the electrons which are scattering the photons are not at rest relative to the cosmic frame. This leads to a Doppler shift which is accounted for by the third term. (We denote electron number density by N_e rather than n_e to avoid notational conflict with n.)

Formally, Eq. (128) is a first order linear differential equation for . To eliminate the -N_{e T} term which is linear in in the right hand side, we use the standard integrating factor exp(-) where

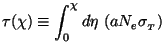(130)

We can then formally integrate Eq. (128) to get:

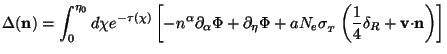(131)

We can write

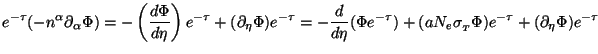(132)

On integration, the first term gives zero at the lower limit and an unimportant constant (which does not depend on n). Using the rest of the terms, we can write Eq. (131) in the form:

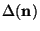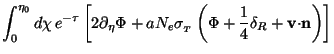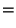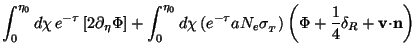			(133)

The first term gives the contribution due to the intrinsic time variation of the gravitational potential along the path of the photon and is called the integrated Sachs-Wolfe effect. In the second term one can make further simplifications. Note that e^- is essentially unity (optically thin) for z < z_rec and zero (optically thick) for z > z_rec; on the other hand, N_{e T} is zero for z < z_rec (all the free electrons have disappeared) and is large for z > z_rec. Hence the product (a N_e e^- ) is sharply peaked at = _rec (i.e. at z 10³ with z 80 ). Treating this sharply peaked quantity as essentially a Dirac delta function (usually called the instantaneous recombination approximation) we can approximate the second term in Eq. (133) as a contribution occurring just on the LSS:

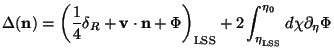(134)

In the second term we have put = for < _LSS and = 0 for > _LSS.

Once we know _R, and v on the LSS from perturbation theory, we can take a Fourier transform of this result to obtain (k) and use Eq. (109) to compute C_l. At very large scales the velocity term is sub-dominant and we get back the Sachs-Wolfe effect derived earlier in Eq. (118). For understanding the small scale effects, we need to introduce baryons into the picture which is our next task.

6.2. Description of photon-baryon fluid

To study the interaction of photons and baryons in the fluid limit, we need to again start from the continuity equation and Euler equation. In Fourier space, the continuity equation is same as the one we had before (see Eq. (52)):

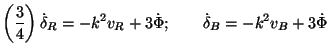(135)

The Euler equations, however, gets modified; for photons, it becomes:

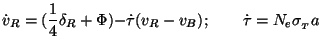(136)

The first two terms in the right hand side are exactly the same as the ones in Eq. (55). The last term is analogous to a viscous drag force between the photons and baryons which arises because of the non zero relative velocity between the two fluids. The coupling is essentially due to Thomson scattering which leads to the factor 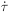. (The notation, and the physics, is the same as in Eq. (130)). The corresponding Euler equation for the baryons is:

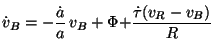(137)

where

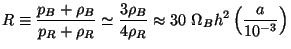(138)

Again, the first two terms in the right hand side of Eq. (137) are the same as what we had before in Eq. (55). The last term has the same interpretation as in the case of Euler equation Eq. (136) for photons, except for the factor R. This quantity essentially takes care of the inertia of baryons relative to photons. Note that the the conserved momentum density of photon-baryon fluid has the form

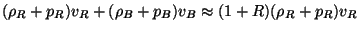(139)

which accounts for the extra factor R in Eq. (137).

We can now combine the Eqs. (135), (136), (137) to obtain, to lowest order in (k / 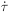) the equation:

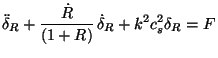(140)

with

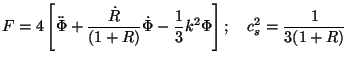(141)

An exact solution to this equation is difficult to obtain. However, we can try to understand several features by an approximate method in which we treat the time variation of R to be small. In that case, we can drop the terms on both sides of the equation. Since we know that the physically relevant temperature fluctuation is = (1/4)_R + , we can recast the above equation for as:

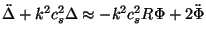(142)

Let us further ignore the time variation of all terms (especially on the right hand side). Then, the solution is just = -R + A cos(kc_{s LSS}) + Bsin(kc_{s LSS}). To fix the initial conditions which determine A and B, we recall that early on ( 0), we have /3 (see Eq. (115)) and corresponding velocity should vanish. This gives the solution:

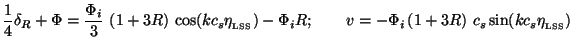(143)

(One can do a little better by using WKB approximation in which (kc_{s LSS}) can be replaced by the integral of kc_s over but it is not very important.) Given this solution, one can proceed as before and compute the C_l's. Adding the effects of [ + (1/4)_R] and that of [v · n] in quadrature and noticing that the angular average of <(v · n)²> = (1/3) v² we can estimate the C_l for scale invariant ( k³|_k|² = 2² A² ) spectrum to be:

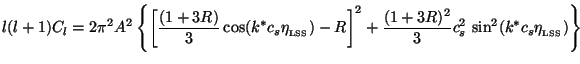(144)

with k^*L l with L = ₀ - _{LSS 0}. The key feature is, of course, the maxima and minima which arises from the trigonometric functions. The peaks of C_l are determined by the condition k^* c_{s LSS} = lc_{s LSS} / ₀ = n ; that is

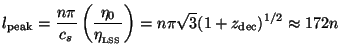(145)

More precise work gives the first peak at l_peak 200. It is also clear that because of non zero R the peaks are larger when the cosine term is negative; that is, the odd peaks corresponding to n= 1, 3, ... have larger amplitudes than the even peaks with n = 2, 4, ....

Incidentally, the above approximation is not very good for modes which enter the Hubble radius during the radiation dominated phase since does evolve with time (and decays) in the radiation dominated phase. We saw that -3_i (ly)^-2 cos(ly) asymptotically in this phase (see Eq. (80)). From Eq. (80) we find that during this phase, for modes which are inside the Hubble radius, we can take _R 6_i cos(ly), so that _R/4 (3/2)_i cos(ly). On the other hand, at very large scale, the amplitude was = /3 = (1/3)(9/10)_i = (3/10)_i. Hence the amplitude of the modes that enter the horizon during the radiation dominated phase is enhanced by a factor (3/2)(10/9) = 5, relative to the large scale amplitude contributed by modes which enter during matter dominated phase. This is essentially due to the driving term which is nonzero in the radiation dominated phase but zero in the matter dominated phase. (In reality, the enhancement is smaller because the relevant modes have k k_eq rather than k >> k_eq; see Figs. 3 and 4.)

If this were the whole story, we will see a series of peaks and troughs in the temperature anisotropies as a function of angular scale. In reality, however, there are processes which damp out the anisotropies at small angular scales (large -l) so that only the first few peaks and troughs are really relevant. We will now discuss two key damping mechanisms which are responsible for this.

The first one is the finite width of the last scattering surface which makes it uncertain from which event we are receiving the photons. In general, if 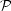(z) is the probability that the photon was last scattered at redshift z, then we can write:

(146)

From Eq. (41) we know that 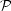(z) is a Gaussian with width z = 80. This corresponds to a length scale

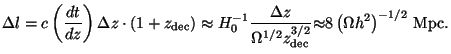(147)

over which the temperature fluctuations will be smoothed out.

It turns out that there is another effect, which is slightly more important. This arises from the fact that the photon-baryon fluid is not tightly coupled and the photons can diffuse through the fluid. This diffusion can be modeled as a random walk and the root mean square distance traveled by the photon during this diffusion process will smear the temperature anisotropies over that length scale. This photon diffusion length scale can be estimated as follows:

(148)

Integrating, we find the mean square distance traveled by the photon to be

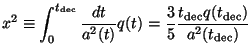(149)

The corresponding proper length scale below which photon diffusion will wipe out temperature anisotropies is:

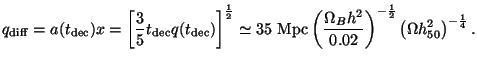(150)

It turns out that this is the dominant sources of damping of temperature anisotropies at large l 10³.