8. THE DARK ENERGY

It is rather frustrating that the only component of the universe which we understand theoretically is the radiation! While understanding the baryonic and dark matter components [in particular the values of _B and _DM] is by no means trivial, the issue of dark energy is lot more perplexing, thereby justifying the attention it has received recently. In this section we will discuss several aspects of the dark energy problem.

The key observational feature of dark energy is that - treated as a fluid with a stress tensor T_b^a = dia (, -p, -p, -p) - it has an equation state p = w with w -0.8 at the present epoch. The spatial part g of the geodesic acceleration (which measures the relative acceleration of two geodesics in the spacetime) satisfies an exact equation in general relativity given by:

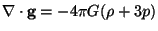(190)

This shows that the source of geodesic acceleration is ( + 3p) and not . As long as ( + 3p) > 0, gravity remains attractive while ( + 3p) < 0 can lead to repulsive gravitational effects. In other words, dark energy with sufficiently negative pressure will accelerate the expansion of the universe, once it starts dominating over the normal matter. This is precisely what is established from the study of high redshift supernova, which can be used to determine the expansion rate of the universe in the past [6].

The simplest model for a fluid with negative pressure is the cosmological constant (for some recent reviews, see [23]) with w = -1, = -p = constant. If the dark energy is indeed a cosmological constant, then it introduces a fundamental length scale in the theory L H^-1, related to the constant dark energy density _DE by H² (8 G _DE / 3). In classical general relativity, based on the constants G, c and L, it is not possible to construct any dimensionless combination from these constants. But when one introduces the Planck constant, , it is possible to form the dimensionless combination H²(G / c³) (L_p² / L²). Observations then require (L_p² / L²) 10^-123. As has been mentioned several times in literature, this will require enormous fine tuning. What is more, in the past, the energy density of normal matter and radiation would have been higher while the energy density contributed by the cosmological constant does not change. Hence we need to adjust the energy densities of normal matter and cosmological constant in the early epoch very carefully so that _NR around the current epoch. This raises the second of the two cosmological constant problems: Why is it that ( / _NR) = (1) at the current phase of the universe ?

Because of these conceptual problems associated with the cosmological constant, people have explored a large variety of alternative possibilities. The most popular among them uses a scalar field with a suitably chosen potential V() so as to make the vacuum energy vary with time. The hope then is that, one can find a model in which the current value can be explained naturally without any fine tuning. A simple form of the source with variable w are scalar fields with Lagrangians of different forms, of which we will discuss two possibilities:

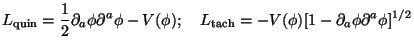(191)

Both these Lagrangians involve one arbitrary function V(). The first one, L_quin, which is a natural generalization of the Lagrangian for a non-relativistic particle, L = (1/2) ² - V(q), is usually called quintessence (for a small sample of models, see [24]; there is an extensive and growing literature on scalar field models and more references can be found in the reviews in ref. [23]). When it acts as a source in Friedmann universe, it is characterized by a time dependent w(t) with

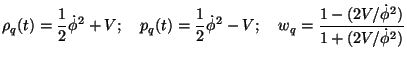(192)

The structure of the second Lagrangian (which arise in string theory [25]) in Eq. (191) can be understood by a simple analogy from special relativity. A relativistic particle with (one dimensional) position q(t) and mass m is described by the Lagrangian L = -m (1 - ²)^1/2. It has the energy E = m / (1 - ²)^1/2 and momentum k = m / (1 - ²)^1/2 which are related by E² = k² + m². As is well known, this allows the possibility of having massless particles with finite energy for which E² = k². This is achieved by taking the limit of m 0 and 1, while keeping the ratio in E = m / (1 - ²)^1/2 finite. The momentum acquires a life of its own, unconnected with the velocity , and the energy is expressed in terms of the momentum (rather than in terms of ) in the Hamiltonian formulation. We can now construct a field theory by upgrading q(t) to a field . Relativistic invariance now requires to depend on both space and time [ = (t, x)] and ² to be replaced by _i ⁱ . It is also possible now to treat the mass parameter m as a function of , say, V() thereby obtaining a field theoretic Lagrangian L = -V() (1 - ⁱ _i )^1/2. The Hamiltonian structure of this theory is algebraically very similar to the special relativistic example we started with. In particular, the theory allows solutions in which V 0, _i ⁱ 1 simultaneously, keeping the energy (density) finite. Such solutions will have finite momentum density (analogous to a massless particle with finite momentum k) and energy density. Since the solutions can now depend on both space and time (unlike the special relativistic example in which q depended only on time), the momentum density can be an arbitrary function of the spatial coordinate. The structure of this Lagrangian is similar to those analyzed in a wide class of models called K-essence [26] and provides a rich gamut of possibilities in the context of cosmology [27^, 28].

Since the quintessence field (or the tachyonic field) has an undetermined free function V(), it is possible to choose this function in order to produce a given H(a). To see this explicitly, let us assume that the universe has two forms of energy density with (a) = _known(a) + (a) where _known(a) arises from any known forms of source (matter, radiation, ...) and (a) is due to a scalar field. Let us first consider quintessence. Here, the potential is given implicitly by the form [29, 27].

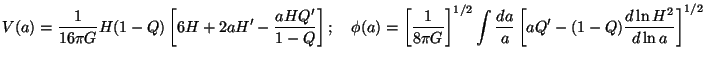(193)

where Q(a) [8 G _known(a) / 3H²(a)] and prime denotes differentiation with respect to a. (The result used in Eq. (155) is just a special case of this when Q = 0) Given any H(a), Q(a), these equations determine V(a) and (a) and thus the potential V(). Every quintessence model studied in the literature can be obtained from these equations.

Similar results exists for the tachyonic scalar field as well [27]. For example, given any H(a), one can construct a tachyonic potential V() so that the scalar field is the source for the cosmology. The equations determining V() are now given by:

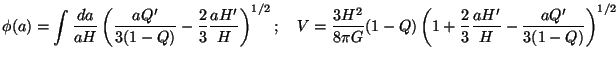(194)

Equations (194) completely solve the problem. Given any H(a), these equations determine V(a) and (a) and thus the potential V(). A wide variety of phenomenological models with time dependent cosmological constant have been considered in the literature all of which can be mapped to a scalar field model with a suitable V().

While the scalar field models enjoy considerable popularity (one reason being they are easy to construct!) it is very doubtful whether they have helped us to understand the nature of the dark energy at any deeper level. These models, viewed objectively, suffer from several shortcomings:

• They completely lack predictive power. As explicitly demonstrated above, virtually every form of a(t) can be modeled by a suitable "designer" V().

• These models are degenerate in another sense. The previous discussion illustrates that even when w(a) is known/specified, it is not possible to proceed further and determine the nature of the scalar field Lagrangian. The explicit examples given above show that there are at least two different forms of scalar field Lagrangians (corresponding to the quintessence or the tachyonic field) which could lead to the same w(a). (See the second paper in ref. [7] for an explicit example of such a construction.)

• All the scalar field potentials require fine tuning of the parameters in order to be viable. This is obvious in the quintessence models in which adding a constant to the potential is the same as invoking a cosmological constant. So to make the quintessence models work, we first need to assume the cosmological constant is zero. These models, therefore, merely push the cosmological constant problem to another level, making it somebody else's problem!.

• By and large, the potentials used in the literature have no natural field theoretical justification. All of them are non-renormalisable in the conventional sense and have to be interpreted as a low energy effective potential in an ad hoc manner.

• One key difference between cosmological constant and scalar field models is that the latter lead to a w(a) which varies with time. If observations have demanded this, or even if observations have ruled out w = -1 at the present epoch, then one would have been forced to take alternative models seriously. However, all available observations are consistent with cosmological constant (w = -1) and - in fact - the possible variation of w is strongly constrained [30] as shown in Figure 6.

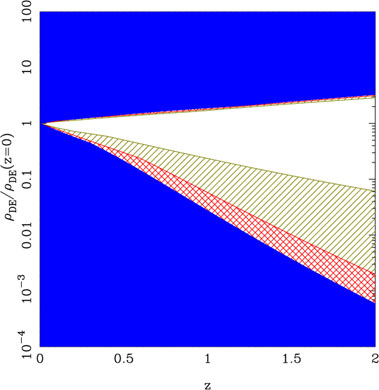Figure 6. The observational constraints on the variation of dark energy density as a function of redshift from WMAP and SNLS data (see [30]). The green/hatched region is excluded at 68% confidence limit, red/cross-hatched region at 95% confidence level and the blue/solid region at 99% confidence limit. The white region shows the allowed range of variation of dark energy at 68% confidence limit.

• While on the topic of observational constraints on w(t), it must be stressed that: (a) There is fair amount of tension between WMAP and SN data and one should be very careful about the priors used in these analysis. (b) There is no observational evidence for w < -1. (c) It is likely that more homogeneous, future, data sets of SN might show better agreement with WMAP results. (For more details related to these issues, see the last reference in [30].)

The observational and theoretical features described above suggests that one should consider cosmological constant as the most natural candidate for dark energy. Though it leads to well know fine tuning problems, it also has certain attractive features that need to kept in mind.

• Cosmological constant is the most economical [just one number] and simplest explanation for all the observations. We stress that there is absolutely no evidence for variation of dark energy density with redshift, which is consistent with the assumption of cosmological constant.

• Once we invoke the cosmological constant classical gravity will be described by the three constants G,c and L^-2. It is not possible to obtain a dimensionless quantity from these; so, within classical theory, there is no fine tuning issue. Since (G / c³) (L_p / L)² 10^-123, it is obvious that the cosmological constant is telling us something regarding quantum gravity, indicated by the combination G. An acid test for any quantum gravity model will be its ability to explain this value; needless to say, all the currently available models - strings, loops etc. - flunk this test.

• So, if dark energy is indeed cosmological constant, this will be the greatest contribution from cosmology to fundamental physics. It will be unfortunate if we miss this chance by invoking some scalar field epicycles!

In this context, it is worth stressing another peculiar feature of cosmological constant, when it is treated as a clue to quantum gravity. It is well known that, based on energy scales, the cosmological constant problem is an infra red problem par excellence. At the same time, it is a relic of a quantum gravitational effect or principle of unknown nature. An analogy [31] will be helpful to illustrate this point. Suppose one solves the Schrodinger equation for the Helium atom for the quantum states of the two electrons (x₁, x₂). When the result is compared with observations, one will find that only half the states - those in which (x₁, x₂) is antisymmetric under x₁ x₂ interchange - are realized in nature. But the low energy Hamiltonian for electrons in the Helium atom has no information about this effect! Here is low energy (IR) effect which is a relic of relativistic quantum field theory (spin-statistics theorem) that is totally non perturbative, in the sense that writing corrections to the Helium atom Hamiltonian in some (1 / c) expansion will not reproduce this result. The current value of cosmological constant could very well be related to quantum gravity in a similar way. There must exist a deep principle in quantum gravity which leaves its non perturbative trace even in the low energy limit that appears as the cosmological constant .

Let us now turn our attention to few of the many attempts to understand the cosmological constant. The choice is, of course, dictated by personal bias and is definitely a non-representative sample. A host of other approaches exist in literature, some of which can be found in [32].

8.1. Gravitational Holography

One possible way of addressing this issue is to simply eliminate from the gravitational theory those modes which couple to cosmological constant. If, for example, we have a theory in which the source of gravity is ( + p) rather than ( + 3p) in Eq. (190), then cosmological constant will not couple to gravity at all. (The non linear coupling of matter with gravity has several subtleties; see eg. [33].) Unfortunately it is not possible to develop a covariant theory of gravity using ( + p) as the source. But we can probably gain some insight from the following considerations. Any metric g_ab can be expressed in the form g_ab = f²(x) q_ab such that det q = 1 so that det g = f⁴. From the action functional for gravity

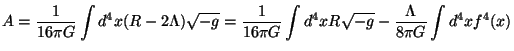(195)

it is obvious that the cosmological constant couples only to the conformal factor f. So if we consider a theory of gravity in which f⁴ = (-g)^1/2 is kept constant and only q_ab is varied, then such a model will be oblivious of direct coupling to cosmological constant. If the action (without the term) is varied, keeping det g = -1, say, then one is lead to a unimodular theory of gravity that has the equations of motion R_ab - (1/4)g_ab R = (T_ab - (1/4)g_ab T) with zero trace on both sides. Using the Bianchi identity, it is now easy to show that this is equivalent to the usual theory with an arbitrary cosmological constant. That is, cosmological constant arises as an undetermined integration constant in this model [34].

The same result arises in another, completely different approach to gravity. In the standard approach to gravity one uses the Einstein-Hilbert Lagrangian L_EH R which has a formal structure L_EH ~ R ~ ( g)² + ² g. If the surface term obtained by integrating L_sur ²g is ignored (or, more formally, canceled by an extrinsic curvature term) then the Einstein's equations arise from the variation of the bulk term L_bulk (g)² which is the non-covariant ² Lagrangian. There is, however, a remarkable relation between L_bulk and L_sur:

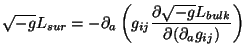(196)

which allows a dual description of gravity using either L_bulk or L_sur! It is possible to obtain the dynamics of gravity [35] from an approach which uses only the surface term of the Hilbert action; we do not need the bulk term at all!. This suggests that the true degrees of freedom of gravity for a volume reside in its boundary - a point of view that is strongly supported by the study of horizon entropy, which shows that the degrees of freedom hidden by a horizon scales as the area and not as the volume. The resulting equations can be cast in a thermodynamic form TdS = dE + PdV and the continuum spacetime is like an elastic solid (see e.g. [36]) with Einstein's equations providing the macroscopic description. Interestingly, the cosmological constant arises again in this approach as a undetermined integration constant but closely related to the `bulk expansion' of the solid.

While this is all very interesting, we still need an extra physical principle to fix the value (even the sign) of cosmological constant. One possible way of doing this is to interpret the term in the action as a Lagrange multiplier for the proper volume of the spacetime. Then it is reasonable to choose the cosmological constant such that the total proper volume of the universe is equal to a specified number. While this will lead to a cosmological constant which has the correct order of magnitude, it has several obvious problems. First, the proper four volume of the universe is infinite unless we make the spatial sections compact and restrict the range of time integration. Second, this will lead to a dark energy density which varies as t^-2 (corresponding to w = -1/3 ) which is ruled out by observations.

8.2. Cosmic Lenz law

Another possibility which has been attempted in the literature tries to "cancel out" the cosmological constant by some process, usually quantum mechanical in origin. One of the simplest ideas will be to ask whether switching on a cosmological constant will lead to a vacuum polarization with an effective energy momentum tensor that will tend to cancel out the cosmological constant. A less subtle way of doing this is to invoke another scalar field (here we go again!) such that it can couple to cosmological constant and reduce its effective value [37]. Unfortunately, none of this could be made to work properly. By and large, these approaches lead to an energy density which is either _UV L_p^-4 (where L_p is the Planck length) or to _IR L^-4 (where L = H^-1 is the Hubble radius associated with the cosmological constant ). The first one is too large while the second one is too small!

8.3. Geometrical Duality in our Universe

While the above ideas do not work, it gives us a clue. A universe with two length scales L and L_p will be asymptotically De Sitter with a(t) exp(t / L) at late times. There are some curious features in such a universe which we will now describe. Given the two length scales L_p and L, one can construct two energy scales _UV = 1 / L_p⁴ and _IR = 1 / L⁴ in natural units (c = = 1). There is sufficient amount of justification from different theoretical perspectives to treat L_p as the zero point length of spacetime [38], giving a natural interpretation to _UV. The second one, _IR also has a natural interpretation. The universe which is asymptotically De Sitter has a horizon and associated thermodynamics [39] with a temperature T = H / 2 and the corresponding thermal energy density _thermal T⁴ 1 / L⁴ = _IR. Thus L_p determines the highest possible energy density in the universe while L determines the lowest possible energy density in this universe. As the energy density of normal matter drops below this value, the thermal ambience of the De Sitter phase will remain constant and provide the irreducible `vacuum noise'. Note that the dark energy density is the the geometric mean _DE = (_{IR UV})^1/2 between the two energy densities. If we define a dark energy length scale L_DE such that _DE = 1 / L_DE⁴ then L_DE = (L_P L)^1/2 is the geometric mean of the two length scales in the universe. (Incidentally, L_DE 0.04 mm is macroscopic; it is also pretty close to the length scale associated with a neutrino mass of 10^-2 eV; another intriguing coincidence ?!)

Using the characteristic length scale of expansion, the Hubble radius d_H ( / a)^-1, we can distinguish between three different phases of such a universe. The first phase is when the universe went through a inflationary expansion with d_H = constant; the second phase is the radiation/matter dominated phase in which most of the standard cosmology operates and d_H increases monotonically; the third phase is that of re-inflation (or accelerated expansion) governed by the cosmological constant in which d_H is again a constant. The first and last phases are time translation invariant; that is, t t + constant is an (approximate) invariance for the universe in these two phases. The universe satisfies the perfect cosmological principle and is in steady state during these phases!

In fact, one can easily imagine a scenario in which the two De Sitter phases (first and last) are of arbitrarily long duration [40]. If 0.7, _DM 0.3 the final De Sitter phase does last forever; as regards the inflationary phase, nothing prevents it from lasting for arbitrarily long duration. Viewed from this perspective, the in between phase - in which most of the `interesting' cosmological phenomena occur - is of negligible measure in the span of time. It merely connects two steady state phases of the universe.

While the two De Sitter phases can last forever in principle, there is a natural cut off length scale in both of them which makes the region of physical relevance to be finite [40]. Let us first discuss the case of re-inflation in the late universe. As the universe grows exponentially in the phase 3, the wavelength of CMBR photons are being redshifted rapidly. When the temperature of the CMBR radiation drops below the De Sitter temperature (which happens when the wavelength of the typical CMBR photon is stretched to the L.) the universe will be essentially dominated by the vacuum thermal noise [39] due to the horizon in the De Sitter phase. This happens when the expansion factor is a = a_f determined by the equation T₀ (a₀ / a_f) = (1/2 L). Let a = a be the epoch at which cosmological constant started dominating over matter, so that (a / a₀)³ = (_DM / ). Then we find that the dynamic range of the phase 3 is

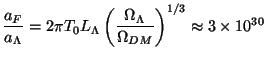(197)

Interestingly enough, one can also impose a similar bound on the physically relevant duration of inflation. We know that the quantum fluctuations, generated during this inflationary phase, could act as seeds of structure formation in the universe. Consider a perturbation at some given wavelength scale which is stretched with the expansion of the universe as a(t). During the inflationary phase, the Hubble radius remains constant while the wavelength increases, so that the perturbation will `exit' the Hubble radius at some time. In the radiation dominated phase, the Hubble radius d<sub>H</sub> t a<sup>2</sup> grows faster than the wavelength a(t). Hence, normally, the perturbation will `re-enter' the Hubble radius at some time. If there was no re-inflation, all wavelengths will re-enter the Hubble radius sooner or later. But if the universe undergoes re-inflation, then the Hubble radius `flattens out' at late times and some of the perturbations will never reenter the Hubble radius ! If we use the criterion that we need the perturbation to reenter the Hubble radius, we get a natural bound on the duration of inflation which is of direct astrophysical relevance. Consider a perturbation which leaves the Hubble radius (H_in^-1) during the inflationary epoch at a = a_i. It will grow to the size H_in^-1(a / a_i) at a later epoch. We want to determine a_i such that this length scale grows to L just when the dark energy starts dominating over matter; that is at the epoch a = a = a₀(_DM / )^1/3. This gives H_in^-1(a / a_i) = L so that a_i = (H_in^-1 / L)(_DM / )^1/3 a₀. On the other hand, the inflation ends at a = a_end where a_end / a₀ = T₀ / T_reheat where T_reheat is the temperature to which the universe has been reheated at the end of inflation. Using these two results we can determine the dynamic range of this phase 1 to be

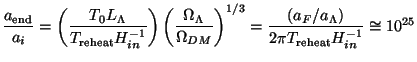(198)

where we have used the fact that, for a GUTs scale inflation with E_GUT = 10¹⁴ GeV, T_reheat = E_GUT, _in = E_GUT⁴ we have 2 H_in^-1 T_reheat = (3 / 2)^1/2(E_p / E_GUT) 10⁵. If we consider a quantum gravitational, Planck scale, inflation with 2 H_in^-1 T_reheat = (1), the ranges in Eq. (197) and Eq. (198) are approximately equal.

This fact is definitely telling us something regarding the duality between Planck scale and Hubble scale or between the infrared and ultraviolet limits of the theory. The mystery is compounded by the fact the asymptotic De Sitter phase has an observer dependent horizon and related thermal properties [39]. Recently, it has been shown - in a series of papers, see ref. [35] - that it is possible to obtain classical relativity from purely thermodynamic considerations. It is difficult to imagine that these features are unconnected and accidental; at the same time, it is difficult to prove a definite connection between these ideas and the cosmological constant.

8.4. Gravity as detector of the vacuum energy

Finally, we will describe an idea which does lead to the correct value of cosmological constant. The conventional discussion of the relation between cosmological constant and vacuum energy density is based on evaluating the zero point energy of quantum fields with an ultraviolet cutoff and using the result as a source of gravity. Any reasonable cutoff will lead to a vacuum energy density _vac which is unacceptably high. This argument, however, is too simplistic since the zero point energy - obtained by summing over the (1/2) _k - has no observable consequence in any other phenomena and can be subtracted out by redefining the Hamiltonian. The observed non trivial features of the vacuum state of QED, for example, arise from the fluctuations (or modifications) of this vacuum energy rather than the vacuum energy itself. This was, in fact, known fairly early in the history of cosmological constant problem and is stressed by Zeldovich [41] who explicitly calculated one possible contribution to fluctuations after subtracting away the mean value. This suggests that we should consider the fluctuations in the vacuum energy density in addressing the cosmological constant problem.

If the vacuum probed by the gravity can readjust to take away the bulk energy density _UV L_p^-4, quantum fluctuations can generate the observed value _DE. One of the simplest models [42] which achieves this uses the fact that, in the semi-classical limit, the wave function describing the universe of proper four-volume will vary as exp(-iA₀) exp[ -i(_eff / L_p²)]. If we treat ( / L_p², ) as conjugate variables then uncertainty principle suggests L_p² / . If the four volume is built out of Planck scale substructures, giving = NL_p⁴, then the Poisson fluctuations will lead to ^1/2 L_p² giving = L_p² / 1 / ^1/2 H₀² . (This idea can be a more quantitative; see [42]).

Similar viewpoint arises, more rigorously, when we study the question of detecting the energy density using gravitational field as a probe. Recall that an Unruh-DeWitt detector with a local coupling L_I = M() [x()] to the field actually responds to <0|(x)(y)|0> rather than to the field itself [43]. Similarly, one can use the gravitational field as a natural "detector" of energy momentum tensor T_ab with the standard coupling L = h_ab T^ab. Such a model was analysed in detail in ref. [44] and it was shown that the gravitational field responds to the two point function ⟨ 0|T_ab(x) T_cd(y)|0⟩ . In fact, it is essentially this fluctuations in the energy density which is computed in the inflationary models (see Eq. (170)) as the seed source for gravitational field, as stressed in ref. [11]. All these suggest treating the energy fluctuations as the physical quantity "detected" by gravity, when one needs to incorporate quantum effects. If the cosmological constant arises due to the energy density of the vacuum, then one needs to understand the structure of the quantum vacuum at cosmological scales. Quantum theory, especially the paradigm of renormalization group has taught us that the energy density - and even the concept of the vacuum state - depends on the scale at which it is probed. The vacuum state which we use to study the lattice vibrations in a solid, say, is not the same as vacuum state of the QED.

In fact, it seems inevitable that in a universe with two length scale L, L_p, the vacuum fluctuations will contribute an energy density of the correct order of magnitude _DE = (_{IR UV})^1/2. The hierarchy of energy scales in such a universe, as detected by the gravitational field has [40, 45] the pattern

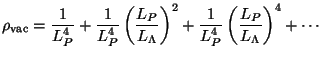(199)

The first term is the bulk energy density which needs to be renormalized away (by a process which we do not understand at present); the third term is just the thermal energy density of the De Sitter vacuum state; what is interesting is that quantum fluctuations in the matter fields inevitably generate the second term.

The key new ingredient arises from the fact that the properties of the vacuum state depends on the scale at which it is probed and it is not appropriate to ask questions without specifying this scale. If the spacetime has a cosmological horizon which blocks information, the natural scale is provided by the size of the horizon, L, and we should use observables defined within the accessible region. The operator H(< L), corresponding to the total energy inside a region bounded by a cosmological horizon, will exhibit fluctuations E since vacuum state is not an eigenstate of this operator. The corresponding fluctuations in the energy density, ( E) /L³ = f(L_p, L) will now depend on both the ultraviolet cutoff L_p as well as L. To obtain _vac E / L³ which scales as (L_p L)^-2 we need to have ( E)² L_p^-4 L²; that is, the square of the energy fluctuations should scale as the surface area of the bounding surface which is provided by the cosmic horizon. Remarkably enough, a rigorous calculation [45] of the dispersion in the energy shows that for L >> L_p, the final result indeed has the scaling

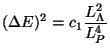(200)

where the constant c₁ depends on the manner in which ultra violet cutoff is imposed. Similar calculations have been done (with a completely different motivation, in the context of entanglement entropy) by several people and it is known that the area scaling found in Eq. (200), proportional to L², is a generic feature [46]. For a simple exponential UV-cutoff, c₁ = (1/30²) but cannot be computed reliably without knowing the full theory. We thus find that the fluctuations in the energy density of the vacuum in a sphere of radius L is given by

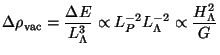(201)

The numerical coefficient will depend on c₁ as well as the precise nature of infrared cutoff radius (like whether it is L or L / 2 etc.). It would be pretentious to cook up the factors to obtain the observed value for dark energy density. But it is a fact of life that a fluctuation of magnitude _vac H² / G will exist in the energy density inside a sphere of radius H^-1 if Planck length is the UV cut off. One cannot get away from it. On the other hand, observations suggest that there is a _vac of similar magnitude in the universe. It seems natural to identify the two, after subtracting out the mean value by hand. Our approach explains why there is a surviving cosmological constant which satisfies _DE = (_{IR UV})^1/2 which - in our opinion - is the problem.

Acknowledgement

I thank J. Alcaniz for his friendship and warm hospitality during the X Special Courses at Observatorio Nacional, Rio de Janeiro, Brazil and for persuading me to write up my lecture notes. I am grateful to Gaurang Mahajan for help in generating the figures.