


In the description of linear perturbation theory given above, we assumed that some small perturbations existed in the early universe which are amplified through gravitational instability. To provide a complete picture we need a mechanism for generation of these initial perturbations. One such mechanism is provided by inflationary scenario which allows for the quantum fluctuations in the field driving the inflation to provide classical energy density perturbations at a late epoch. (Originally inflationary scenarios were suggested as pseudo-solutions to certain pseudo-problems; that is only of historical interest today and the only reason to take the possibility of an inflationary phase in the early universe seriously is because it provides a mechanism for generating these perturbations.) We shall now discuss how this can come about.
The basic assumption in inflationary scenario is that the universe underwent a rapid - nearly exponential - expansion for a brief period of time in very early universe. The simplest way of realizing such a phase is to postulate the existence of a scalar field with a nearly flat potential. The dynamics of the universe, driven by a scalar field source, is described by:
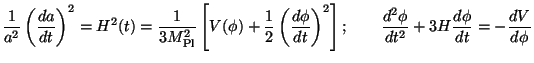 |
(151) |
where Mpl =
(8 G)-1/2.
If the potential is nearly flat for certain range of
G)-1/2.
If the potential is nearly flat for certain range of
 , we can
introduce the
" slow roll-over" approximation, under which these equations become:
, we can
introduce the
" slow roll-over" approximation, under which these equations become:
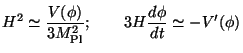 |
(152) |
For this slow roll-over to last for reasonable length of time, we need to assume that the terms ignored in the Eq. (151) are indeed small. This can be quantified in terms of the parameters:
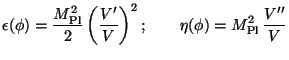 |
(153) |
which are taken to be small. Typically the inflation ends when this assumption breaks down. If such an inflationary phase lasts up to some time tend then the universe would have undergone an expansion by a factor expN(t) during the interval (t, tend) where
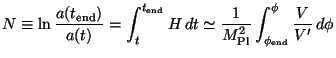 |
(154) |
One usually takes N
 65 or so.
65 or so.
Before proceeding further, we would like to make couple of comments
regarding such an inflationary phase. To begin with, it is not
difficult to obtain exact solutions for a(t) with rapid
expansion by tailoring the potential for the scalar field. In fact,
given any a(t) and thus a H(t) =
( / a), one can
determine a potential
V(
/ a), one can
determine a potential
V( ) for
a scalar field such that Eq. (151) are
satisfied (see the first reference in
[27]).
One can verify that, this is done by the choice:
) for
a scalar field such that Eq. (151) are
satisfied (see the first reference in
[27]).
One can verify that, this is done by the choice:
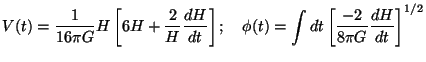 |
(155) |
Given any H(t), these equations give
( (t),
V(t)) and thus implicitly determine the necessary
V(
(t),
V(t)) and thus implicitly determine the necessary
V( ). As
an example, note that
a power law inflation, a(t) =
a0 t p (with p
>> 1) is generated by:
). As
an example, note that
a power law inflation, a(t) =
a0 t p (with p
>> 1) is generated by:
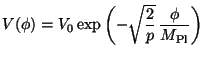 |
(156) |
while an exponential of power law
 |
(157) |
can arise from
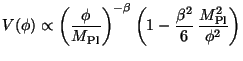 |
(158) |
Thus generating a rapid expansion in the early universe is trivial if we are willing to postulate scalar fields with tailor made potentials. This is often done in the literature.
The second point to note regarding any inflationary scenarios is that
the modes with reasonable size today originated from sub-Planck length
scales early on. A scale
 0 today will be
0 today will be
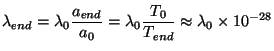 |
(159) |
at the end of inflation (if inflation took place at GUT scales) and
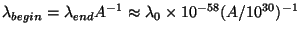 |
(160) |
at the beginning of inflation if the inflation changed the scale factor
by A  1030. Note that
1030. Note that
 begin
< Lp for
begin
< Lp for
 0 <3
Mpc!! Most structures in the universe today correspond to transplanckian
scales at the start of the inflation. It is not clear whether we can
trust standard physics at early stages of inflation or whether
transplanckian effects will lead to observable effects
[20,
21].
0 <3
Mpc!! Most structures in the universe today correspond to transplanckian
scales at the start of the inflation. It is not clear whether we can
trust standard physics at early stages of inflation or whether
transplanckian effects will lead to observable effects
[20,
21].
Let us get back to conventional wisdom and consider the evolution of
perturbations in a universe which underwent exponential
inflation. During the inflationary phase the a(t) grows
exponentially
and hence the wavelength of any perturbation will also grow with it. The
Hubble radius, on the other hand, will remain constant. It follows that,
one can have situation in which a given mode has wavelength smaller than
the Hubble radius at the beginning of the inflation but grows and
becomes bigger than the Hubble radius as inflation proceeds. It is
conventional to say that a perturbation of comoving wavelength
 0 "leaves
the Hubble radius" when
0 "leaves
the Hubble radius" when
 0 a
= dH at some time t =
texit(
0 a
= dH at some time t =
texit( 0). For t > texit
the wavelength of the
perturbation is bigger than the Hubble radius. Eventually the inflation
ends and the universe becomes radiation dominated. Then the wavelength
will grow (
0). For t > texit
the wavelength of the
perturbation is bigger than the Hubble radius. Eventually the inflation
ends and the universe becomes radiation dominated. Then the wavelength
will grow ( t1/2) slower than the Hubble radius
(
t1/2) slower than the Hubble radius
( t) and will
enter the Hubble radius again during
t = tenter(
t) and will
enter the Hubble radius again during
t = tenter( 0). Our first task is to
relate the amplitude of the perturbation at t =
texit(
0). Our first task is to
relate the amplitude of the perturbation at t =
texit( 0) with
the perturbation at t = tenter(
0) with
the perturbation at t = tenter( 0).
0).
We know that for modes bigger than Hubble radius, we have the conserved quantity (see Eq. (97)
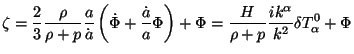 |
(161) |
At the time of re-entry, the universe is radiation dominated and
 entry
entry
 (2/3)
(2/3)  .
On the other hand, during inflation, we can write the scalar field as a
dominant homogeneous part plus a small, spatially varying fluctuation:
.
On the other hand, during inflation, we can write the scalar field as a
dominant homogeneous part plus a small, spatially varying fluctuation:
 (t,
x) =
(t,
x) =
 0(t) + f(t, x).
Perturbing the equation in Eq. (151) for the scalar field, we
find that the homogeneous mode
0(t) + f(t, x).
Perturbing the equation in Eq. (151) for the scalar field, we
find that the homogeneous mode
 0
satisfies Eq. (151) while
the perturbation, in Fourier space satisfies:
0
satisfies Eq. (151) while
the perturbation, in Fourier space satisfies:
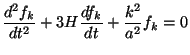 |
(162) |
Further, the energy momentum tensor for the scalar field gives
[with the "dot" denoting (d /
d ) =
a(d / dt)]:
) =
a(d / dt)]:
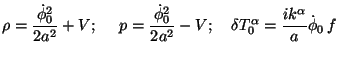 |
(163) |
It is easy to see that  is negligible at t = texit since
is negligible at t = texit since
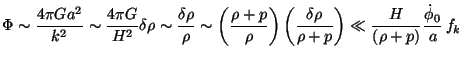 |
(164) |
Therefore,
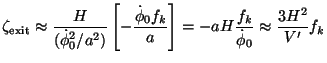 |
(165) |
Using the conservation law
 exit =
exit =
 entry, we get
entry, we get
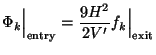 |
(166) |
Thus, given a perturbation of the scalar field fk during inflation, we can compute its value at the time of re-entry, which - in turn - can be used to compare with observations.
Equation (166) connects a classical energy density
perturbation fk at the time of exit with the
corresponding quantity
 k at the time
of re-entry. The next important - and
conceptually difficult - question is how we can obtain a
c-number field fk from a quantum scalar
field. There is no
simple answer to this question and one possible way of doing it is as
follows: Let us start with the quantum operator for a scalar field
decomposed into the Fourier modes with
qk(t) denoting an
infinite set of operators:
k at the time
of re-entry. The next important - and
conceptually difficult - question is how we can obtain a
c-number field fk from a quantum scalar
field. There is no
simple answer to this question and one possible way of doing it is as
follows: Let us start with the quantum operator for a scalar field
decomposed into the Fourier modes with
qk(t) denoting an
infinite set of operators:
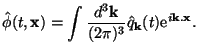 |
(167) |
We choose a quantum state
| > such the expectation
value of
> such the expectation
value of
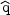 k(t) vanishes for all
non-zero k
so that the expectation value of
k(t) vanishes for all
non-zero k
so that the expectation value of
 (t,
x) gives the
homogeneous mode that drives the inflation. The quantum fluctuation
around this homogeneous part in a quantum state
|
(t,
x) gives the
homogeneous mode that drives the inflation. The quantum fluctuation
around this homogeneous part in a quantum state
| > is given by
> is given by
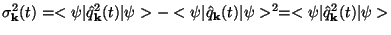 |
(168) |
It is easy to verify that this fluctuation is just the Fourier transform of the two-point function in this state:
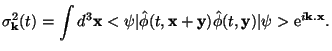 |
(169) |
Since  k
characterises the quantum fluctuations, it seems
reasonable to introduce a c-number field f(t, x) by
the definition:
k
characterises the quantum fluctuations, it seems
reasonable to introduce a c-number field f(t, x) by
the definition:
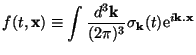 |
(170) |
This c-number field will have same c-number power spectrum as
the quantum fluctuations. Hence we may take this as our
definition of an equivalent classical perturbation. (There are more
sophisticated ways of getting this result but none of them are
fundamentally more sound that the elementary definition given
above. There is a large literature on the subject of quantum to
classical transition, especially in the context of gravity; see e.g.
[22])
We now have all the ingredients in place. Given the quantum state
| >, one can explicitly
compute
>, one can explicitly
compute
 k and
then - using
Eq. (166) with fk =
k and
then - using
Eq. (166) with fk =
 k -
obtain the density perturbations at the time of re-entry.
k -
obtain the density perturbations at the time of re-entry.
The next question we need to address is what is
| >. The free
quantum field theory in the Friedmann background is identical to the
quantum mechanics of a bunch of time dependent harmonic oscillators,
each labelled by a wave vector k.
The action for a free scalar field in the Friedmann background
>. The free
quantum field theory in the Friedmann background is identical to the
quantum mechanics of a bunch of time dependent harmonic oscillators,
each labelled by a wave vector k.
The action for a free scalar field in the Friedmann background
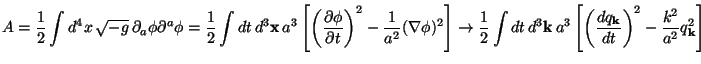 |
(171) |
can be thought of as the sum over the actions for an infinite set of
harmonic oscillators with
mass m = a3 and frequency
 k2
= k2 / a2. (To be precise, one
needs to treat the real and imaginary parts of the Fourier transform as
independent oscillators and restrict the range of k; just
pretending that qk is real amounts the same
thing.) The quantum state of the field is just an
infinite product of the quantum state
k2
= k2 / a2. (To be precise, one
needs to treat the real and imaginary parts of the Fourier transform as
independent oscillators and restrict the range of k; just
pretending that qk is real amounts the same
thing.) The quantum state of the field is just an
infinite product of the quantum state
 k[qk, t] for
each of the harmonic
oscillators and satisfies the Schrodinger equation
k[qk, t] for
each of the harmonic
oscillators and satisfies the Schrodinger equation
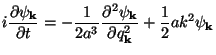 |
(172) |
If the quantum state  k[qk, t'] of
any given oscillator, labelled by k, is given at some initial
time, t', we can evolve it to final time:
k[qk, t'] of
any given oscillator, labelled by k, is given at some initial
time, t', we can evolve it to final time:
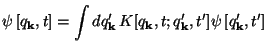 |
(173) |
where K is known in terms of the solutions to the classical
equations of motion and
 [qk',
t'] is the initial state.
There is nothing non-trivial in the mathematics, but the physics is
completely unknown. The real problem is that
unfortunately - in spite of confident assertions in the literature
occasionally - we have no clue what
[qk',
t'] is the initial state.
There is nothing non-trivial in the mathematics, but the physics is
completely unknown. The real problem is that
unfortunately - in spite of confident assertions in the literature
occasionally - we have no clue what
 [qk',
t'] is.
So we need to make more assumptions to proceed further.
[qk',
t'] is.
So we need to make more assumptions to proceed further.
One natural choice is the following: It turns out that, Gaussian states of the form
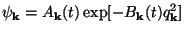 |
(174) |
preserve their form under evolution governed by the Schrodinger equation in Eq. (172). Substituting Eq. (174) in Eq. (172) we can determine the ordinary differential equation which governs Bk (t). (The Ak (t) is trivially fixed by normalization.) Simple algebra shows that Bk(t) can be expressed in the form
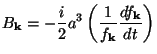 |
(175) |
where fk is the solution to the classical equation of motion:
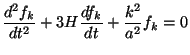 |
(176) |
For the quantum state in Eq. (174), the fluctuations are characterized by
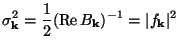 |
(177) |
Since one can take different choices for the solutions of
Eq. (176) one get different values for
 k and
different spectra for perturbations. Any prediction one makes depends
on the choice of mode functions. One possibility is to choose the modes
so that
k and
different spectra for perturbations. Any prediction one makes depends
on the choice of mode functions. One possibility is to choose the modes
so that  k
represents the instantaneous vacuum state of the
oscillators at some time t = ti.
(That is Re Bk(ti) =
(1/2)
k
represents the instantaneous vacuum state of the
oscillators at some time t = ti.
(That is Re Bk(ti) =
(1/2) k2(ti),
say). The final result will then depend on the choice for
ti. One can further make an
assumption that we are interested in the limit of ti
k2(ti),
say). The final result will then depend on the choice for
ti. One can further make an
assumption that we are interested in the limit of ti
 -
- ; that
is the quantum state is an instantaneous ground state in the infinite
past. It is easy to show that this corresponds to choosing the following
solution to Eq. (176):
; that
is the quantum state is an instantaneous ground state in the infinite
past. It is easy to show that this corresponds to choosing the following
solution to Eq. (176):
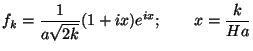 |
(178) |
which is usually called the Bunch-Davies vacuum. For this choice,
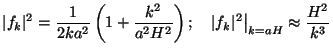 |
(179) |
where the second result is at t = texit which is what we need to use in Eq. (166), (Numerical factors of order unity cannot be trusted in this computation). We can now determine the amplitude of the perturbation when it re-enters the Hubble radius. Eq. (166) gives:
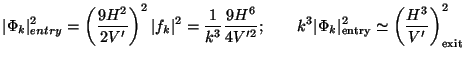 |
(180) |
One sees that the result is scale invariant in the sense that
k3| k|entry2 is independent of
k.
k|entry2 is independent of
k.
It is sometimes claimed in the literature that scale invariant spectrum
is a prediction of inflation. This is simply wrong. One has to
make several other assumptions including an all important
choice for the quantum state (about which we know nothing) to obtain
scale invariant spectrum. In fact, one can prove that, given any power
spectrum  (k),
one can find a quantum state such that this power spectrum is generated
(for an explicit construction, see the last reference in
[20]).
So whatever results are obtained by observations can be reconciled with
inflationary generation of perturbations.
(k),
one can find a quantum state such that this power spectrum is generated
(for an explicit construction, see the last reference in
[20]).
So whatever results are obtained by observations can be reconciled with
inflationary generation of perturbations.
To conclude the discussion, let us work out the perturbations for one
specific case. Let us consider the case of the

 4
model for which
4
model for which
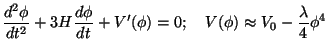 |
(181) |
Using
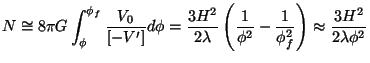 |
(182) |
we can write
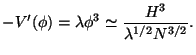 |
(183) |
so that the result in Eq. (180) becomes:
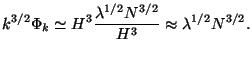 |
(184) |
We do get scale invariant spectrum but the amplitude has a serious
problem. If we take
N  50 and
note that observations require k3/2
50 and
note that observations require k3/2
 k ~
10-4 we need to take
k ~
10-4 we need to take

 10-15
for getting consistent values. Such a fine tuning of a dimensionless
coupling constant is fairly ridiculous; but over years inflationists
have learnt to successfully forget this embarrassment.
10-15
for getting consistent values. Such a fine tuning of a dimensionless
coupling constant is fairly ridiculous; but over years inflationists
have learnt to successfully forget this embarrassment.
Our formalism can also be used to estimate the deviation of the power spectrum from the scale invariant form. To the lowest order we have
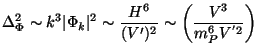 |
(185) |
Let us define the deviation from the scale invariant index by
(n - 1) = (d
ln
 2 /
d lnk). Using
2 /
d lnk). Using
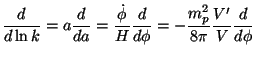 |
(186) |
one finds that
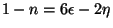 |
(187) |
Thus, as long as  and
and  are small
we do have n
are small
we do have n  1; what is more, given a potential one can estimate
1; what is more, given a potential one can estimate
 and
and
 and thus the
deviation (n-1).
and thus the
deviation (n-1).
Finally, note that the same process can also generate spin-2
perturbations. If we take the normalised gravity wave amplitude as
hab =
(16  G)1/2
eab
G)1/2
eab
 , the mode
function
, the mode
function  behaves like a scalar field.
(The normalisation is dictated by the fact that the action for the
perturbation should reduce to that of a spin-2 field.)
The corresponding power spectrum of gravity waves is
behaves like a scalar field.
(The normalisation is dictated by the fact that the action for the
perturbation should reduce to that of a spin-2 field.)
The corresponding power spectrum of gravity waves is
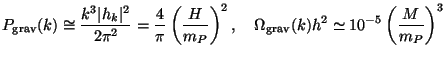 |
(188) |
Comparing the two results
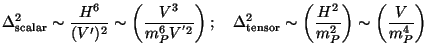 |
(189) |
we get
( tensor /
tensor /
 scalar)2
scalar)2
 16
16

 <<
1. Further, if (1 - n)
<<
1. Further, if (1 - n)
 4
4 (see Eq. (187) with
(see Eq. (187) with
 ~
~
 ) we have the
relation
(
) we have the
relation
( tensor
/
tensor
/  scalar)2
scalar)2

 (3)
(1 - n) which connects three quantities, all of which are
independently observable in principle. If these are actually measured in
future it could act as a consistency check of the inflationary paradigm.
(3)
(1 - n) which connects three quantities, all of which are
independently observable in principle. If these are actually measured in
future it could act as a consistency check of the inflationary paradigm.