


In this section, we provide a brief review of the elements of the FRW cosmological model. This model provides the context for interpreting the observational evidence for cosmic acceleration as well as the framework for understanding how cosmological probes in the future will help uncover the cause of acceleration by determining the history of the cosmic expansion with greater precision. For further details on basic cosmology, see, e.g., the textbooks of [Dodelson 2003, Kolb & Turner 1990, Peacock 1999], and [Peebles 1993]. Note that we follow the standard practice of using units in which the speed of light c = 1.
2.1. Friedmann-Robertson-Walker cosmology
From the large-scale distribution of galaxies and the near-uniformity of the CMB temperature, we have good evidence that the Universe is nearly homogeneous and isotropic. Under this assumption, the spacetime metric can be written in the FRW form,
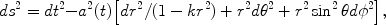 |
(1) |
where r,
 ,
,
 are comoving spatial
coordinates, t is time, and
the expansion is described by the cosmic scale factor,
a(t) (by convention, a = 1 today). The quantity
k is the curvature of 3-dimensional space: k = 0
corresponds to a spatially flat, Euclidean Universe, k > 0 to
positive curvature (3-sphere), and k < 0 to negative curvature
(saddle).
are comoving spatial
coordinates, t is time, and
the expansion is described by the cosmic scale factor,
a(t) (by convention, a = 1 today). The quantity
k is the curvature of 3-dimensional space: k = 0
corresponds to a spatially flat, Euclidean Universe, k > 0 to
positive curvature (3-sphere), and k < 0 to negative curvature
(saddle).
The wavelengths  of
photons moving through the Universe scale
with a(t), and the redshift of light emitted from a
distant source at time tem, 1 + z =
of
photons moving through the Universe scale
with a(t), and the redshift of light emitted from a
distant source at time tem, 1 + z =
 obs /
obs /
 em
=1/a(tem), directly reveals the relative
size of the Universe at that time. This means that time intervals are
related to redshift intervals by dt =
-dz / H(z)(1 + z), where H
em
=1/a(tem), directly reveals the relative
size of the Universe at that time. This means that time intervals are
related to redshift intervals by dt =
-dz / H(z)(1 + z), where H

 / a is the
Hubble parameter, and an overdot denotes a time
derivative. The present value of the Hubble parameter is conventionally
expressed as H0 = 100 h km/sec/Mpc, where
h
/ a is the
Hubble parameter, and an overdot denotes a time
derivative. The present value of the Hubble parameter is conventionally
expressed as H0 = 100 h km/sec/Mpc, where
h  0.7 is the
dimensionless Hubble parameter. Here and below, a subscript "0" on a
parameter denotes its value at the present epoch.
0.7 is the
dimensionless Hubble parameter. Here and below, a subscript "0" on a
parameter denotes its value at the present epoch.
The key equations of cosmology are the Friedmann equations, the field equations of GR applied to the FRW metric,
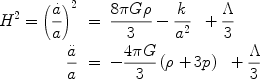 |
(2)
|
where  is the
total energy
density of the Universe (sum of matter, radiation, dark energy), and
p is the total pressure (sum of pressures of each component). For
historical reasons we display the cosmological constant
is the
total energy
density of the Universe (sum of matter, radiation, dark energy), and
p is the total pressure (sum of pressures of each component). For
historical reasons we display the cosmological constant
 here;
hereafter, we shall always represent it as vacuum energy and subsume it
into the density and pressure terms; the correspondence is:
here;
hereafter, we shall always represent it as vacuum energy and subsume it
into the density and pressure terms; the correspondence is:
 =
8
=
8 G
G
 VAC
= -8
VAC
= -8 G
pVAC.
G
pVAC.
For each component, the conservation of energy is expressed by
d(a3
 i ) =
-pi da3, the expanding
Universe analogue of the first law of thermodynamics,
dE = -pdV. Thus, the evolution of energy density is
controlled by the ratio of the pressure to the energy density, the
equation-of-state parameter, wi
i ) =
-pi da3, the expanding
Universe analogue of the first law of thermodynamics,
dE = -pdV. Thus, the evolution of energy density is
controlled by the ratio of the pressure to the energy density, the
equation-of-state parameter, wi
 pi
/
pi
/  i.
1 For the general case,
this ratio varies with time, and the evolution of the energy density in
a given component is given by
i.
1 For the general case,
this ratio varies with time, and the evolution of the energy density in
a given component is given by
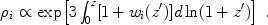 |
(4) |
In the case of constant wi,
 |
(5) |
For non-relativistic matter, which includes both dark matter and
baryons, wM = 0 to very good approximation, and
 M
M
 (1 +
z)3; for radiation, i.e., relativistic particles,
wR = 1/3, and
(1 +
z)3; for radiation, i.e., relativistic particles,
wR = 1/3, and
 R
R
 (1 +
z)4. For vacuum energy, as noted above
pVAC =
-
(1 +
z)4. For vacuum energy, as noted above
pVAC =
- VAC
= -
VAC
= - /
8
/
8 G = constant, i.e.,
wVAC = -1. For other models of dark energy, w
can differ from -1 and vary in time.
[Hereafter, w without a subscript refers to dark energy.]
G = constant, i.e.,
wVAC = -1. For other models of dark energy, w
can differ from -1 and vary in time.
[Hereafter, w without a subscript refers to dark energy.]
The present energy density of a flat Universe (k = 0),
 crit
crit
 3H02 /
8
3H02 /
8 G = 1.88 ×
10-29 h2 gm
cm-3 = 8.10 × 10-47
h2 GeV4, is known as the critical density;
it provides a convenient means of normalizing cosmic energy densities,
where
G = 1.88 ×
10-29 h2 gm
cm-3 = 8.10 × 10-47
h2 GeV4, is known as the critical density;
it provides a convenient means of normalizing cosmic energy densities,
where  i =
i =
 i(t0) /
i(t0) /
 crit.
For a positively curved Universe,
crit.
For a positively curved Universe,
 0
0

 (t0)
/
(t0)
/ crit
> 1 and for a negatively curved Universe
crit
> 1 and for a negatively curved Universe
 0 <
1. The present value of the curvature radius, Rcurv
0 <
1. The present value of the curvature radius, Rcurv
 a
/ (|k|)1/2, is related to
a
/ (|k|)1/2, is related to
 0 and
H0 by Rcurv =
H0-1 /
(|
0 and
H0 by Rcurv =
H0-1 /
(| 0
- 1|)1/2, and the
characteristic scale H0-1
0
- 1|)1/2, and the
characteristic scale H0-1
 3000 h-1 Mpc is known as the Hubble radius.
Because of the evidence from the CMB that the Universe is nearly
spatially flat (see Fig. 8), we shall assume k = 0 except where
otherwise noted.
3000 h-1 Mpc is known as the Hubble radius.
Because of the evidence from the CMB that the Universe is nearly
spatially flat (see Fig. 8), we shall assume k = 0 except where
otherwise noted.
Fig. 1
shows the evolution of the radiation, matter, and dark energy densities
with redshift. The Universe has gone through three distinct eras:
radiation-dominated, z
 3000;
matter-dominated, 3000
3000;
matter-dominated, 3000
 z
z
 0.5; and
dark-energy dominated, z
0.5; and
dark-energy dominated, z
 0.5. The
evolution of the scale factor is controlled by the
dominant energy form: a(t)
0.5. The
evolution of the scale factor is controlled by the
dominant energy form: a(t)
 t2/3(1 + w) (for constant w). During the
radiation-dominated era, a(t)
t2/3(1 + w) (for constant w). During the
radiation-dominated era, a(t)
 t1/2; during the matter-dominated era,
a(t)
t1/2; during the matter-dominated era,
a(t)  t2/3; and for the dark
energy-dominated era, assuming w = -1, asymptotically
a(t)
t2/3; and for the dark
energy-dominated era, assuming w = -1, asymptotically
a(t)  exp(Ht). For a flat Universe with
matter and vacuum energy, the general solution, which approaches the
latter two above at early and late times, is a(t)
= (
exp(Ht). For a flat Universe with
matter and vacuum energy, the general solution, which approaches the
latter two above at early and late times, is a(t)
= ( M
/
M
/  VAC)1/3
(sinh[3(
VAC)1/3
(sinh[3( VAC)1/2
H0 t / 2])2/3.
VAC)1/2
H0 t / 2])2/3.
 |
Figure 1. Evolution of radiation, matter, and dark energy densities with redshift. For dark energy, the band represents w = -1 ± 0.2. |
The deceleration parameter, q(z), is defined as
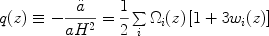 |
(6) |
where
 i(z)
i(z)

 i(z) /
i(z) /
 crit(z)
is the fraction of critical density in component i at redshift
z. During the matter- and radiation-dominated eras,
wi > 0 and gravity slows the expansion, so
that q > 0 and
crit(z)
is the fraction of critical density in component i at redshift
z. During the matter- and radiation-dominated eras,
wi > 0 and gravity slows the expansion, so
that q > 0 and
 < 0. Because of the
(
< 0. Because of the
( +
3p) term in the second Friedmann equation (Newtonian cosmology
would only have
+
3p) term in the second Friedmann equation (Newtonian cosmology
would only have
 ), the gravity
of a component that satisfies p <
-
), the gravity
of a component that satisfies p <
- / 3, i.e.,
w < -1/3, is repulsive and can cause the expansion to accelerate
(
/ 3, i.e.,
w < -1/3, is repulsive and can cause the expansion to accelerate
( > 0): we take this
to be the defining property of dark energy. The successful predictions
of the radiation-dominated era of cosmology, e.g., big bang
nucleosynthesis and the formation of CMB anisotropies, provide evidence
for the (
> 0): we take this
to be the defining property of dark energy. The successful predictions
of the radiation-dominated era of cosmology, e.g., big bang
nucleosynthesis and the formation of CMB anisotropies, provide evidence
for the ( +
3p) term, since during this epoch
+
3p) term, since during this epoch
 is
about twice as large as it would be in Newtonian cosmology.
is
about twice as large as it would be in Newtonian cosmology.
2.2. Distances and the Hubble diagram
For an object of intrinsic luminosity L, the measured energy flux F defines the luminosity distance dL to the object, i.e., the distance inferred from the inverse square law. The luminosity distance is related to the cosmological model through
 |
(7) |
where r(z) is the comoving distance to an object at redshift z,
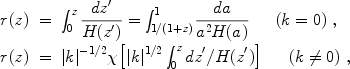 |
(8)
|
and where
 (x) =
sin(x) for k > 0 and
sinh(x) for k < 0. Specializing to the flat model and
constant w,
(x) =
sin(x) for k > 0 and
sinh(x) for k < 0. Specializing to the flat model and
constant w,
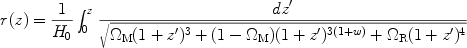 |
(10) |
where  M
is the present fraction of critical
density in non-relativistic matter, and
M
is the present fraction of critical
density in non-relativistic matter, and
 R
R
 0.8 ×
10-4 represents the small contribution to
the present energy density from photons and relativistic neutrinos. In
this model, the dependence of cosmic distances upon dark energy is
controlled by the parameters
0.8 ×
10-4 represents the small contribution to
the present energy density from photons and relativistic neutrinos. In
this model, the dependence of cosmic distances upon dark energy is
controlled by the parameters
 M and
w and
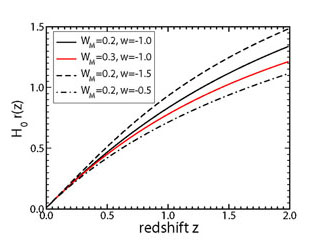
is shown in the left panel of Fig. 2.
M and
w and
is shown in the left panel of Fig. 2.
 |
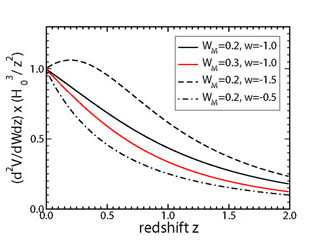 |
Figure 2. For a flat Universe,
the effect of dark energy upon cosmic distance (left) and volume element
(right) is controlled by
|
|
The luminosity distance is related to the distance modulus µ by
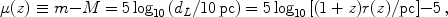 |
(11) |
where m is the apparent magnitude of the object (proportional to the log of the flux) and M is the the absolute magnitude (proportional to the log of the intrinsic luminosity). "Standard candles," objects of fixed absolute magnitude M, and measurements of the logarithmic energy flux m constrain the cosmological model and thereby the expansion history through this magnitude-redshift relation, known as the Hubble diagram.
Expanding the scale factor around its value today, a(t) = 1 + H0 (t - t0) - q0 H02 (t - t0)2 / 2 + ··· , the distance-redshift relation can be written in its historical form
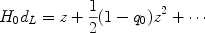 |
(12) |
The expansion rate and deceleration rate today appear in the first two terms in the Taylor expansion of the relation. This expansion, only valid for z << 1, is of historical significance and utility; it is not useful today since objects as distant as redshift z ~ 2 are being used to probe the expansion history. However, it does illustrate the general principle: the first term on the r.h.s. represents the linear Hubble expansion, and the deviation from a linear relation reveals the deceleration (or acceleration).
The angular-diameter distance dA, the distance
inferred from the angular size

 of a distant object of
fixed diameter D, is defined by dA
of a distant object of
fixed diameter D, is defined by dA
 D /
D /

 =
r(z) / (1 + z) = dL /
(1 + z)2. The
use of "standard rulers" (objects of fixed intrinsic size)
provides another means of probing the expansion history, again through
r(z).
=
r(z) / (1 + z) = dL /
(1 + z)2. The
use of "standard rulers" (objects of fixed intrinsic size)
provides another means of probing the expansion history, again through
r(z).
The cosmological time, or time back to the Big Bang, is given by
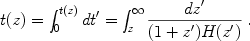 |
(13) |
While the present age in principle depends upon the expansion rate at
very early times, the rapid rise of H(z) with z
— a factor of 30,000 between today and the epoch of last
scattering, when photons and baryons decoupled, at
zLS  1100,
t(zLS)
1100,
t(zLS)
 380,000 years —
makes this point moot.
380,000 years —
makes this point moot.
Finally, the comoving volume element per unit solid angle
d is given by
is given by
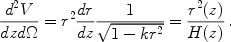 |
(14) |
For a set of objects of known comoving density n(z), the
comoving volume element can be used to infer
r2(z) / H(z) from the number counts
per unit redshift and solid angle, d2 N /
dzd =
n(z) d2 V /
dzd
=
n(z) d2 V /
dzd . The
dependence of the comoving volume element upon
. The
dependence of the comoving volume element upon
 M and
w is shown in the right panel of Fig. 2.
M and
w is shown in the right panel of Fig. 2.
2.3. Growth of structure and
 CDM
CDM
A striking success of the consensus cosmology
is its ability to account for the observed structure in the Universe,
provided that the dark matter is composed of slowly moving particles,
known as cold dark matter (CDM), and that the initial power spectrum of
density perturbations is nearly scale-invariant, P(k)
~ knS with spectral index
nS  1,
as predicted by inflation
[Springel, Frenk
& White 2006].
Dark energy affects the development of structure by
its influence on the expansion rate of the Universe when density
perturbations are growing. This fact and the quantity and quality of
large-scale structure data make structure formation a sensitive probe of
dark energy.
1,
as predicted by inflation
[Springel, Frenk
& White 2006].
Dark energy affects the development of structure by
its influence on the expansion rate of the Universe when density
perturbations are growing. This fact and the quantity and quality of
large-scale structure data make structure formation a sensitive probe of
dark energy.
In GR the growth of small-amplitude, matter-density perturbations on length scales much smaller than the Hubble radius is governed by
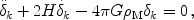 |
(15) |
where the perturbations
 (x, t)
(x, t)


 M(x, t)
/
M(x, t)
/  M(t) have been decomposed into their
Fourier modes of wavenumber k, and matter is assumed to be
pressureless (always true for the CDM portion and valid for the baryons
on mass scales larger than 105
M
M(t) have been decomposed into their
Fourier modes of wavenumber k, and matter is assumed to be
pressureless (always true for the CDM portion and valid for the baryons
on mass scales larger than 105
M after
photon-baryon
decoupling). Dark energy affects the growth through the "Hubble
damping" term,
2H
after
photon-baryon
decoupling). Dark energy affects the growth through the "Hubble
damping" term,
2H k.
k.
The solution to Eq. (15) is simple to describe during the
three epochs of expansion discussed earlier:
 k
(t) grows as a(t) during the matter-dominated epoch
and is approximately constant during the radiation-dominated and dark
energy-dominated epochs. The key feature here is the fact that once
accelerated expansion begins, the growth of linear perturbations
effectively ends, since the Hubble damping time becomes shorter than the
timescale for perturbation growth.
k
(t) grows as a(t) during the matter-dominated epoch
and is approximately constant during the radiation-dominated and dark
energy-dominated epochs. The key feature here is the fact that once
accelerated expansion begins, the growth of linear perturbations
effectively ends, since the Hubble damping time becomes shorter than the
timescale for perturbation growth.
The impact of the dark energy equation-of-state parameter w on
the growth of structure is more subtle and is illustrated in
Fig. 3. For larger w and fixed
dark energy density
 DE, dark
energy comes to
dominate earlier, causing the growth of linear perturbations to end
earlier; this means the growth factor since decoupling is smaller and
that to achieve the same amplitude by today, the perturbation must begin
with larger amplitude and is larger at all redshifts until today. The
same is true for larger
DE, dark
energy comes to
dominate earlier, causing the growth of linear perturbations to end
earlier; this means the growth factor since decoupling is smaller and
that to achieve the same amplitude by today, the perturbation must begin
with larger amplitude and is larger at all redshifts until today. The
same is true for larger
 DE and fixed
w. Finally, if dark energy is dynamical (not vacuum energy), then
in principle it can be inhomogeneous, an effect ignored above. In
practice, it is expected to be nearly uniform over scales smaller than
the present Hubble radius, in sharp contrast to dark matter, which can
clump on small scales.
DE and fixed
w. Finally, if dark energy is dynamical (not vacuum energy), then
in principle it can be inhomogeneous, an effect ignored above. In
practice, it is expected to be nearly uniform over scales smaller than
the present Hubble radius, in sharp contrast to dark matter, which can
clump on small scales.
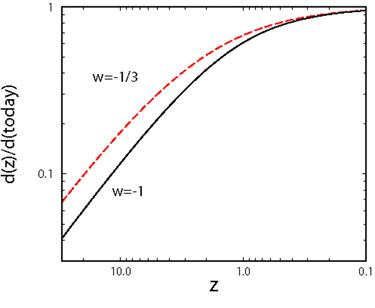 |
Figure 3. Growth of linear density
perturbations in a flat universe with dark energy. Note that the
growth of perturbations ceases when dark energy begins to dominate, 1 +
z =
( |
1 A perfect fluid is fully characterized
by its isotropic pressure p and energy density
 , where
p is a function of density and other state variables (e.g.,
temperature). The equation-of-state parameter w = p /
, where
p is a function of density and other state variables (e.g.,
temperature). The equation-of-state parameter w = p /
 determines the
evolution of the energy density
determines the
evolution of the energy density
 ; e.g.,
; e.g.,

 V1 +
w for constant w, where V is the volume
occupied by the fluid. Vacuum energy or a homogeneous scalar field are
spatially uniform and they too can be fully characterized by
w. The evolution of an inhomogeneous, imperfect fluid is in
general complicated and not fully described by w. Nonetheless, in
the FRW cosmology, spatial homogeneity and isotropy require the
stress-energy to take the perfect fluid form; thus,
w determines the evolution of the energy density.
Back.
V1 +
w for constant w, where V is the volume
occupied by the fluid. Vacuum energy or a homogeneous scalar field are
spatially uniform and they too can be fully characterized by
w. The evolution of an inhomogeneous, imperfect fluid is in
general complicated and not fully described by w. Nonetheless, in
the FRW cosmology, spatial homogeneity and isotropy require the
stress-energy to take the perfect fluid form; thus,
w determines the evolution of the energy density.
Back.