


Although the discovery of cosmic acceleration is often portrayed as a major surprise and a radical contravention of the conventional wisdom, it was anticipated by a number of developments in cosmology in the preceding decade. Moreover, this is not the first time that the cosmological constant has been proposed. Indeed, the cosmological constant was explored from the very beginnings of General Relativity and has been periodically invoked and subsequently cast aside several times since. Here we recount some of this complex 90-year history.
Einstein introduced the cosmological constant in his field equations in
order to obtain a static and finite cosmological solution "as
required by the fact of the small velocities of the stars" and to
be consistent with Mach's principle
[ Einstein 1917].
In Einstein's
solution, space is positively curved, Rcurv =
1 / (4 G
G
 M)1/2, and the
"repulsive gravity" of
M)1/2, and the
"repulsive gravity" of
 is balanced
against the attractive gravity of matter,
is balanced
against the attractive gravity of matter,

 =
=
 M/2.
In the 1920's, Friedmann and Lemaître
independently showed that cosmological solutions with matter and
M/2.
In the 1920's, Friedmann and Lemaître
independently showed that cosmological solutions with matter and
 generally
involved expansion or contraction, and Lemaître as
well as Eddington showed that Einstein's static solution was unstable to
expansion or contraction. In 1917, de Sitter explored a solution in
which
generally
involved expansion or contraction, and Lemaître as
well as Eddington showed that Einstein's static solution was unstable to
expansion or contraction. In 1917, de Sitter explored a solution in
which
 M is
negligible compared to
M is
negligible compared to

 [de Sitter 1917].
There was some early confusion about the
interpretation of this model, but in the early 1920's, Weyl, Eddington,
and others showed that the apparent recession velocity (the redshift) at
small separation would be proportional to the distance,
v = (
[de Sitter 1917].
There was some early confusion about the
interpretation of this model, but in the early 1920's, Weyl, Eddington,
and others showed that the apparent recession velocity (the redshift) at
small separation would be proportional to the distance,
v = ( / 3)1/2 d.
/ 3)1/2 d.
With Hubble's discovery of the expansion of the Universe in 1929,
Einstein's primary justification for introducing the cosmological
constant was lost, and he advocated abandoning it. Gamow later wrote
that Einstein called this "his greatest blunder," since he
could have predicted the expanding Universe. Yet the description above
makes it clear that the history was more complicated, and one could
argue that in fact Friedmann and Lemaître (or de Sitter) had
"predicted" the expanding Universe,
 or no. Indeed,
Hubble noted that his linear relation between redshift and distance was
consistent with the prediction of the de Sitter model
[Hubble 1929].
Moreover, Eddington
recognized that Hubble's value for the expansion rate,
H0
or no. Indeed,
Hubble noted that his linear relation between redshift and distance was
consistent with the prediction of the de Sitter model
[Hubble 1929].
Moreover, Eddington
recognized that Hubble's value for the expansion rate,
H0  570 km/s/Mpc, implied a time back to
the big bang of less than 2 Gyr, uncomfortably short compared to
some age estimates of Earth and the galaxy. By adjusting the
cosmological constant to be slightly larger than the Einstein value,
570 km/s/Mpc, implied a time back to
the big bang of less than 2 Gyr, uncomfortably short compared to
some age estimates of Earth and the galaxy. By adjusting the
cosmological constant to be slightly larger than the Einstein value,

 = (1 +
= (1 +  )
)
 M/2, a
nearly static beginning of arbitrary duration could be obtained, a
solution known as the Eddington-Lemaître model. While Eddington
remained focused on
M/2, a
nearly static beginning of arbitrary duration could be obtained, a
solution known as the Eddington-Lemaître model. While Eddington
remained focused on  ,
trying to find a place for it in his "unified" and "fundamental" theories,
,
trying to find a place for it in his "unified" and "fundamental" theories,
 was no longer the focus of most cosmologists.
was no longer the focus of most cosmologists.
Motivated by the aesthetic beauty of an unchanging Universe, [Bondi & Gold 1948] and [Hoyle 1948] put forth the steady-state cosmology, a revival of the de Sitter model with a new twist. In the steady-state model, the dilution of matter due to expansion is counteracted by postulating the continuous creation of matter (about 1 hydrogen atom/m3/Gyr). However, the model's firm prediction of an unevolving Universe made it easily falsifiable, and the redshift distribution of radio galaxies, the absence of quasars nearby, and the discovery of the cosmic microwave background radiation did so in the early 1960s.
 was briefly
resurrected again in the late 1960s by
[Petrosian,
Salpeter & Szekeres 1967],
who used the Eddington-Lemaître model to explain
the preponderance of quasars at redshifts around z ~ 2. As it
turns out, this is a real observational effect, but it can be attributed
to evolution: quasar activity peaks around this redshift. In 1975,
evidence for a cosmological constant from the Hubble diagram of
brightest-cluster elliptical galaxies was presented
[Gunn &
Tinsley 1975],
though it was realized
[Tinsley &
Gunn 1976]
that uncertainties in galaxy luminosity evolution make
their use as standard candles problematic.
was briefly
resurrected again in the late 1960s by
[Petrosian,
Salpeter & Szekeres 1967],
who used the Eddington-Lemaître model to explain
the preponderance of quasars at redshifts around z ~ 2. As it
turns out, this is a real observational effect, but it can be attributed
to evolution: quasar activity peaks around this redshift. In 1975,
evidence for a cosmological constant from the Hubble diagram of
brightest-cluster elliptical galaxies was presented
[Gunn &
Tinsley 1975],
though it was realized
[Tinsley &
Gunn 1976]
that uncertainties in galaxy luminosity evolution make
their use as standard candles problematic.
While cosmologists periodically hauled the cosmological constant out of
the closet as needed and then stuffed it back in, in the 1960s
physicists began to understand that
 cannot be treated
in such
cavalier fashion. With the rise of the standard big-bang cosmology came
the awareness that the cosmological constant could be a big problem
[Zel'dovich
1968].
It was realized that the energy density of the quantum vacuum should
result in a cosmological constant of enormous size (see
Section 5.1.1). However, because of
the success of the hot
big-bang model, the lack of compelling ideas to solve the cosmological
constant problem, and the dynamical unimportance of
cannot be treated
in such
cavalier fashion. With the rise of the standard big-bang cosmology came
the awareness that the cosmological constant could be a big problem
[Zel'dovich
1968].
It was realized that the energy density of the quantum vacuum should
result in a cosmological constant of enormous size (see
Section 5.1.1). However, because of
the success of the hot
big-bang model, the lack of compelling ideas to solve the cosmological
constant problem, and the dynamical unimportance of
 at the
early epochs when the hot big-bang model was best tested by big-bang
nucleosynthesis and the CMB, the problem was largely ignored in
cosmological discourse.
at the
early epochs when the hot big-bang model was best tested by big-bang
nucleosynthesis and the CMB, the problem was largely ignored in
cosmological discourse.
In the early 1980s the inflationary universe scenario
[Guth 1981],
with its predictions of a spatially flat Universe
( = 1) and
almost-scale-invariant density
perturbations, changed the cosmological landscape and helped set the
stage for the discovery of cosmic acceleration. When inflation was
first introduced, the evidence for dark matter was still accruing, and
estimates of the total matter density, then about
= 1) and
almost-scale-invariant density
perturbations, changed the cosmological landscape and helped set the
stage for the discovery of cosmic acceleration. When inflation was
first introduced, the evidence for dark matter was still accruing, and
estimates of the total matter density, then about
 M ~ 0.1,
were sufficiently uncertain that an
Einstein-de Sitter model (i.e.,
M ~ 0.1,
were sufficiently uncertain that an
Einstein-de Sitter model (i.e.,
 M = 1)
was not ruled out. The evidence for a low value of
M = 1)
was not ruled out. The evidence for a low value of
 M
was, however, sufficiently worrisome that the need for a smooth
component, such as vacuum energy, to make up the difference for a flat
Universe was suggested
[Peebles 1984,
Turner, Steigman
& Krauss 1984].
Later, the model for large-scale structure formation
with a cosmological constant and cold dark matter
(
M
was, however, sufficiently worrisome that the need for a smooth
component, such as vacuum energy, to make up the difference for a flat
Universe was suggested
[Peebles 1984,
Turner, Steigman
& Krauss 1984].
Later, the model for large-scale structure formation
with a cosmological constant and cold dark matter
( CDM) and the
spectrum of density perturbations predicted by inflation was found to
provide a better fit (than
CDM) and the
spectrum of density perturbations predicted by inflation was found to
provide a better fit (than
 M = 1) to
the growing observations of large-scale structure
[Turner 1991,
Efstathiou,
Sutherland & Maddox 1990].
The 1992 COBE discovery of CMB anisotropy provided
the normalization of the spectrum of density perturbations and drove a
spike into the heart of the
M = 1) to
the growing observations of large-scale structure
[Turner 1991,
Efstathiou,
Sutherland & Maddox 1990].
The 1992 COBE discovery of CMB anisotropy provided
the normalization of the spectrum of density perturbations and drove a
spike into the heart of the
 M = 1 CDM
model.
M = 1 CDM
model.
Another important thread involved age consistency. While estimates of
the Hubble parameter had ranged between 50 and 100 km/s/Mpc since the
1970s, by the mid-1990s they were settling out in the middle of that
range. Estimates of old globular cluster ages had similar swings, but
had settled at t0
 13-15 Gyr. The
resulting expansion age, H0 t0 =
(H0 / 70km/s/Mpc)(t0 / 14 Gyr)
was uncomfortably high compared to that for the Einstein-de Sitter
model, for which H0 t0 = 2/3. The
cosmological constant offered a ready solution, as the age of a flat
Universe with
13-15 Gyr. The
resulting expansion age, H0 t0 =
(H0 / 70km/s/Mpc)(t0 / 14 Gyr)
was uncomfortably high compared to that for the Einstein-de Sitter
model, for which H0 t0 = 2/3. The
cosmological constant offered a ready solution, as the age of a flat
Universe with  rises with
rises with 
 ,
,
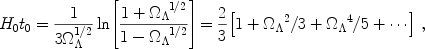 |
(16) |
reaching H0 t0
 1 for
1 for

 =
0.75.
=
0.75.
By 1995 the cosmological constant was back out of the cosmologists'
closet in full glory
[Krauss &
Turner 1995,
Ostriker &
Steinhardt 1995,
Frieman et
al. 1995]:
it solved the age problem, was consistent with growing evidence that
 M was
around 0.3, and fit the growing body of observations of large-scale
structure. Its only serious competitors were "open
inflation," which had a small group of adherents, and hot + cold
dark matter, with a low value for the Hubble parameter (~
50 km/s/Mpc) and neutrinos accounting for 10% to 15% of the dark
matter (see, e.g., contributions in
[Turok
1997]).
During this period, there were two results that conflicted with
M was
around 0.3, and fit the growing body of observations of large-scale
structure. Its only serious competitors were "open
inflation," which had a small group of adherents, and hot + cold
dark matter, with a low value for the Hubble parameter (~
50 km/s/Mpc) and neutrinos accounting for 10% to 15% of the dark
matter (see, e.g., contributions in
[Turok
1997]).
During this period, there were two results that conflicted with
 CDM:
analysis of the statistics of lensed quasars
[Kochanek 1996]
and of the first 7
high-redshift supernovae of the Supernova Cosmology Project
[Perlmutter et
al. 1997]
respectively indicated that
CDM:
analysis of the statistics of lensed quasars
[Kochanek 1996]
and of the first 7
high-redshift supernovae of the Supernova Cosmology Project
[Perlmutter et
al. 1997]
respectively indicated that

 < 0.66 and
< 0.66 and

 < 0.51 at 95% confidence, for a flat
Universe. The discovery of accelerated expansion in 1998 saved inflation
by providing evidence for large
< 0.51 at 95% confidence, for a flat
Universe. The discovery of accelerated expansion in 1998 saved inflation
by providing evidence for large

 and
was thus welcome news for cosmology.
and
was thus welcome news for cosmology.
Two breakthroughs enabled the discovery of cosmic acceleration. The first was the demonstration that type Ia supernovae (SNe Ia) are standardizable candles [Phillips 1993]. The second was the deployment of large mosaic CCD cameras on 4-meter class telescopes, enabling the systematic search of large areas of sky, containing thousands of galaxies, for these rare events. By comparing deep, wide images taken weeks apart, the discovery of SNe at redshifts z ~ 0.5 could be "scheduled" on a statistical basis.
Two teams, the Supernova Cosmology Project and the High-z SN Search,
working independently in the mid- to late-1990s took advantage of these
breakthroughs to measure the SN Hubble diagram to much larger distances
than was previously possible. Both teams found that distant SNe are
~ 0.25 mag dimmer than they would be in a decelerating Universe,
indicating that the expansion has been speeding up for the past 5 Gyr
[Riess et al. 1998,
Perlmutter et
al. 1999];
see Fig. 4. When
analyzed assuming a Universe with matter and cosmological constant,
their results provided evidence for

 > 0 at greater than 99% confidence (see Fig. 8 for the
current constraints).
> 0 at greater than 99% confidence (see Fig. 8 for the
current constraints).
 |
Figure 4. Discovery data: Hubble diagram of
SNe Ia measured by the Supernova Cosmology Project and the High-z
Supernova Team. Bottom panel shows residuals in distance modulus
relative to an open universe with
|