One of the first things one learns in cosmology is that geometry is
destiny: a closed (positively curved) Universe eventually recollapses,
and an open (flat or negatively curved) Universe expands
forever. Provided the Universe contains only matter and
= 0, this follows
directly from Eq. (2).
The presence of dark energy severs this well known connection between
geometry and destiny and raises fundamental issues involving the distant
future of our Universe
[Krauss &
Turner 1995].
To illustrate the geometry-destiny connection, we can rewrite Eq. (2) in terms of an effective potential and a kinetic-energy term,
 |
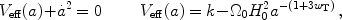(34) |
where wT is the ratio of the total pressure to
the total energy density (including all components). If
wT > -1/3, as would be the case with
only matter and radiation, then the second term in
Veff increases monotonically from
-
to 0 as a
goes from 0 to
, which means that
Veff rises from
- to k. For
k > 0, there is a value of a where
Veff
0, at which point
must go
to zero and a achieves its maximum value. For k = 0,
only vanishes for
a
; and for k
< 0,
remains positive even
as a
.
With dark energy there is a new twist: since the dark energy density
decreases more slowly than that of matter or radiation, as the Universe
expands dark energy eventually dominates the second term in
Veff. Thereafter, Veff
decreases monotonically, since wT
wDE < -1/3, approaching
-
as a
. Provided that
DE
> 0 and that wDE remains negative, if the scale
factor becomes large enough for dark energy to dominate, which happens
unless 
M
>1 ≫
DE, then
the Universe will expand forever, irrespective of k.
If dark energy is vacuum energy, acceleration will continue, and the expansion will become exponential, leading to a "red out" of the Universe. To see this, consider the comoving distance to fixed redshift z at time t during the epoch of exponential expansion:
 |
(35) |
The exponential decrease of this distance implies that the number of
galaxies below a fixed redshift shrinks exponentially. By contrast, in
the Einstein-de Sitter model with
M = 1, this
distance increases as t1/3, so that the number of
galaxies with redshift less than a fixed value grows slowly.
Alternatively, Eq. 35 implies that the
redshift for a galaxy at current distance r grows exponentially.
Galaxies beyond the Local Group, r
1-2 Mpc, will be
redshifted beyond detectability on a timescale of
t - t0 ~ 100 Gyr (e.g.,
[Busha et al. 2003]).
The Milky Way will remain gravitationally bound to
the Local Group, which will appear as a static, "island
Universe." Even the CMB, the other key evidence of a once-hot,
expanding Universe, will be redshifted to undetectability
[Krauss
& Scherrer 2007].
If dark energy is a scalar field, then eventually the field relaxes to
the minimum of its potential; see
Fig. 10. If the minimum of the
potential energy is precisely zero, the Universe will again become
matter dominated and return to decelerated expansion, restoring the link
between geometry and destiny. If the minimum of the scalar field
potential has negative energy density, the energy of dark matter and of
scalar field energy will eventually cancel, leading to recollapse,
irrespective of k. If the potential energy at the minimum is
positive and larger than a critical value that depends on
M (the
critical value is zero for
M ≤
1 and small for
M >
1), then accelerated expansion will
eventually ensue again and as discussed above, the Universe will
experience a "red-out." These possibilities are illustrated
in Fig. 18.
 |
Figure 18. Evolution of the FRW scale
factor in models with and without dark energy. Upper four curves are
for flat models. Dashed curves denote models with w = -0.8 or
-1.2 and
|
Finally, the possibility of wDE < -1
deserves special comment. In this case, the energy density of dark
energy actually increases with time,
DE
a
, where
-3(1 + w)
> 0. In turn, the scale factor grows very rapidly and reaches
infinite size in a finite time:
 |
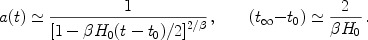(36) |
This is the "big rip" scenario of [Caldwell, Kamionkowski & Weinberg 2003]. Once the density of dark energy exceeds that of any structure - from clusters to atoms - that structure is torn apart.
The presence of dark energy severs the simple relation between geometry and destiny, links destiny to an understanding of dark energy, raises the specter of a bleak future for cosmologists, and raises a deep question [Krauss & Turner 1995]: can we ever determine the future of the Universe with certainty? As a thought experiment, ignore the current epoch of accelerated expansion and imagine instead that the Universe has been determined to be matter dominated and that it is flat. We might be tempted to conclude that the Universe will expand forever at an ever-decreasing rate. However, no matter how precise our measurements are, there could be a small cosmological constant lurking below the threshold of detectability. For example, if the vacuum energy density were one billionth of the present matter density, after a factor of 1000 in expansion vacuum energy would come to dominate. If it were positive, exponential expansion would eventually ensue; if negative, the Universe would ultimately recollapse. Only a fundamental understanding of the constituents of the Universe and their relative abundances could deliver certainty about the destiny of the Universe.